1.1節 可測空間と測度
著者:梅谷 武
語句:σ-加法族,可測空間,測度,確率測度,測度空間,Borel σ-加法族,Borel集合,Borel測度,完備,完備化
一般の集合上に測度を定義し、その性質について述べる。また、位相空間上の測度、ℝd上のBorel測度、測度の完備性、実数のコンパクト化について述べる。
作成:2011-12-08
更新:2012-02-15
集合
Ωの部分集合族
が
Ω上の
σ-加法族しぐまかほうぞく, σ-algebraであるとは、次の条件を満たすことである。
| (σ.1)
| ∅, Ω ∈ |
| (σ.2)
| A ∈ ⇒ Ac ∈ |
| (σ.3)
| An ∈ , n = 1,2,⋯ ⇒ ∪n An ∈ |
可測空間
(Ω,)上の
測度そくど, measureとは、次の性質を満たす
上の関数
μ: → ℝ∪{∞}のことである。
| (m.1)
| 0 ≦ μ(A) ≦ ∞, A ∈ |
| (m.2)
| An ∈ , n = 1,2,⋯, An ∩ Am = ∅
(n ≠ m) ⇒ μ( ∪n An ) = ∑n μ( An ) |
測度
Pがさらに次の性質を満たすとき
確率測度かくりつそくど, probability measureという。
| (m.1')
| 0 ≦ P(A) ≦ 1, A ∈ |
| (m.3)
| P(Ω) = 1 |
一般に集合列
{Ak}, k∈ℕに対して、その上極限と下極限を次のように定義する。
集合列
{Ak}, k∈ℕの上極限と下極限について、次が成り立つ。
| (ⅰ)
| a ∈ limsupk→∞Ak ⇔ aは無限個のAkに含まれる。
|
| (ⅱ)
| a ∈ liminfk→∞Ak ⇔ aは有限個を除くすべてのAkに含まれる。
|
| (ⅲ)
| liminfk→∞Ak ⊂ limsupk→∞Ak |
証明
演習とする。■
liminfk→∞Ak = limsupk→∞Akのとき集合列
{Ak}は収束するといい、次のように書く。
集合
Ω上のσ-加法族
の集合列
An ∈ , n = 1,2,⋯において次が成り立つ。
| (σ.4)
| ∩n An ∈ |
| (σ.5)
| limsupk→∞Ak ∈ |
| (σ.6)
| liminfk→∞Ak ∈ |
証明
演習とする。■
可測空間
(Ω,)上の測度
μには次の性質がある。
A,B ∈ , An ∈ , n = 1,2,⋯| (m.4)
| μ(∅) = 0 |
| (m.5)
| A ⊂ B ⇒ μ(A) ≦ μ(B) |
| (m.6)
| μ(A ∪ B) = μ(A) + μ(B) － μ(A ∩ B) |
| (m.7)
| μ( ∪n An ) ≦ ∑n μ( An ) |
| (m.8)
| A1 ⊂ A2 ⊂ ⋯ ⊂ An ⊂ ⋯ ⇒ μ( ∪n An ) = limn→∞ μ( An ) |
| (m.9)
| μ(A1) ＜ ∞, A1 ⊃ A2 ⊃ ⋯ ⊃ An ⊃ ⋯ ⇒ μ( ∩nAn ) = limn→∞ μ( An ) |
証明
演習とする。■
測度空間
(Ω,,μ)上の集合列
An ∈ , n = 1,2,⋯において、
μ( ∪n An ) ＜ ∞ならば
証明
演習とする。■
測度空間
(Ω,,μ)上の集合列
An ∈ , n = 1,2,⋯において、
証明
演習とする。■
集合
Ωの部分集合族
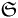
が与えられたとき、
とおくと、
σ[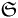]は
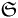
を含む最小のσ-加法族となる。
証明
演習とする。■
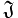 d ≡ { (a1,b1) × ⋯ × (ad,bd] の有限和 |
－∞ ≦ ak ≦ bk ≦ ∞, k = 1,⋯,d }
|
は
ℝdのBorel集合
d ≡ (ℝd)を生成する。但し、
(an,∞]は
(an,∞)と置き換える。
証明
演習とする。■
(ℝd,d)上の測度は
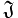d上で一致すれば等しい。
証明
演習とする。■
測度空間
(Ω,,μ)において
| = { A ⊂ Ω | B1 ⊂ A ⊂ B2,
μ(B2－B1) = 0, ∃ B1, B2 ∈ }
|
| μ(A) = μ(B1), A ∈
|
とすると
(Ω,,μ)は完備な測度空間となる。
ここで、
⊂ であり、
μは
上で
μに一致する。
証明
演習とする。■
ℝ = ℝ∪{±∞}に次のような演算を定義する。
a∈ℝ, a ＞ 0のとき
この演算はℝ値関数の和・差・積を定義するための形式的なものであり、これによりℝを代数系として扱うわけではない。
ℝは(0,1)と同相であり、ℝにはその同相写像を拡張し[0,1]と同相になるような位相を入れる。これにより、ℝはコンパクト位相空間となる。
数 学
σ-加法族 しぐまかほうぞく, σ-algebra
可測空間 かそくくうかん, measurable space
測度 そくど, measure
確率測度 かくりつそくど, probability measure
測度空間 そくどくうかん, measure space
Borel σ-加法族 ぼれるしぐまかほうぞく, Borel σ-algebra
Borel集合 ぼれるしゅうごう, Borel set
Borel測度 ぼれるそくど, Borel measure
完備 かんび, complete
完備化 かんびか, completion
| 
とする。このとき、