5.5節 χ2分布
著者:梅谷 武
語句:χ2分布
χ2分布について述べる。
作成:2012-02-18
更新:2012-02-26
5.5 χ2分布
5.5.1 分布
 a = n/2, b = 2, n ∈ ℕとするときのΓ分布
χ2(n) ≡ Γlb48
n
2
, 2 rb48,  n ∈ ℕ
を自由度nのχ2分布かいじじょうぶんぷ, χ2 distributionという。

密度関数

fn(x) ≡ lc96
1
2n/2Γ(n/2)
xn/2－1e－x/2,
x
＞
0
0,
x
≦
0
5.5.2 平均と分散

平均

m = n

分散

σ2 = 2n
5.5.3 積率母関数
 χ2分布χ(n)に従う確率変数Xの積率母関数を求める。
α ≡
n
2
,  β ≡
1
2
とおく。
MX(t)
=
1
2αΓ(α)
∫∞
 
0
e－(β－t)xxα－1dx
=
1
2αΓ(α)(β－t)α－1
∫∞
 
0
e－(β－t)x{(β－t)x}α－1dx
ここでy ≡ (β－t)xとおくと、x = y/(β－t)であり、
MX(t)
=
1
2αΓ(α)(β－t)α
∫∞
 
0
e－yyα－1dy
=
1
2α(β－t)α
 = (2β－2t)－α = (1－2t)－n/2

積率母関数

MX(t) = (1－2t)－n/2
5.5.4 再生性

定理5.5.4.1 χ2分布の再生性

 独立な確率変数X, Yがそれぞれχ2分布χ2(n1), χ2(n2)に従っているとき、それらの和Z ≡ X + Yはχ2分布χ2(n1+n2)に従う。

証明

MZ(t) = MX(t)MY(t) = (1－2t)－(n1+n2)/2
■
5.5.5 正規分布の平方和

補題5.5.5.1

 確率変数Xが標準正規分布N(0,1)に従うとき、確率変数Y = X2はχ2分布χ2(1)に従う。

証明

 μXは次の密度関数f(x)をもつ。
f(x) =
1
√2π
exp lb48 －
x2
2
 rb48
P(Y ≦ y) = P(－√y ≦ x ≦ √y)より、
P(Y ≦ y) =
∫√y
 
－√y
f(x)dx
 = 2
∫√y
 
0
f(x)dx
ここで変数変換y = x2を行なう。y ≧ 0でx = √yを逆関数としてもつから、
P(Y ≦ y) =
∫y
 
0
f(√y)y－1/2dy
となり、確率変数Yは次の密度関数g(y)をもつ。
g(y) =
1
√2π
e－y/2y－1/2
ここで、変数変換x = t2により
Γlb48
1
2
 rb48 =
∫∞
 
0
x－1/2e－xdx
 = 2
∫∞
 
0
e－t2dt
 = √π
よってg(y)はΓ(1/2,2)すなわちχ2(1)の密度関数である。
g(y) =
1
21/2Γ(1/2)
y－1/2e－y/2
■

定理5.5.5.3 正規分布の平方和

 独立な確率変数Xi, i = 1,⋯,nがそれぞれ正規分布N(mi,σi2)に従っているとき、それらを標準化した平方和
Y =
n
∑
i = 1
(Xi－mi)2
σi2
は自由度nのχ2分布χ2(n)に従う。

証明

Xi－mi
σi
,  i = 1,⋯,n
が標準正規分布N(0,1)に従うこととχ2分布の再生性より。■
5.5.6 グラフ

graph008.r

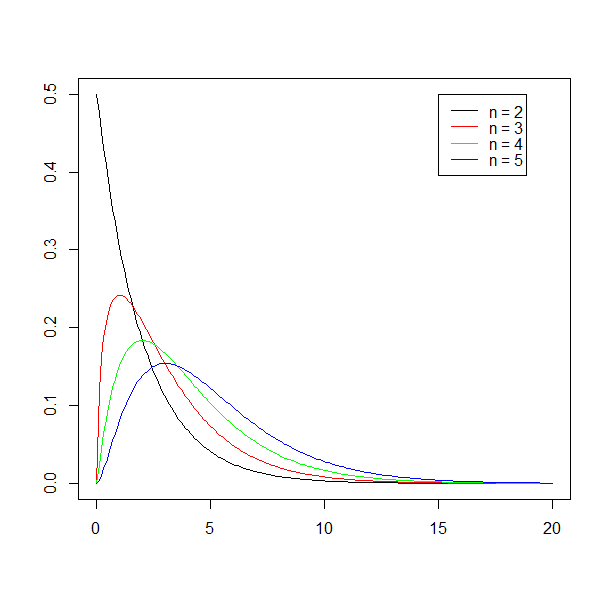
 χ2(n), n = 2, 3, 4, 5を描く。
x <- seq( 0, 20, 0.1 )
plot( x, dchisq( x, 2, log=FALSE ),
  type="l", xlab="", ylab="" )
points( x, dchisq( x, 3, log=FALSE ), type="l", col="red" )
points( x, dchisq( x, 4, log=FALSE ), type="l", col="green" )
points( x, dchisq( x, 5, log=FALSE ), type="l", col="blue" )
legend( 15, 0.5,
  legend = c( "n = 2", "n = 3", "n = 4", "n = 5" ),
  col = c("black","red","green","blue"),
  lty = 1 )
図5.5.6.4 χ2分布
χ<sup>2</sup>分布
数　　学
χ2分布 かいじじょうぶんぷ, χ2 distribution