3.2節 独立性
著者:梅谷 武
語句:独立,畳み込み
事象の独立性と確率変数の独立性についてまとめる。確率測度の畳み込みについて述べる。
作成:2012-01-16
更新:2012-02-19
確率空間
(Ω, ,P)
,P)上の有限事象列
{A1, ⋯, An},
Ai∈
が
独立どくりつ, independentであるとは、任意の
1≦i1<⋯<ik≦n, k≧2について次が成り立つことである。
| P(Ai1 ∩ ⋯ ∩ Aik) = P(Ai1) ⋯ P(Aik)
|
無限事象族
{Aλ}λ∈Λ, Aλ∈
の独立性については、その任意の有限部分族が独立であることと定義する。
確率空間
(Ω, ,P)
,P)上の独立な有限事象列
{A1, ⋯, An},
Ai∈
について、
i = 1, ⋯ nに対して
Bi = Aiまたは
Aicとおけば
{B1, ⋯, Bn}も独立である。
証明
演習とする。■
確率空間
(Ω, ,P)
,P)上の独立な事象列
{An}n∈ℕについて、次が成り立つ。
P 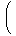 | | 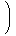 = =
| |
|
証明
演習とする。■
確率空間
(Ω, ,P)
,P)上の事象列
{An}n∈ℕが独立であれば、
証明
演習とする。■
確率空間
(Ω, ,P)
,P)上の有限確率変数列
{X1, ⋯, Xn}が
独立どくりつ, independentであるとは、可測関数としての値域における任意の事象の組
A1, ⋯, Anについて次が成り立つことである。
| P(X1 ∈ A1, ⋯, Xn ∈ An) =
P(X1 ∈ A1) ⋯ P(Xn ∈ An)
|
無限確率変数族
{Xλ}λ∈Λの独立性については、その任意の有限部分族が独立であることと定義する。
確率空間
(Ω, ,P)
,P)上の可測空間
(S,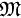 )
)を値域とする確率変数
Xについて
σ(X) ≡ { X-1(A) ∈  | A ∈ | A ∈ 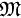 } }
|
は

の部分σ-加法族となる。したがって、確率変数族
{Xλ}を与えれば、それから部分σ-加法族の族
{σ(Xλ)}が定まり、確率変数族の独立性は、その部分σ-加法族の族から任意に選んだ事象族の独立性と同等の概念になっている。
確率空間
(Ω, ,P)
,P)上の事象列
{An}n∈ℕが独立であるための必要十分条件は確率変数列
{1An}n∈ℕが独立であることである。
証明
演習とする。■
確率空間
(Ω, ,P)
,P)上の確率変数列
{X1, ⋯, Xn}が独立であるための必要十分条件は結合分布
X = (X1, ⋯, Xn)について、次が成り立つことである。
証明
演習とする。■
確率空間
(Ω, ,P)
,P)上の独立確率変数列
{X1, ⋯, Xn}と任意の
(ℝ, 1)
1)上の実可測関数列
{f1, ⋯, fn}について、それらの合成
{f1(X1), ⋯, fn(Xn)}は独立確率変数列となる。
証明
演習とする。■
確率空間
(Ω, ,P)
,P)上の可積分な確率変数列
{X1, ⋯, Xn}が独立であるための必要十分条件は任意の
(ℝ, 1)
1)上の有界な実可測関数列
{f1, ⋯, fn}について、次が成り立つことである。
| E[f1(X1)⋯fn(Xn)] = E[f1(X1)]⋯E[fn(Xn)]
|
証明
演習とする。■
二乗可積分な独立確率変数列
{X1, ⋯, Xn}について次が成り立つ。
V 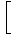 | | 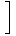 = = | |
|
証明
演習とする。■
| μ*ν(E) = | | | , E ∈  1 1
|
証明
演習とする。■
証明
演習とする。■
可測空間
(ℝ, 1)
1)上の確率測度
μ1,μ2,μ3について次が成り立つ。
| (ⅰ)
| μ1*μ2 = μ2*μ1 |
| (ⅱ)
| (μ1*μ2)*μ3 = μ1*(μ2*μ3) |
証明
演習とする。■
確率空間
(Ω, ,P)
,P)上の独立な確率変数
X,Yについて次が成り立つ。
証明
演習とする。■
数 学
独立 どくりつ, independent
独立 どくりつ, independent
畳み込み たたみこみ, convolution
 ,P)上の可測空間(S,
,P)上の可測空間(S,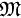 )を値域とする確率変数Xについて
)を値域とする確率変数Xについて
 の部分σ-加法族となる。したがって、確率変数族{Xλ}を与えれば、それから部分σ-加法族の族{σ(Xλ)}が定まり、確率変数族の独立性は、その部分σ-加法族の族から任意に選んだ事象族の独立性と同等の概念になっている。
の部分σ-加法族となる。したがって、確率変数族{Xλ}を与えれば、それから部分σ-加法族の族{σ(Xλ)}が定まり、確率変数族の独立性は、その部分σ-加法族の族から任意に選んだ事象族の独立性と同等の概念になっている。