2.2節 Starlingの公式

著者:梅谷武
語句:部分積,無限乗積,広義一様収束,ζ関数,Γ関数,Β関数,Gaussの公式,Weierstrassの公式,Eulerの定数,二重階乗,Wallisの公式,Starlingの公式

無限乗積を定義し、その収束性について述べる。関数を無限級数でなく無限乗積で表現した方が都合がいいときがある。関数項級数の収束判定のためのWeierstrassのM-判定法とその応用例としてRiemannのζ関数の収束性について述べる。Bernoulli数、Bernoulli多項式、ζ関数はさまざまな局面に現れる。Γ関数とΒ関数を定義し、その性質をまとめる。最後にEuler-Maclaurinの公式を使ってStarlingの公式を証明する。

作成:2012-01-17
更新:2021-04-03

2.2 Starlingの公式

2.2.1 無限乗積

定義2.2.1.1 無限乗積

複素数列{a_n}_n∈ℕの各項が0でないとき、部分積ぶぶんせき, partial product

p_n ≡

n
∏
i = 1

a_n

がn → ∞で0でない複素数pに収束するとき、無限乗積むげんじょうせき, infinite product

∞
∏
i = 1

a_n

はpに収束するという。有限個の項が0のとき、それらを取り除いたときに収束するときにその無限乗積は0に収束するという。

すべての項が0でない無限乗積に関するCauchyの収束条件は

∀ ε ＞ 0, ∃ N ∈ ℕ：m ＞ n ≧ N ⇒

p_m － p_n

p_n

a_n+1⋯a_m － 1

＜ ε

となり、{p_n}は有界であるから、a_n → 1 (n → ∞)となることがわかる。このことから無限乗積を

∞
∏
i = 1

(1 + a_n)

lim
n → ∞

a_n

= 0

という標準形にして考えることができる。

補題2.2.1.3

各項a_nが正の実数であるとき、

∞
∏
n = 1

(1 + a_n)

＜ ∞ ⇔

∞
∑
n = 1

a_n

＜ ∞

証明

a_n＞0より

1 ＜ 1 + a_n ＜ e^a_n

したがって、

1 +

N
∑
n = 1

a_n

＜

N
∏
n = 1

(1 + a_n)

＜

N
∏
n = 1

exp(a_n)

= exp

N
∑
n = 1

a_n

■

補題2.2.1.5

各項a_nが1 ＞ a_n ＞ 0を満たすとき

∞
∏
n = 1

(1 － a_n)

＜ ∞ ⇔

∞
∑
n = 1

a_n

＜ ∞

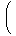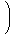
証明

級数が発散するとき、

N
∏
n = 1

(1 － a_n)

＜ exp

－

N
∑
n = 1

a_n

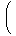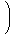
より、部分積が0に収束するので無限乗積は0に発散する。
級数が収束するときは、部分和が減少列であるから、下から押さえられることを示せばよい。あるNが存在して

a_n ＜

, n ≧ N

となる。このとき次が成り立つ。

1 + 2 a_n

≦ 1 － a_n, n ≧ N

級数が収束することから

N
∑
n = 1

a_n

N
∑
n = 1

2 a_n

も収束し、したがって

∞
∏
n = 1

(1 + 2 a_n)

も収束する。ゆえに部分積には下限があり、収束する。■

命題2.2.1.7

無限乗積

∞
∏
n = 1

(1 +

a_n

)

が収束すれば

∞
∏
n = 1

(1 + a_n)

も収束する。

証明

(1+a_n+1)⋯(1+a_m) － 1

≦ (1+

a_n+1

)⋯(1+

a_m

) － 1

よりCauchyの収束条件が満たされる。■

定義2.2.1.9 絶対収束

無限乗積

∞
∏
n = 1

(1 + a_n)

が絶対収束するとは、無限乗積

∞
∏
n = 1

(1 +

a_n

)

が収束することである。

命題2.2.1.10

無限乗積

∞
∏
n = 1

(1 + a_n)

が絶対収束することと、無限級数

∞
∑
n = 1

a_n

が絶対収束することは同値である。

証明

補題1.8.1.3より。■

2.2.2 WeierstrassのM-判定法

定理2.2.2.1 Weierstrass

複素領域D上の正則関数列{f_n(z)}_n∈ℕがD上で優級数

f_n(z)

≦ M_n, z ∈ D,

∞
∑
n = 1

M_n

＜ ∞

をもつとき、無限級数

f(z) ≡

∞
∑
n = 1

f_n(z)

はD上で一様収束し、正則関数となる。さらにこのとき項別微分可能である。

f^(k)(z) =

∞
∑
n = 1

f_n^(k)(z)

, k = 1,2,⋯

証明

演習とする。■

系2.2.2.3 Riemannのζ関数

ζ(s) ≡

∞
∑
n = 1

n^s

は、右半平面{ s ∈ ℂ | Re(s) ＞ 1 }において広義一様収束こうぎいちようしゅうそく, uniform convergence in the wider sense ^*1し、正則関数となる。

証明

r ＞ 1, M_n = n^-rとすると

n^－s

= n^－Re(s) ≦ M_n, Re(s) ≧ r,

∞
∑
n = 1

M_n

＜ ∞

したがって、ζ(s)は{ s ∈ ℂ | Re(s) ≧ r }で一様収束する。■

この関数は全平面上に拡張することができて、Riemannのζ関数ぜーたかんすう, ζ functionと呼ばれる。Bernoulli数はζ関数の負の整数点での値と次のような関係がある。

定理2.2.2.6

ζ関数は全平面に解析接続され、s ≠ 1で正則であり、次が成り立つ。

ζ( 1 － k ) = －

B_k

, k ∈ ℕ

証明

Euler-Maclaurinの公式を使って証明することができる。■

定理2.2.2.8

複素領域D上の正則関数列{f_n(z)}_n∈ℕがD上で優級数

f_n(z)

≦ M_n, z ∈ D,

∞
∑
n = 1

M_n

＜ ∞

をもつとき、無限乗積

f(z) ≡

∞
∏
n = 1

(1 + f_n(z))

はD上で一様収束し、正則関数となる。さらにこのとき次が成り立つ。

(ⅰ)

f(z) = 0 ⇔ ∃ n ∈ ℕ：1 + f_n(z) = 0

(ⅱ)

f'(z)

f(z)

∞
∑
n = 1

f_n'(z)

1 + f_n(z)

証明

演習とする。■

2.2.3 Γ関数とΒ関数

定理2.2.3.1 Γ関数

広義積分

Γ(x) ≡

∫

∞

0

e^－tt^x－1dt

, x ＞ 0

は収束する。これを(0,∞)上の関数と考えたものをΓ関数がんまかんすう, Γ functionという。

証明

演習とする。■

定理2.2.3.3 Β関数

広義積分

Β(x,y) ≡

∫

1

0

t^x－1(1－t)^y－1dt

, x,y ＞ 0

は収束する。これを(0,∞)×(0,∞)上の関数と考えたものをΒ関数べーたかんすう, Β functionという。

証明

演習とする。■

命題2.2.3.5

Γ関数はx ＞ 0でC^∞級であり、次が成り立つ。

Γ⁽ⁿ⁾(x) =

∫

∞

0

e^－tt^x－1(log t)ⁿdt

, x ＞ 0, n ∈ ℕ

証明

演習とする。■

命題2.2.3.7

x ＞ 0, n ∈ ℕについて次が成り立つ。

(ⅰ)	Γ(x) ＞ 0
(ⅱ)	Γ(x + 1) = xΓ(x)
(ⅲ)	Γ(1) = 1
(ⅳ)	Γ(n + 1) = n!

証明

演習とする。■

命題2.2.3.9

x,y ＞ 0について次が成り立つ。

B(x,y) =

Γ(x)Γ(y)

Γ(x + y)

証明

演習とする。■

命題2.2.3.11 Gaussの公式

Γ(x) =

lim
n → ∞

n! n^x

x(x+1)⋯(x+n)

, x ＞ 0

証明

演習とする。■

Gaussの公式がうすのこうしき, Gauss's formulaの右辺はD ≡ { x∈ℝ | x ≠ －n, n ∈ ℕ }で収束することから、Γ関数の定義域をこの集合まで拡張する。

Γ(x) ≡

lim
n → ∞

n! n^x

x(x+1)⋯(x+n)

, x ∈ { x∈ℝ | x ≠ －n, n ∈ ℕ }

ここでΓ(x) ≠ 0であり、

lim
x → －n

Γ(x)

= 0, n ∈ ℕ

が成り立つことから、1/Γ(x)をℝ上連続となるように拡張する。これを無限乗積に展開するのがWeierstrassの公式わいえるしゅとらすのこうしき, Weierstrass's formulaである。

命題2.2.3.14 Weierstrassの公式

Γ(x)

= xe^γx

∞
∏
n = 1

1 +

e^－x/n

, x ∈ ℝ

ここでγはEulerの定数おいらーのていすう, Euler's constantである。

γ ≡

lim
n → ∞

1 +

+ ⋯ +

－ log n

証明

演習とする。■

命題2.2.3.16

(ⅰ)

x+1

= 2^1－x√πΓ(x), x ∈ D

(ⅱ)

Γ(x)Γ(1－x)

sin πx

, x ∈ ℝ

(ⅲ)

sin πx = πx

∞
∏
n = 1

1 －

x²

n²

, x ∈ ℝ

証明

演習とする。■

二重階乗にじゅうかいじょう, double factorialはn ∈ ℕについて次のように定義される。

(2n－1)!! ≡

n
∏
k = 1

( 2k － 1 )

(2n)!

n!2ⁿ

(2n)!! ≡

n
∏
k = 1

= n!2ⁿ

次のWallisの公式うぉりすのこうしき, Wallis's formulaはStarlingの公式における定数を確定するために用いられる。

系2.2.3.19 Wallisの公式

(ⅰ)

∞
∏
n = 1

1 －

4n²

(ⅱ)

lim
n → ∞

2²ⁿ(n!)²

(2n)!√n

lim
n → ∞

(2n)!!

(2n－1)!!√n

= √π

証明

演習とする。■

2.2.4 Starlingの公式

Starlingの公式すたーりんぐのこうしき, Starling's formulaは中心極限定理の原型であるde Moivre-Laplaceの定理の証明に用いられる。多くの証明法が知られているが、ここでは和の漸近近似式の導出に便利なEuler-Maclaurinの公式を使う。

定理2.2.4.2 Γ関数形

Γ(x) ∼ √2πx^x－1/2e^－x, (x → ∞)

証明

Gaussの公式を使ってlogΓ(x)を展開する。

log Γ(x)

log (x－1)Γ(x－1)

log (x－1)

lim
n → ∞

n! n^x－1

(x－1)x(x+1)⋯(x+n－1)

lim
n → ∞

log

n! n^x－1

x(x+1)⋯(x+n－1)

対数部分を展開する。

log

n! n^x－1

x(x+1)⋯(x+n－1)

= (x－1)log n +

n
∑
k = 1

( log k － log (k＋x－1) )

f(t) ≡ log t － log (t＋x－1)にEuler-Maclaurinの公式を適用する。

n
∑
k = 1

f(k)

∫

n

1

( log t － log (t＋x－1) )dt

( －log x + log n － log (n＋x－1) )

4
∑
k = 1

B_k+1

(k+1)!

( f^(k)(n) － f^(k)(1) )

－

(－1)⁵

∫

n

1

B₅(t－[t])f⁽⁵⁾(t)dt

右辺１行目は次のようになる。

t log t － (t＋x－1) log(t＋x－1)

= n log n + (n＋x－1) log(n＋x－1) + x log x

３以上の奇数nではB_n = 0であるから、右辺３行目は

B₂

－

t＋xー1

B₄

t³

－

(t＋xー1)³

12x

－

360x³

+ C₃ + O

+ O

n³

と書ける。C₃は定数項をまとめたものである。右辺４行目は、B₅(t－[t])が積分区間で有界であることから

∫

n

1

B₅(t－[t])

t⁵

= C₄ + O

n⁴

と書ける。ここまでの結果をまとめる。

log

n! n^x－1

x(x+1)⋯(x+n－1)

(x－1)logn+nlogn+(n＋x－1)log(n＋x－1)+xlogx+

(－logx+logn－log(n＋x－1))

12x

－

360x³

+ C₃ + C₄ + O

+ O

n³

+ O

n⁴

－ log

1 ＋

x－1

ⁿ

1 ＋

x－1

^x－1/2 +

x －

log x

12x

－

360x³

+ C₃ + C₄ + O

+ O

n³

+ O

n⁴

ここでn → ∞とし、定数項をC ≡ 1 + C₃ + C₄とまとめると

log Γ(x)

－ x +

x －

log x +

12x

－

360x³

+ C

となり、a ≡ e^Cとおいて

Γ(x) ∼ ax^x－1/2e^－x, (x → ∞)

が成り立つ。
定数aを求めるためにWallisの公式に

n! = Γ(n+1) = nΓ(n) ∼ nan^n－1/2e^－n

2n! = Γ(2n+1) = 2nΓ(2n) ∼ 2na(2n)^2n－1/2e^－2n

を代入する。

√π =

lim
n → ∞

2²ⁿn²a²n^2n－1e^－2n

2na(2n)^2n－1/2e^－2n√n

√2

したがって、a = √2πである。■

系2.2.4.4 階乗形

n! ∼ √2πnnⁿe^－n, (n → ∞), n ∈ ℕ

証明

n! = Γ(n+1) = nΓ(n)■

Starlingの公式における誤差評価については次が成り立つ。

定理2.2.4.7 誤差評価

Γ(x) = √2πx^x－1/2e^－xe^μ(x), x ＞ 0

但し、

μ(x) =

12x

, 0 ＜ θ ＜ 1

証明

演習とする。■

系2.2.4.9

√2πnnⁿe^－n ＜ n! ＜ √2πnnⁿe^－ne^1/12n, n ∈ ℕ

2.2.5 参考文献

[1] 高木貞治, 解析概論改訂第3版, 岩波書店, 2010

[2] 杉浦光夫, 解析入門Ⅰ, 東京大学出版会, 1980

[3] グレアム, クヌース, パタシェニク, コンピュータの数学, 共立出版, 1993

註　　釈

*1	領域内の各点の近傍で一様収束すること。

数　　学

部分積ぶぶんせき, partial product
無限乗積むげんじょうせき, infinite product
広義一様収束こうぎいちようしゅうそく, uniform convergence in the wider sense
ζ関数ぜーたかんすう, ζ function
Γ関数がんまかんすう, Γ function
Β関数べーたかんすう, Β function
Gaussの公式がうすのこうしき, Gauss's formula
Weierstrassの公式わいえるしゅとらすのこうしき, Weierstrass's formula
Eulerの定数おいらーのていすう, Euler's constant
二重階乗にじゅうかいじょう, double factorial
Wallisの公式うぉりすのこうしき, Wallis's formula
Starlingの公式すたーりんぐのこうしき, Starling's formula