5.4節 Γ分布
著者:梅谷 武
語句:Γ分布
Γ分布について述べる。
作成:2012-02-18
更新:2012-02-26
5.4 Γ分布
5.4.1 分布
 a, b ＞ 0を定数とするとき、(ℝ,B1)上の次の密度関数fが定める分布をΓ分布がんまぶんぷ, Γ distributionといい、Γ(a,b)で表わす。

密度関数

f(x) ≡ lc96
1
baΓ(a)
xa－1e－x/b,
x
＞
0
0,
x
≦
0
 これが確率測度を定めること、すなわち
∫∞
 
0
f(x)dx
 =
1
baΓ(a)
∫∞
 
0
xa－1e－x/bdx
 = 1
が成り立つことは、x/b = yとおくと
∫∞
 
0
xa－1e－x/bdx
 =
∫∞
 
0
(by)a－1e－ybdy
 = ba
∫∞
 
0
ya－1e－ydy
 = ba Γ(a)
となることからわかる。
5.4.2 平均と分散
 x/b = yとおくと
∫∞
 
0
xae－x/bdx
=
∫∞
 
0
(by)ae－ybdy
 = ba+1
∫∞
 
0
y(a+1)－1e－ydy
=
ba+1Γ(a+1) = ba+1aΓ(a)
より

平均

m =
1
baΓ(a)
∫∞
 
0
xae－x/bdx
 = ba
 x/b = yとおくと
∫∞
 
0
xa+1e－x/bdx
=
∫∞
 
0
(by)ae－ybdy
 = ba+2
∫∞
 
0
y(a+2)－1e－ydy
=
ba+2Γ(a+2) = ba+2a(a+1)Γ(a)
より
1
baΓ(a)
∫∞
 
0
xa+1e－x/bdx
 = b2a(a+1)
したがって

分散

σ2 = b2a(a+1) － b2a2 = b2a
5.4.3 グラフ

graph007.r

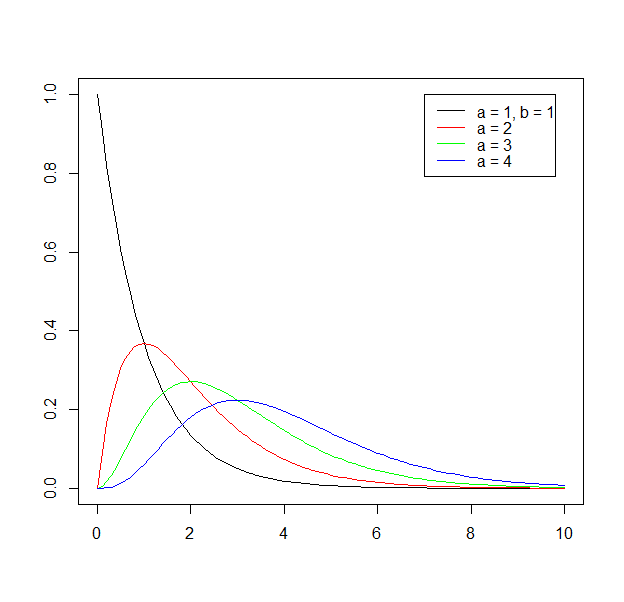
 Γ(a,b), a = 1, 2, 3, 4, b = 1を描く。
x <- seq( 0, 10, 0.1 )
plot( x, dgamma( x, 1, scale=1, log=FALSE ),
  type="l", xlab="", ylab="" )
points( x, dgamma( x, 2, scale=1, log=FALSE ), type="l", col="red" )
points( x, dgamma( x, 3, scale=1, log=FALSE ), type="l", col="green" )
points( x, dgamma( x, 4, scale=1, log=FALSE ), type="l", col="blue" )
legend( 7, 1,
  legend = c( "a = 1, b = 1", "a = 2", "a = 3", "a = 4" ),
  col = c("black","red","green","blue"),
  lty = 1 )
図5.4.3.4 Γ分布
Γ分布
数　　学
Γ分布 がんまぶんぷ, Γ distribution