6.1節 Poisson過程
著者:梅谷 武
語句:放射性崩壊,崩壊定数,半減期,平均寿命,確率過程,計数過程,Poisson過程
確率過程は時間パラメータ付き確率変数族と定義し、放射性崩壊が単位時間当たりの崩壊確率で特徴付けられることから待ち時間分布が指数分布となることを導き、それから構成した計数過程がPoisson過程となることを示す。
作成:2012-02-08
更新:2012-02-26
確率過程とは時間によりパラメータ付けされた確率変数族{Xt}のことである。離散時間の場合はこれまで準備した確率論の枠組みで議論できる。しかし、連続時間の場合、例えば確率微分方程式について論じようとすると、関数空間に位相を入れ、そのBorel集合族により可測空間を構成し、その空間に値をもつ可測関数を考える必要が出てくる。当面そこまでは必要無いので、ここでは素朴な定義により確率過程を導入する。
これからPoisson過程の概念を段階を追いながら構築していくが、放射線計測への応用を意識し、天下り式の定義ではなく、放射性崩壊がPoisson過程であることを解説しながら進めていく。しかし、論理的な厳密さは失わないようにしている。
原子核の放射性崩壊を特徴付ける物理法則は次のように表現することができる。物理法則は数学の範囲では証明ができないので公理と考えることにする。
崩壊定数が
λ > 0であるような原子核が初期状態
t = 0で
n0個あり、時刻
t ≧ 0における個数が
n(t)であるとすると、その変化について次が成り立つ。
証明
Δtを微小時間とすると
| n(t+Δt) - n(t) = -λΔt n(t)
|
が成り立つから、個数の変化は常微分方程式の初期値問題
で表現することができる。これは次のように解ける。
■
崩壊定数が
λ > 0であるような原子核の半減期
Tは
Poisson過程を構築する準備として、まず放射性崩壊が起こるまでの待ち時間の確率分布を求める。
Δtを微小時間とすると、時間区間
[(k-1)Δt,kΔt], k=1,2,⋯で崩壊するかどうかは、成功確率
p = λΔtのBernoulli試行列と考えられる。そこで
幾何分布の確率空間を考える。
標本空間
| Ω ≡ | | =
{
ω = (ω1, ⋯, ωn, ⋯)
∣
ωn ∈ ΩB = { 0, 1 }, n ∈ ℕ
}
|
事象族
 ≡ ≡ | ∞
∏
k = 1 |  B B |
|
|
|
(Ω, ,P)
,P)上の確率変数
TΔtとして崩壊までの待ち時間を考える。各根元事象
ω| ω = (0, ⋯, 0, 1, ωn+1, ⋯),
ω1 = ⋯ = ωn-1 = 0, ωn = 1, n ≧ 1
|
について最初に崩壊する項番号
nを
n(ω)と書いたときに
μΔtはΔt → 0のとき指数分布に弱収束する。
a = kΔt, b = (k+m)Δt, k,m ∈ ℕとすると次が成り立つ。
証明
ここで、
Δt → 0とすれば
k,m → ∞となるから右辺は
となる。■
ここまでの結果をまとめる。
崩壊定数が
λ > 0であるような原子核が崩壊するまでの待ち時間
Tλは密度関数
| fλ(t) ≡ | 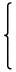 | | |
|
が定める分布
μλに従う。
崩壊定数が
λ > 0であるような原子核が崩壊する過程を初期状態
t = 0から最初に崩壊するまでの時間を確率変数
T1、
k番目に崩壊したとき
前回の崩壊からの経過時間を確率変数
Tkとするために、
( [0,∞),  [0,∞), μλ ) [0,∞), μλ )
|
の無限直積
 Ω ≡
Ω ≡ | | ,
 ≡ ≡ | ∞
∏
k = 1 |  [0,∞) [0,∞) |
|
| ,
P ≡ | |

|
を考える。確率変数列
{Tn}n ∈ ℕは独立で各
Tkは同一指数分布
μλに従っている。
Tを指数分布
μλに従う確率変数とすれば次が成り立つ。
| P( T ≦ t ) = 1 - e-λt, P( T > t ) = e-λt, t ∈ [0,∞)
|
証明
演習とする。■
とすると
{Sn}n ∈ ℕ∪{0}は
n回崩壊したときの時刻を表わす確率変数列となる。
n ≧ 1のとき
Snは
Γ分布
Γ(n,1/λ)に従う。
| P( a ≦ Sn ≦ b ) =
| | ,
[a,b] ⊂ [0,∞), n ≧ 1
|
証明
T = (T1,T2,⋯,Tn)を結合分布とすると独立性より
| | | μT1+T2+⋯+Tn([a,b]) =
P( (T1+T2+⋯+Tn)-1([a,b]) )
|
|
| | | ⋯ | | ∫ |
ℝ
| | 1[a,b](x1+x2+⋯+xn)μT(dx1dx2⋯dxn)
|
|
|
|
|
| | | ⋯ | | ∫ |
ℝ
| | 1[a,b](x1+x2+⋯+xn)μT1(dx1)μT2(dx2)⋯μTn(dxn)
|
|
|
|
| | | ⋯ | | ∫ |
ℝ
| | 1[a,b](x1+x2+⋯+xn)λne-λ(x1+x2+⋯+xn)dx1dx2⋯dxn
|
|
|
|
これは領域
| x1 ≧ 0, ⋯, xn ≧ 0, a ≦ x1 + x2 + ⋯ + xn ≦ b
|
上の積分と考えることができるから、
s = x1 + x2 + ⋯ + xnと変数変換すると
■
ここで
とおくと、
N(t)は時刻
tまでの崩壊数を表わす確率変数であり、
{N(t)}t ∈ [0,∞)は計数過程となる。各
N(t)はPoisson分布に従うのであるが、これは一般に待ち時間が同一指数分布に従う独立事象列の時刻
tまでの発生数について成り立つ。
待ち時間が同一指数分布
μλ, λ > 0に従う独立事象列
{Tn}n ∈ ℕが与えられたとき、上のように定義された時刻
tまでの発生数
N(t)はPoisson分布
P(λt)に従う。すなわち次が成り立つ。
| P( N(t) = n ) = e-λt | | , n = 0, 1, 2, ⋯
|
証明
| | |
| | |
| | | P( Sn ≦ t )P( t-s < Tn+1 ), s ≦ t |
|
| | |
| | |
■
Poisson過程
{N(t)}t ∈ [0,∞)には次の性質がある。
| (ⅰ)
| 任意の0 ≦ t1 < t2 < ⋯ < tkに対して、{N(tk)-N(tk-1)}1≦k≦nは独立。
|
| (ⅱ)
| 任意の0 ≦ s < tに対して、N(t)-N(s)はPoisson分布P(λ(t-s))に従う。
|
証明
演習とする。■
自 然
放射性崩壊 ほうしゃせいほうかい, radioactive decay
崩壊定数 ほうかいけいすう, decay constant
半減期 はんげんき, half life
平均寿命 へいきんじゅみょう, mean life
数 学
確率過程 かくりつかてい, stochastic process
計数過程 けいすうかてい, counting process
Poisson過程 ぽあそんかてい, Poisson process
 ,P)上の確率変数TΔtとして崩壊までの待ち時間を考える。各根元事象ω
,P)上の確率変数TΔtとして崩壊までの待ち時間を考える。各根元事象ω