1.5節 関数概念の拡張
著者:梅谷 武
語句:線形位相空間,Fréchet空間,台,畳み込み,単位の近似,総和核,軟化子,Radon測度,超関数,急減少関数,緩増加超関数
Fourier解析の道具であるLebesgue可測関数の畳み込み、単位の近似、総和核を準備し、線形汎関数の意味でRadon測度が関数概念の拡張になっていることを示す。さらにこれを一般化することによりSchwartzの超関数が得られることを学ぶ。超関数にも収束性や微分を定義することができて微分方程式論で重要な役割を果たす。
作成:2012-01-03
更新:2012-02-11
以後、特に断らないときは複素数体ℂ上の線形空間を考える。
線形空間
V上の半ノルム族
{pn}n∈ℕが次の条件を満たしているとする。
| (ⅰ)
| pn(f) ≦ pn+1(f), f ∈ V |
| (ⅱ)
| pn(f) = 0, n ∈ ℕ ⇒ f = 0 |
このとき、
は
V上の距離であり、これにより
Vは線形位相空間となる。
証明
演習とする。■
線形空間
V上に半ノルム族
{pn}n∈ℕによる距離を入れたとき、線形写像
T:V→ℂが連続であるための必要十分条件は、
| ∃ n ∈ ℕ, ∃ M ＞ 0 : | | ≦ Mpn(f), f ∈ V
|
証明
演習とする。■
無限遠で0に収束する連続関数全体を
| C0(ℝd) ≡ { f ∈ C(ℝd) |
| | = 0 }
|
とおく。
C0(ℝd)はノルム
と関数の積により可換Banach環となる。
証明
演習とする。■
一般に位相空間
X上の複素数値関数
fについて、その
台だい, supportを
| supp f = { x ∈ X | f(x) ≠ 0 }
|
によって定義する。
ℝd上の連続関数全体の集合を
C(ℝd)で表わす。コンパクト台をもつ連続関数全体を
| Cc(ℝd) ≡ { f ∈ C(ℝd) | supp f : コンパクト }
|
とおく。
| f ∈ Lp(ℝd), 1≦p≦∞, g ∈ L1(ℝd)
⇒ f * g ∈ Lp(ℝd)
|
さらに次が成り立つ。
証明
演習とする。■
畳み込みには関数を滑らかにする効果がある。
| (ⅰ)
| | f ∈ Lp(ℝd), 1≦p≦∞,
g ∈ Cc(ℝd)
⇒ f * g ∈ C(ℝd)
|
|
| (ⅱ)
| | f ∈ Lp(ℝd), 1≦p≦∞,
g ∈ Cc∞(ℝd)
⇒ f * g ∈ C∞(ℝd)
|
|
証明
演習とする。■
L1(ℝd)は畳み込みを積とする単位元をもたない可換Banach環となる。
証明
演習とする。■
K ∈ L1(ℝd), ∫ℝdK(x)dx = 1のとき、
は総和核である。
証明
演習とする。■
Kt ∈ L1(ℝd), t ＞ 0が総和核のとき次が成り立つ。
| (ⅰ)
| | f ∈ Lp(ℝd), 1≦p＜∞
⇒ | | p → 0 (t → 0)
|
|
| (ⅱ)
| | f ∈ C0(ℝd)
⇒ | | ∞ → 0 (t → 0)
|
|
証明
演習とする。■
証明
演習とする。■
| (ⅰ)
| Cc(ℝd)はLp(ℝd), 1≦p＜∞で稠密である。
|
| (ⅱ)
| Cc(ℝd)はC0(ℝd)で稠密である。
|
証明
演習とする。■
Radon測度については一般に局所コンパクトHausdorff空間上で議論できるが、ここでは簡単のためにℝdに制限する。
ℝd上の有限なBorel測度
μについて次が成り立つ。
| (ⅰ)
| K ∈ ℝd：compact ⇒ μ(K) ＜ ∞ |
| (ⅱ)
| ∀ε＞0, ∀A∈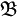 (ℝd)：
∃ F：closed, ∃ U:open, F⊂A⊂U, μ(U － F) ＜ ε |
証明
演習とする。■
複素数値Radon測度とは実部と虚部がそれぞれRadon測度であるものをいう。
Cc(ℝd)を
∞ノルム空間と考えるとき、その上の線形汎関数
Tは複素数値Radon測度
μにより、次のように一意的に表現される。
証明
演習とする。■
Rieszの定理により、ℝd上の関数のある種の拡張であるRadon測度がCc(ℝd)上の線形汎関数と同一視できることがわかった。Schwartzの超関数はこの考えをさらに進めてCc∞(ℝd)上の線形汎関数を関数の拡張と考えるものである。
コンパクト台をもつ
C∞級関数全体を
 (ℝd) ≡ { f ∈ Cc(ℝd) | f : C∞級 }
|
とおく。
(ℝd)は
Lp(ℝd), 1≦p＜∞で稠密である。
証明
演習とする。■
ℝd上の
C∞級関数
fに対する微分作用素を次のように書く。
| α = (α1, ⋯, αd), | | = α1 + ⋯ + αd,
αi ∈ ℕ ∪ {0}
|
K ⊂ ℝdをコンパクト部分集合とするとき、台が
Kに含まれる
C∞級関数全体を
K(ℝd)とおく。このとき、半ノルム族
は
命題1.5.1.3の条件を満たす。
K ⊂ ℝdをコンパクト部分集合とするとき、
K(ℝd)は上の半ノルム族によりFréchet空間となる。
証明
演習とする。■
ℝd上の可測かつ局所可積分すなわち任意のコンパクト集合上で可積分な関数
fは、次の意味で超関数となる。
| 〈 f, φ 〉 = | | ,
φ ∈ (ℝd)
|
ℝd上のRadon測度
μは次の意味で超関数となる。
| 〈 μ, φ 〉 = | | ,
φ ∈ (ℝd)
|
| 〈 δ, φ 〉 = φ(0),
φ ∈ (ℝd)
|
| 〈 Y, φ 〉 = | | ,
φ ∈ (ℝ)
|
'(ℝd)は
ℂ上の線形空間である。
証明
演習とする。■
T ∈ '(ℝd), f ∈ C∞(ℝd)のとき、
| 〈 fT, φ 〉 ≡ 〈 T, fφ 〉,
φ ∈ (ℝ)
|
は超関数となる。
証明
演習とする。■
T ∈ '(ℝd)のとき、
| 〈 | | , φ 〉 ≡
－ 〈 T, | | 〉,
φ ∈ (ℝ)
|
は超関数となる。
証明
演習とする。■
T ∈ '(ℝd)のとき、
| 〈 DαT, φ 〉 ≡
(－1)α 〈 T, Dαφ 〉,
φ ∈ (ℝ)
|
は超関数となる。
証明
演習とする。■
| 〈 Y', φ 〉 = － | |
= φ(0) = 〈 δ, φ 〉
|
超関数列
{Tn}n∈ℕが超関数
Tに収束するとは、任意の
φ∈(ℝd)について次が成り立つことをいう。
(ℝd)の位相についてはここでは触れないが、
(ℝd)は線形位相空間となり、
'(ℝd)の強位相による収束と上の定義は一致する。
超関数列
{Tn}n∈ℕにおいて、任意の
φ∈(ℝd)について
{〈 Tn, φ 〉}n∈ℕが有限確定値をもつとき、
となる超関数
Tが一意的に存在する。
証明
Banach-Steinhausの定理の特別な場合と考える。■
超関数列
{Tn}n∈ℕにおいて、
が収束すれば、その極限
は超関数である。
証明
演習とする。■
超関数級数
S = ∑nTnが収束すれば、任意の
αについて次が成り立つ。
証明
演習とする。■
Schwartzの超関数の中でも、Fourier変換や定数係数偏微分方程式を扱うときに都合のよい性質をもつクラスが緩増加超関数である。緩増加超関数は急減少関数空間上の線形汎関数として定義される。
急減少関数
f ∈ S(ℝd)に対して
と定義する。
{pn}n∈ℕは半ノルム族であり、
命題1.5.1.3の条件を満たす。これにより
S(ℝd)は線形位相空間となる。
証明
演習とする。■
(ℝd)は
S(ℝd)において稠密である。
証明
演習とする。(証明には次節の軟化子を使う)■
緩増加超関数の定義域を
(ℝd)に制限すると超関数になっており、
S'(ℝd) ⊂ '(ℝd)と考えることができる。
一般に
'(ℝd)の元としての超関数
Tが緩増加であるとは、
| ∃ k ∈ ℕ, ∃ C ＞ 0：
| | ≦ C pk(φ),
φ ∈ (ℝd)
|
が成り立つことであるが、このような超関数
Tは定義域を
S(ℝd)に拡張することができる。逆に任意の
S'(ℝd)の元は緩増加であるから、超関数の緩増加の概念は上の定義と矛盾しない。
S'(ℝd)は
'(ℝd)の部分線形空間であり、微分作用素に関して閉じている。
証明
演習とする。■
T ∈ S'(ℝd), f ∈ S(ℝd)のとき、
| 〈 fT, φ 〉 ≡ 〈 T, fφ 〉,
φ ∈ S(ℝ)
|
は緩増加超関数となる。
証明
演習とする。■
T ∈ S'(ℝd), P(x) ∈ ℂ[x]のとき、
| 〈 P(x)T, φ 〉 ≡ 〈 T, P(x)φ 〉,
φ ∈ S(ℝ)
|
は緩増加超関数となる。
証明
演習とする。■
緩増加超関数列
{Tn}n∈ℕにおいて、任意の
φ∈S(ℝd)について
{〈 Tn, φ 〉}n∈ℕが有限確定値をもつとき、
となる緩増加超関数
Tが一意的に存在する。
証明
演習とする。■
数 学
線形位相空間 せんけいいそうくうかん, topological linear space
Fréchet空間 ふれしぇくうかん, Fréchet space
台 だい, support
畳み込み たたみこみ, convolution
単位の近似 たんいのきんじ, approximation of unit
総和核 そうわかく, summation kernel
軟化子 なんかし, mollifier
Radon測度 らどんそくど, Radon measure
超関数 ちょうかんすう, distribution
急減少関数 きゅうげんしょうかんすう,
rapidly decreasing function
緩増加超関数 かんぞうかちょうかんすう,
slowly increasing distribution
