1.2節 可測関数と積分
著者:梅谷 武
語句:可測写像,可測関数,定義関数,特性関数,単関数,可積分,ほとんど至る所,σ-有限,直積測度空間
一般の集合上の可測空間における可測関数とその積分について述べる。測度さえあれば、位相構造が無くても積分が定義できることを学ぶ。
作成:2011-12-09
更新:2012-02-11
可測空間
(Ω,
)上の
ℝ値関数
fが
-可測であるための必要十分条件は、任意の
a ∈ ℝに対して、
f－1([－∞,a]), f－1([－∞,a)),
f－1([a,∞]), f－1((a,∞]))のいずれかが
に含まれることである。
証明
演習とする。■
可測空間
(Ω,)上の
ℝ値
-可測関数
g1,⋯,gdと
(ℝd,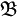
d)上の
ℝ値
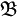d-可測関数
fに対して、その合成関数
は
-可測である。
証明
演習とする。■
可測空間
(Ω,)上の
ℝ値
-可測関数
f,gに対して、
| af+bg, fg, |f|, max(f,g), min(f,g), a,b ∈ ℝ
|
は
-可測である。
証明
演習とする。■
可測空間
(Ω,)上の
ℝ値
-可測関数
fに対して、
| f＋(ω) ≡ max( f(ω), 0 ), f－(ω) ≡ max(－f(ω), 0 ), ω ∈ Ω
|
は
-可測である。
証明
演習とする。■
可測空間
(Ω,)上の
ℝ値
-可測関数列
{ fn }n ∈ ℕに対して、
は
-可測である。
証明
演習とする。■
可測空間
(Ω,)上の実数値関数
fが
単関数たんかんすう, simple functionであるとは、
Ωの有限分割
| Ω = | | , Ak ∈ ,
Ak ∩ Al = ∅, k,l = 1,⋯,n
|
と定数
a1, ⋯, an ∈ ℝにより、次のように表現できることである。
単関数の表現は一意ではない。
可測空間
(Ω,)上の単関数は
-可測である。
証明
演習とする。■
可測空間
(Ω,)上の非負
ℝ値関数
fが
-可測であるための必要十分条件は、単調増加非負単関数列
{φn}n∈ℕ, 0≦φ1≦⋯≦φn≦⋯が存在して、
となることである。但し、極限は
∞となる場合を含む。
証明
演習とする。■
非負可測関数に収束する単関数列を近似単関数列と呼ぶことにする。一般の可測関数
fは非負
ℝ値関数の差
と分解できるため、上の定理は次のように拡張することができる。
可測空間
(Ω,)上の
ℝ値関数
fが
-可測であるための必要十分条件は、近似単関数列
{φn}n∈ℕが存在して、
となることである。但し、極限は
±∞となる場合を含む。
証明
演習とする。■
測度空間
(Ω,,μ)上の非負単関数
に対して、その可測集合
A ∈ 上の積分を次のように定義する。
上の積分の定義は単関数の表現によらず一意的に定まる。
証明
演習とする。■
測度空間
(Ω,,μ)上の非負単関数
φ, ψについて、次が成り立つ。
a, b ≧ 0, A,B ∈ , A ∩ B = ∅とする。
証明
演習とする。■
測度空間
(Ω,,μ)上の単調増加非負単関数列
{φn}, {ψn}が同じ極限を持つ、すなわち、
ならば
証明
演習とする。■
この補題により、非負可測関数の積分を定義することができる。
測度空間
(Ω,,μ)上の非負
ℝ値
-可測関数
fに対して、それを近似する単調増加非負単関数列
{φn}により、その可測集合
A ∈ 上の積分を次のように定義する。
測度空間
(Ω,,μ)上の
ℝ値
-可測関数
fが
Ω上
可積分かせきぶん, integrableであるとは、
となることである。このとき、
f = f＋ － f－と非負可測関数の差に分解すると、それぞれ可積分で積分は有限値となる。そこで可積分関数
fの可測集合
A ∈ 上の積分を次のように定義する。
測度空間
(Ω,,μ)上の可積分関数
f,gについて、
af+bgも可積分で次が成り立つ。
a, b ∈ ℝ, A,B ∈ , A ∩ B = ∅とする。
証明
演習とする。■
測度空間
(Ω,,μ)上の複素数値関数
fが
-可測とは、その実部、虚部が
-可測であることをいう。
|f|が
Ω上可積分であるとき、可測集合
A ∈ 上の積分を次のように定義する。
測度空間
(Ω,,μ)上の複素数値可積分関数
fについて、次が成り立つ。
証明
演習とする。■
測度空間
(Ω,,μ)上の非負可測関数列
{fn}について、次が成り立つ。
証明
演習とする。■
測度空間
(Ω,,μ)上の単調増加非負可測関数列
{fn}について、次が成り立つ。
証明
演習とする。■
測度空間
(Ω,,μ)上の可積分関数
fと可測集合列
{An}, A = ∪n Anについて、次が成り立つ。
証明
演習とする。■
測度空間
(Ω,,μ)上の非負可測関数列
{fn}について、次が成り立つ。
証明
演習とする。■
測度空間
(Ω,,μ)上の可測関数列
{fn}が、非負可積分関数
gにより、
と値が抑えられており、かつその極限
が存在するならば、次が成り立つ。
証明
演習とする。■
積分の収束定理は、収束をほとんど至る所収束と置き換えても成り立つ。
証明
演習とする。■
測度空間
(Ω,,μ)が
σ-有限しぐまゆうげん, σ-finiteとは、次のような部分集合列
{Ak}k ∈ ℕ, Ak ∈ が存在することである。
| μ(Ak) ＜ ∞, A1 ⊂ A2 ⊂ ⋯ Ak ⊂ ⋯,
Ω = | |
|
σ-有限な測度空間
(Ω1,1,μ1),⋯,(Ωn,d,μd)が与えられたとき、σ-加法族の直積
1×⋯×d上の測度で
| μ1×⋯×μd(A1×⋯×Ad) =
μ1(A1)⋯μd(Ad), Ak ∈ k
|
となるものが一意的に存在する。
証明
演習とする。■
直積測度空間
(Ω1×⋯×Ωd,1×⋯×d,μ1×⋯×μd)において、
1×⋯×d-可測関数は、その第
k成分以外を固定したとき
k-可測である。
証明
演習とする。■
上の補題の逆は成り立たない。すなわち、各成分について可測であっても、直積測度で可測とは限らない。
非負可測関数に対するFubiniの定理をd = 2の場合に述べる。
証明
演習とする。■
σ-有限な測度空間
(Ωk,k,μk), k=1,2の直積空間
(Ω1 × Ω2,1 × 2,μ1 × μ2)上の複素
μ1×μ2-可積分関数
fについて、次が成り立つ。
| (ⅰ)
| |
| (ⅱ)
| | =
| | ∫ |
Ω2
|  | |  μ2(dω2) |
|
|
|
|
証明
演習とする。■
完備化直積測度空間
(Ω1×⋯×Ωd,1×⋯×d,μ1×⋯×μd)において、
1×⋯×d-可測関数は、その第
k成分以外を固定したとき
k-可測である。
証明
演習とする。■
σ-有限な測度空間
(Ωk,k,μk), k=1,2の完備化直積空間
(Ω1 × Ω2,1 × 2,μ1 × μ2)上の複素
μ1 × μ2-可積分関数
fについて、次が成り立つ。
| (ⅰ)
| |
| (ⅱ)
| | =
| | ∫ |
Ω2
| | | μ2(dω2) |
|
|
|
|
証明
演習とする。■
数 学
可測写像 かそくしゃぞう, mesurable mapping
可測関数 かそくかんすう, mesurable function
定義関数 ていぎかんすう, defineing function
特性関数 とくせいかんすう, characteristic function
単関数 たんかんすう, simple function
可積分 かせきぶん, integrable
ほとんど至る所 ほとんどいたるところ, almost everywhere, a.e.
σ-有限 しぐまゆうげん, σ-finite
直積測度空間 ちょくせきそくどくうかん, product measure space
)を可測空間とするとき、写像f:Ω → Xが