4.4節 幾何分布
著者:梅谷 武
語句:幾何分布
可算個のBernoulli試行列において成功するまでの試行回数により定まる幾何分布について述べる。
作成:2012-01-21
更新:2012-02-12
成功確率
pのBernoulli試行列において、試行を成功するまで繰り返すことを考える。標本空間としては可算個のBernoulli試行列の空間が必要になる。
標本空間
| Ω ≡ | | =
{
ω = (ω1, ⋯, ωn, ⋯)
∣
ωn ∈ ΩB = { 0, 1 }, n ∈ ℕ
}
|
事象族
 ≡ ≡ | ∞
∏
k = 1 |  B B |
|
|
|
(Ω, ,P)
,P)上の実確率変数
Xとして次のものを考える。各根元事象
ω| ω = (0, ⋯, 0, 1, ωn+1, ⋯),
ω1 = ⋯ = ωn-1 = 0, ωn = 1, n ≧ 1
|
について最初に成功する項番号
nを
n(ω)と書いたときに
n ≧ 1に対して、
| X-1(n) = {0} × ⋯ × {0} × {1} ×
| |
|
であるから、次が成り立つ。
| μX({n}) = P(X-1({n})) = pqn-1, n ≧ 1
|
qに関する冪級数
∑nqnは収束円
{ q < 1 }内で一様収束するから、項別微分可能であり
| 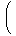 | ∞
∑
n = 0 | qn 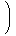 = = | | =
| |
|
|
したがって
平均
| | | ∫ |
ℝ
| x 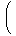
| | 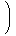 (dx) (dx) |
|
| |
|
| | |
分散は
σ2 = E[X2] - E[X]2により計算する。
| | | ∫ |
ℝ
| x2 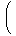
| | 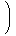 (dx) (dx) |
|
| |
|
| | |
この和を求めるため、まず
の両辺に
qをかけて微分すると
よって、次のようになる。
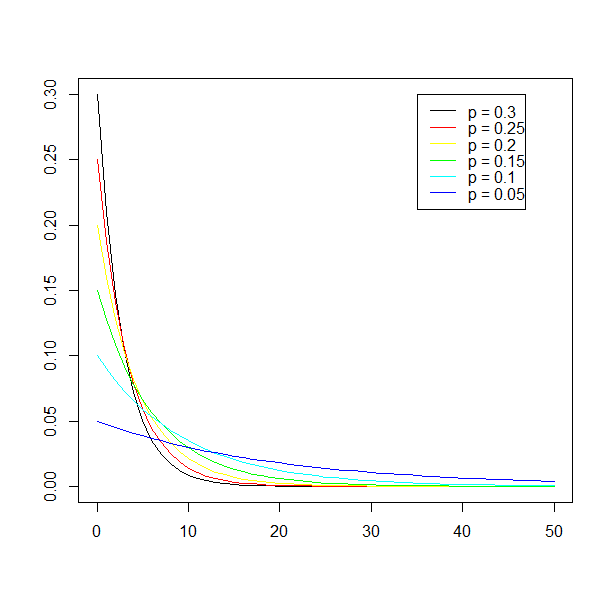
G(p), p = 0.05, 0.1, 0.15, 0.2, 0.25, 0.3を描く。
k <- 0:50
plot( k, dgeom( k, prob=0.3 ), type="l", xlab="", ylab="" )
points( k, dgeom( k, prob=0.25 ), type="l", col="red")
points( k, dgeom( k, prob=0.2 ), type="l", col="yellow")
points( k, dgeom( k, prob=0.15 ), type="l", col="green")
points( k, dgeom( k, prob=0.1 ), type="l", col="cyan")
points( k, dgeom( k, prob=0.05 ), type="l", col="blue")
legend( 35, 0.3,
legend = c( "p = 0.3", "p = 0.25", "p = 0.2", "p = 0.15",
"p = 0.1", "p = 0.05" ),
col = c("black","red","yellow","green","cyan","blue"),
lty = 1 )数 学
幾何分布 きかぶんぷ, geometric distribution
 ,P)上の実確率変数Xとして次のものを考える。各根元事象ω
,P)上の実確率変数Xとして次のものを考える。各根元事象ω