4.5節 Poisson分布
著者:梅谷 武
語句:Poisson分布
成功確率が小さく試行回数が多い場合の二項分布の近似であるPoisson分布について述べる。
作成:2012-01-26
更新:2012-03-10
4.5 Poisson分布
4.5.1 分布
 可測空間(ℝ,B1)上の次の離散分布をPoisson分布ぽあそんぶんぷ, Poisson distributionといい、P(λ)で表わす。

分布

∞
∑
k = 0
e－λ
λk
k!
δk
 これが一次元離散分布になっていることは
∞
∑
k = 0
e－λ
λk
k!
 = e－λ
∞
∑
k = 0
λk
k!
 = e－λeλ = 1
からわかる。
4.5.2 平均と分散

平均

m =
∞
∑
k = 0
ke－λ
λk
k!
 = λ
∞
∑
k = 1
e－λ
λk－1
(k－1)!
 = λ
∞
∑
k = 0
e－λ
λk
k!
 = λ
分散はσ2 = E[x2] － E[x]2により計算する。
E[x2]
=
∞
∑
k = 0
k2e－λ
λk
k!
 = λ
∞
∑
k = 1
ke－λ
λk－1
(k－1)!
=
λ
∞
∑
k = 1
(k－1)e－λ
λk－1
(k－1)!
 + λ
∞
∑
k = 1
e－λ
λk－1
(k－1)!
=
λ2 + λ
よって、次のようになる。

分散

σ2 = λ2 + λ － λ2 = λ
4.5.3 再生性

定理4.5.3.1 Poisson分布の再生性

 独立な確率変数X, YがそれぞれPoisson分布P(λ1), P(λ2)に従っているとき、それらの和Z ≡ X + YはPoisson分布P(λ1+λ2)に従う。

証明

P(Z = k)
=
k
∑
j = 0
P(X = j)P(Y = k－j)
=
k
∑
j = 0
λ1j
j!
e－λ1
λ2k－j
(k－j)!
e－λ2
=
e－(λ1＋λ2)
k!
k
∑
j = 0
k!
j!(k－j)!
λ1jλ2k－j
=
e－(λ1＋λ2)
(λ1＋λ2)k
k!
■
4.5.4 二項分布のPoisson近似
 二項分布列Bin(n,p(n)), 0 ＜ p(n) ＜ 1
n∙p(n) longrightarrow λ, p(n) longrightarrow 0 (n → ∞)
の極限はPoisson分布P(λ)になっている。
 Bin(n,p(n))の分布は
μn =
n
∑
k = 0
(n
k		)
p(n)kq(n)n－kδk
であるから、次の命題によりBin(n,p(n))がP(λ)に弱収束することがわかる。

定理4.5.4.3 Poisson

 0 ＜ p(n) ＜ 1, q(n) ≡ 1 － p(n), n ∈ ℕ
n∙p(n) longrightarrow λ, p(n) longrightarrow 0 (n → ∞)
ならば、任意のk ∈ ℕ ∪ {0}に対して次が成り立つ。
 
lim
n → ∞
(n
k		)
p(n)kq(n)n－k
 = e－λ
λk
k!

証明

Pn(k) ≡
(n
k		)
p(n)kq(n)n－k, k = 0, 1, ⋯, n
とおくと
Pn(k)
Pn(0)
 =
k－1
∏
m = 0
Pn(m＋1)
Pn(m)
ここで、詳細は省略するが
 
lim
n → ∞
Pn(m＋1)
Pn(m)
 =
λ
m + 1
より
 
lim
n → ∞
Pn(k)
Pn(0)
 =
k－1
∏
m = 0
λ
m + 1
 =
λk
k!
であり、さらに
 
lim
n → ∞
Pn(0)
 =
 
lim
n → ∞
lb48 1 －
λ
n
rb48
 = e－λ
より
 
lim
n → ∞
Pn(k)
 = e－λ
λk
k!
■
4.5.5 Poisson分布の正規近似
 Xi, i = 1,2,⋯をPoisson分布P(λ)に従う独立な確率変数列とすると
Sn = X1 + X2 + ⋯ + Xn,  n = 1,2,⋯
はPoisson分布の再生性によりP(nλ)に従う。中心極限定理から
Sn － nλ
√nλ
は標準正規分布N(0,1)に法則収束する。このことから、nが大きければP(nλ)は正規分布N(nλ,nλ)で近似できることがわかる。nλをλに置き換えることにより次の命題が得られる。

命題4.5.5.2

 λが大きいときPoisson分布P(λ)は正規分布N(λ,λ)で近似できる。
4.5.6 グラフ

graph003.r

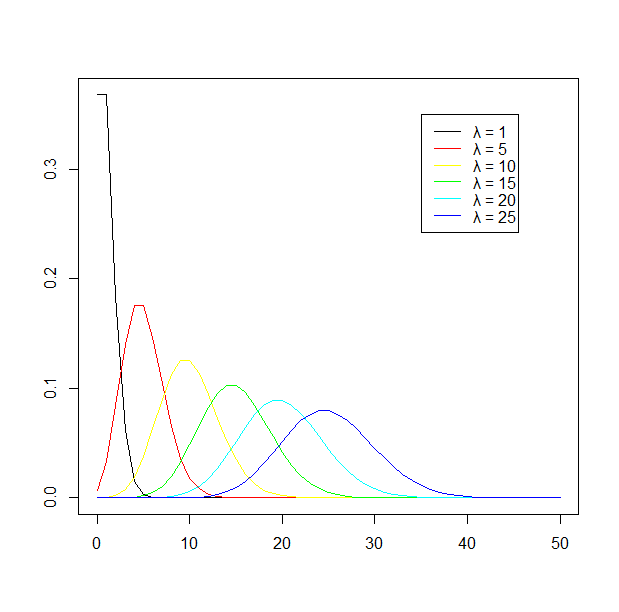
 P(λ), λ = 1, 5, 10, 15, 20, 25を描く。
k <- 0:50
plot( k, dpois( k, lambda=1 ), type="l", xlab="", ylab="" )
points( k, dpois( k, lambda= 5 ), type="l", col="red")
points( k, dpois( k, lambda=10 ), type="l", col="yellow")
points( k, dpois( k, lambda=15 ), type="l", col="green")
points( k, dpois( k, lambda=20 ), type="l", col="cyan")
points( k, dpois( k, lambda=25 ), type="l", col="blue")
legend( 35, 0.35,
  legend = c( "λ = 1", "λ = 5", "λ = 10", "λ = 15",
    "λ = 20", "λ = 25" ),
  col = c("black","red","yellow","green","cyan","blue"),
  lty = 1 )
図4.5.6.4 Poisson分布
Poisson分布

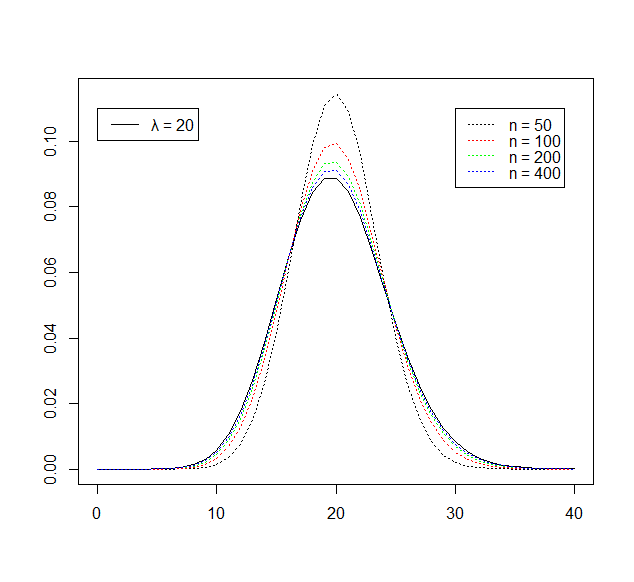
graph004.r

 P(20)とBin(50,0.4),Bin(100,0.2),Bin(200,0.1),Bin(400,0.05)を比較する。
k <- 0:40
plot( k, dbinom( k, 50, prob=0.4 ), type="l", xlab="", ylab="",
  lty="dotted" )
points( k, dpois( k, lambda= 20 ), type="l")
points( k, dbinom( k, 100, prob=0.2 ), type="l", col="red",
  lty="dotted" )
points( k, dbinom( k, 200, prob=0.1 ), type="l", col="green",
  lty="dotted" )
points( k, dbinom( k, 400, prob=0.05 ), type="l", col="blue",
  lty="dotted" )
legend( 30, 0.11,
  legend = c( "n = 50", "n = 100", "n = 200", "n = 400" ),
  col = c("black","red","green","blue"),
  lty = "dotted" )
legend( 0, 0.11,
  legend = c( "λ = 20" ),
  col = c("black"),
  lty = 1 )
図4.5.6.8 二項分布との比較
二項分布との比較

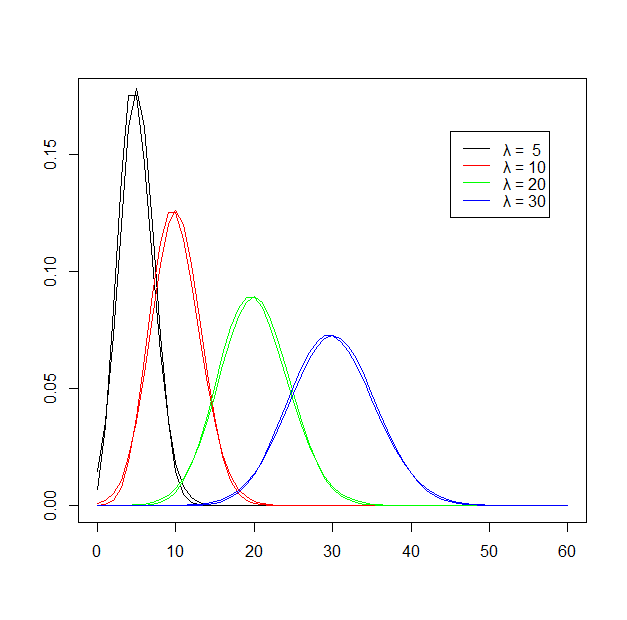
graph004b.r

 P(λ)とN(λ,λ)を比較する。λ = 5,10,20,30
k <- 0:60
plot( k, dpois( k, lambda=5 ), type="l", xlab="", ylab="" )
points( k, dnorm( k, 5, sqrt(5) ), type="l" )
points( k, dpois( k, lambda=10 ), type="l", col="red")
points( k, dnorm( k, 10, sqrt(10) ), type="l", col="red")
points( k, dpois( k, lambda=20 ), type="l", col="green")
points( k, dnorm( k, 20, sqrt(20) ), type="l", col="green")
points( k, dpois( k, lambda=30 ), type="l", col="blue")
points( k, dnorm( k, 30, sqrt(30) ), type="l", col="blue")
legend( 45, 0.16,
  legend = c( "λ =  5", "λ = 10", "λ = 20", "λ = 30" ),
  col = c("black","red","green","blue"),
  lty = 1 )
図4.5.6.12 正規分布との比較
正規分布との比較
数　　学
Poisson分布 ぽあそんぶんぷ, Poisson distribution