原始根

著者:梅谷武
語句:ウィルソン,原始根,離散指数,底,離散対数,直積分解,n冪剰余,n冪非剰余,平方剰余,平方非剰余

原始根について述べる。

作成:2006-06-16
更新:2021-03-17

オイラーは『数論研究』において、素数pを法として考える場合、

{ 1=r⁰,r,r²,⋯,r^p－1 }

がすべて異なるような数rがφ(p－1)個存在することを発見し、これを原始根と呼びました。これは既約剰余類群(ℤ/pℤ)^×が位数p－1の巡回群になっていて、その生成元がφ(p－1)個存在するということです。オイラー自身は任意の素数についてその原始根の存在を証明することができませんでしたが、ガウスは『整数論』でこれを証明し、さらに任意の奇素数の冪を法とする場合も原始根が存在すること、そして2の冪が法の場合は原始根が存在しないことを示しました。この節では、まず、この原始根がどのように役に立つかを例を使って説明し、その後で任意の素数冪を法とする既約剰余類群の構造について解説します。

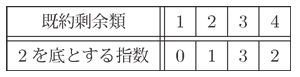
5を法として2の冪乗を計算してみます。

2⁰ ≡ 1, 2¹ ≡ 2, 2² ≡ 4, 2³ ≡ 3, 2⁴ ≡ 1

となり、既約剰余類群(ℤ/5ℤ)^×={1,2,3,4}は2で生成される巡回群になっています。これは2は法5の原始根であることを示しています。2^c≡aであるときaをbの2を底とする指数といい、これを

log₂ a = c

と書くことにします。ガウスは『整数論』で

Ind. a = c

高木貞治は『初等整数論講義』で

Ind₂ a = c

と書いていましたが、本書では暗号理論で一般的に使われている記号を採用することにします。

指数に関して一般に次の性質が成り立ちます。

a ≡ b (mod p) ⇔ log_r a ≡ log_r b (mod p－1)

また、離散対数と呼ばれるlog_r関数には対数と同じような性質があります。

log_r(ab)

log_r(a) + log_r(b)

log_r(a^k)

klog_r(a)

これらの性質から、既約剰余類の計算を指数計算に変換することができます。

例題5.6.4

3X ≡ 4 (mod 5)

この一次合同式は暗算でも簡単に解けますが、離散対数を使って解いてみます。この場合、原始根2とそれを底とする指数表が与えられていることが必要です。

表5.6.6 法5の2を底とする指数表

まず、両辺の2を底とする離散対数をとります。

log₂ 3 + log₂ X ≡ log₂ 4 (mod 4)

指数表を参照して値を代入すると

3 + log₂ X

≡

2 (mod 4)

log₂ X

≡

－1 ≡ 3 (mod 4)

となり、また指数表を参照することで解X≡3(mod 5)を得ます。

例題5.6.8

X³ ≡ 2 (mod 5)

両辺の離散対数をとると

3 log₂ X ≡ log₂ 2 ≡ 1 (mod 4)

となりますが、法4で3倍して1と合同になるものは3しかありませんから、log₂X≡3(mod 4)より、解X≡3(mod 5)を得ます。

例題5.6.10

3X² － X + 1 ≡ 0 (mod 5)

両辺に2をかけると

X² － 2X + 2

≡

0 (mod 5)

(X－1)²

≡

－1 ≡ 4 (mod 5)

ここで両辺の離散対数をとると、

2 log₂ (X－1) ≡ log₂ 4 ≡ 2 (mod 4)

法4で2倍して2と合同になるものは1と3ですから、

log₂ (X－1)

≡

1 または 3 (mod 4)

X－1

≡

2 または 3 (mod 5)

となり、解はX≡3または4(mod 5)となります。

既約剰余類群の構造

任意の法mに対して、その素因数分解をm=p₁^e₁ ⋯ p_k^e_kとすれば系5.4.66より、

(ℤ/mℤ)^× ≅ (ℤ/p₁^e₁ℤ)^× × ⋯ × (ℤ/p_k^e_kℤ)^×

と素数冪を法とする既約剰余類群の直積に分解されますから、素数冪を法とする既約剰余類群の構造がわかればすべての法の既約剰余類群の構造がわかります。

素数冪を法とする既約剰余類群の構造は次の4種類に分類されます。

(1)

法p, p:素数の場合

(ℤ/pℤ)^× ≅ ＜r＞, r^p－1 ≡ 1 (mod p)

(2)

法p^e, p:奇素数, e>1の場合

(ℤ/p^eℤ)^× ≅ ＜r＞, r^{p^e－1(p－1)} ≡ 1 (mod p^e)

(3)

法2²=4の場合

(ℤ/2²ℤ)^× ≅ ＜－1＞, (－1)² ≡ 1 (mod 4)

(4)

法2^e, e>2の場合

(ℤ/2^eℤ)^× ≅ ＜－1＞ × ＜5＞, (－1)² ≡ 5^{2^e－2} ≡ 1 (mod 2^e)

(1),(2),(3)の場合は巡回群になり、(4)の場合だけ2個の巡回群の直積になります。(1),(2)の場合、既約剰余類群の生成元を原始根げんしこん, primitive rootと呼びます。

巡回群

有理整数環ℤを加法群と考えたとき、その部分群Hは加法に関して閉じているので、任意のn∈ℤ, h∈Hに対して、

nh = h + h + ⋯ + h (n個の和)

を満たしますから、Hはℤのイデアルになっています。したがって、ℤの部分群全体の集合はイデアル全体の集合ℑ(ℤ)と一致し、定理2.4.32より、包含関係に関して(ℕ,|)と双対な束を成します。

図5.6.15 (ℕ,|)と(ℑ(ℤ),⊆)の双対性

Gが巡回群であるとしましょう。巡回群とは一個の元aで生成される群のことでした。

G = ＜a＞ = { a^k | k∈ℤ }

このとき、加法群ℤからGへの写像を

e_a:ℤ → G, k ↦ a^k

と定めると、

e_a(k+l) = a^k+l = a^k a^l = e_a(k)e_a(l)

となり、加法群から乗法群への全射準同型写像になります。巡回群Gとその生成元aによって定まるこの写像を離散指数りさんしすう, discrete exponentioalといいます。この写像の核はGの位数が無限の場合は{ 0 }、位数がnの場合は(n)=nℤですから、群の準同型定理から、

(1)	Gの位数が無限の場合、ℤ ≅ G
(2)	Gの位数がnの場合、ℤ/nℤ ≅ G

となり、すべての巡回群は加法群としてのℤかℤ/nℤと同型になることがわかります。

この同型写像の逆写像は位数が無限の場合、

log_a:G → ℤ, a^k ↦ k

位数がnの場合、

log_a:G → ℤ/nℤ, a^k ↦ k

となりますが、これをaを底てい, baseとする離散対数りさんたいすう, discrete logarithmといいます。

命題5.6.18 対数法則

巡回群G上で定義された離散対数に関して次が成り立つ。

(i)	log_a(bc) = log_a(b) + log_a(c)
(ii)	log_a(b^k) = klog_a(b)
(iii)	bが生成元のとき、log_a(b)log_b(c) = log_a(c)

証明

(i),(ii)は定義より。(iii)はlog_a(b)=k,log_b(c)=lとすればb=a^k,c=b^lであるからc=(a^k)^l= a^kl.■

巡回群がℤかℤ/nℤと同型になることから、巡回群がもつ特別な性質がいろいろとわかってきます。すぐにわかることは

(C1)	巡回群は可換である。
(C2)	巡回群の部分群は巡回群である。

ということです。

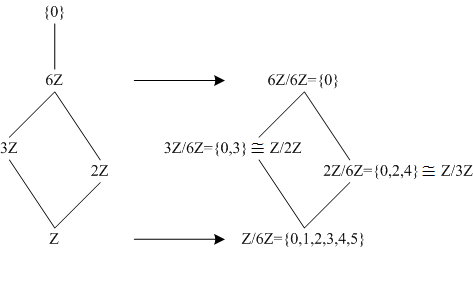
次に巡回群Gの位数nが有限の場合を考えます。ℤの部分群全体の集合は自然数の整除関係に関する束と双対になりますが、ℤ/nℤの部分群全体の集合はどのような構造を持つのでしょうか。

大雑把に言えばℤ/nℤの部分群全体の集合は、ℤの部分群全体の集合が成す束をnℤで割ってできる有限束になります。例としてn=6の場合を図示しておきます。

図5.6.23 ℤ/6ℤの部分群の成す束

一般にℤ/nℤの部分群の成す束は次のような集合です。

{ dℤ/nℤ ≅ ℤ/(n/d)ℤ | d | n }

nの約数dの集合と一対一に対応し、dに対応する部分群はℤ/(n/d)ℤと同型になります。このことを次のようにまとめておきます。

(C3)	位数nの巡回群にはnの各約数dに対してn/dを位数とする部分群が唯一つだけ存在し、それが部分群のすべてである。

巡回群G=＜a＞の位数が無限の場合は、その生成元はaとa^－1の二つしかありませんが、位数nが有限の場合は様子が違ってきます。

補題5.6.27

群Gの元aの位数がnであるとする。任意の正の整数mについてd=(m,n)とするとa^mの位数はn/dである。

証明

a^mの位数をkとし、n'=n/dとおく。a^mk=1よりn|mkであるから、n'|k.一方、n|mn'よりa^mn'=1であるからk|n'.したがってn'=k.■

この補題から次のことがわかります。

(C4)	位数nの巡回群G=＜a＞において、a^mの位数がnとなることと(m,n)=1となることは同等である。

したがって、位数nの巡回群の生成元の個数はφ(n)に等しくなります。

位数nの巡回群Gの元をその位数で分類することを考えます。Gの元の位数はnの約数ですから、O_dで位数dの元の集合を表わすとGは

G = ∪_d|n O_d

と分割されます。O_dの各元は位数dの部分群を生成しますが、それは(C3)から唯一つしか存在しませんから、O_dは位数dの部分群の生成元全体の集合に他なりません。これはφ(d)と等しくなりますから、結局

n =

∑
d|n

φ(d)

が成り立つことがわかります。これは命題5.5.36の別証明になっています。

次の補題は(ℤ/pℤ)^×における原始根の存在を証明するために使われます。

補題5.6.32

有限群Gにおいて、任意の正の整数dに対してx^d=1を満たす元が高々d個しか含まれないとき、Gは巡回群である。

証明

Gの位数をnとする。位数nの元が存在することを示せばよい。正の整数dに対して位数がdであるようなGの元の個数をψ(d)とする。ラグランジュの定理からGの元の位数はnの約数であるから、O_dで位数dの元の集合を表わすとGは

G = ∪_d|n O_d

と分割され、

n =

∑
d|n

ψ(d)

が成り立つ。aを位数dの元とすると、aが生成する部分群＜a＞={1,a,a²,⋯,a^d－1}の元はすべてx^d=1を満たすので、仮定より位数dの元はこれ以外には存在しない。したがって、

ψ(d) =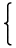

φ(d),

位数dの元が存在するとき

位数dの元が存在しないとき

となるが、一方で

n =

∑
d|n

ψ(d)

∑
d|n

φ(d)

が成り立っていることから、nの任意の約数dについてψ(d) = φ(d)であり、特にψ(n) = φ(n)＞1となり、位数nの元が存在する。■

ℤ/pℤの既約剰余類群の構造

任意の素数pについて、F_p=ℤ/pℤは標数pの有限体です。系3.6.57より、任意の正の整数dについてd次の一元代数方程式

X^d － 1 = 0

の根は高々d個ですから、補題5.6.32より既約剰余類群(ℤ/pℤ)^×は位数p－1の巡回群です。

ℤ/p^eℤの既約剰余類群の構造

まず、次の補題を準備しておきます。

補題5.6.36

pを奇素数としたときに、(k,p)=1なる整数kと、m≧1なる整数mについて、

(1+kp^m)^p = 1 + k'p^m+1, (k',p) = 1

なる整数k'が存在する。

証明

二項定理より、

(1+kp^m)^p

1 +

(

p
1

)

kp^m +

(

p
2

)

k²p^2m + ⋯ + k^pp^pm

1 + kp^m+1 +

(p－2)!2!

k²p^2m + ⋯ + k^pp^pm

1 + p^m+1 ( k +

(p－1)!

(p－2)!2!

k²p^2m + ⋯ + k^p p^{pm － m + 1} )

であるから、右辺の括弧の中をk'とおけばk≡k'(mod p)であり、(k',p)=1が成り立つ。■

奇素数pとe＞1なる整数eについて、既約剰余類群(ℤ/p^eℤ)^×は位数p^e－1(p－1)の巡回群になることを示します。

rを既約剰余類群(ℤ/pℤ)^×の原始根とすると、ある整数kによって

r^p－1 = 1 + k p

と書くことができます。まず、(k,p)=1と仮定しましょう。そうすると上の補題から、

(1+kp)^p

1 + k₁p², (k₁,p)=1

(1+kp)^p²

1 + k₂p³, (k₂,p)=1

⋯

(1+kp)^{p^e－2}

1 + k_e－2p^e－1, (k_e－2,p)=1

(1+kp)^{p^e－1}

1 + k_e－1p^e, (k_e－1,p)=1

となり、

r^{p^s(p－1)}

≢

1 (mod p^e), s＜e－1

r^{p^e－1(p－1)}

≡

1 (mod p^e)

であることから、(ℤ/p^eℤ)^×におけるrの位数はp^e－1(p－1)となり、rが(ℤ/p^eℤ)^×の原始根になっていることがわかります。

(k,p)≠1の場合は、ある整数kとt≧1によって

r^p－1 = 1 + k p^t

と書くことができます。ここでr'=r+pとおくと、

r'^p－1 = 1 + k'p, (k',p)=1

となり、(k,p)=1の場合に帰着することができます。これは二項定理より、

(r+p)^p－1

r^p－1 +

(

p－1
1

)

r^p－2p +

(

p－1
2

)

r^p－3p² + ⋯ + p^p－1

≡

1 + (p－1)r^p－2p (mod p²)

≡

1 － r^p－2p (mod p²)

となり、

(r+p)^p－1 = 1 + (kp － r^p－2)p, k∈ℤ

と書け、ここで(kp － r^p－2,p)=(r^p－2,p)=1となっています。

ℤ/2^eℤの既約剰余類群の構造

ℤ/4ℤの乗算表を次に示します。

表5.6.42 ℤ/4ℤの乗算表

この表から(ℤ/2²ℤ)^× = { 1,3 }は位数2の巡回群となることがわかります。計算の都合上、この既約剰余系として{ 1,－1 }をとることにします。

e>2のとき、既約剰余類群(ℤ/2^eℤ)^×は、奇素数pに対する既約剰余類群(ℤ/p^eℤ)^×とは異なり、巡回群にはなりません。しかし、二つの巡回群の直積として表現することができます。

一般に群の直積G=G₁ × G₂ × ⋯ × G_kは自然な埋め込み写像

G_i → G₁ × ⋯ G_i × ⋯ × G_k, a_i ↦ (1,⋯,a_i,⋯,1)

によって、その各因子G_iを正規部分群として含んでいるとみなすことができ、さらに次の条件を満たしています。

(a)	i≠jならばG_iとG_jの元は可換である。
(b)	Gの任意の元はa₁a₂⋯a_kと一意的に表わすことができる。

逆に、Gの部分群G₁,G₂,⋯,G_kが(a),(b)を満たすとすれば、写像

G₁ × G₂ × ⋯ × G_k → G, (a₁,a₂,⋯,a_k) ↦ a₁ a₂ ⋯ a_k

は群の同型写像となります。このときG₁×G₂×⋯×G_kをGの直積分解ちょくせきぶんかい, direct product decompositionといいます。

次の補題は部分群の積が直積分解になっているかどうかを判断する条件を与えています。

補題5.6.47

群Gがその部分群G₁,G₂,⋯,G_kによってG=G₁×G₂×⋯×G_kと直積分解されることと次の三つの条件が必要十分である。

(i)	G_i,i=1,⋯,kはGの正規部分群である。
(ii)	G=G₁ G₂ ⋯ G_k
(iii)	(G₁ ⋯ G_i) ∩G_i+1 = {1}, i=1,⋯,k－1

証明

[⇒](i),(ii)は条件(a),(b)から。(iii)a₁ ⋯ a_i = a_i+1とするとa₁⋯a_ia_i+1^－1=1であり、分解の一意性からa_k=1, k=1,⋯,i+1.[⇐](a) i≠jとし、任意のa_i∈G_i, a_j∈G_jについてa_ia_j=a_ja_iを示す。a_ia_ja_i^－1a_j^－1=(a_ia_ja_i^－1)a_j^－1=a_i(a_ja_i^－1a_j^－1)はG_i,G_jが正規部分群であることからG_i,G_jに含まれ、G_i∩G_j={1}に含まれる。よってa_ia_ja_i^－1a_j^－1=1よりa_ia_j=a_ja_i.(b) (ii)より任意のGの元はa₁a₂⋯a_kと分解される。a₁a₂⋯a_k=b₁b₂⋯b_kという二つの分解があったとする。i≠jなる元の可換性から、

(b₁^－1a₁) (b₂^－1a₂) ⋯ (b_k－1^－1a_k－1) = b_k a_k^－1

となり、(iii)よりb_k a_k^－1=1となり、a_k=b_kであることがわかる。同じようにしてi=1,⋯,k－1なるiについてa_i=b_iが成り立つ。■

群の直積分解に関する準備が整ったので、e＞2のときの既約剰余類群(ℤ/2^eℤ)^×の構造を調べることにしましょう。

p=2のとき補題5.6.36は成り立ちませんが、その証明からわかるようにm＞1という条件にすれば成り立ちます。

補題5.6.51

(k,2)=1なる整数kと、m＞1なる整数mについて、

(1+k2^m)² = 1 + k'2^m+1, (k',2) = 1

なる整数k'が存在する。

証明

演習とする。■

この補題をk=1,m=2に適用すると5=1+2²ですから、

5²

1 + k₁ 2³, (k₁,2)=1

5^2²

1 + k₂ 2⁴, (k₂,2)=1

⋯

5^{2^e－3}

1 + k_e－3 2^e－1, (k_e－2,2)=1

5^{2^e－2}

1 + k_e－2 2^e, (k_e－1,2)=1

となり、法2^eで考えると5の位数は2^e－2です。ϕ(2^e)=2^e－1ですから、＜5＞={ 5ⁱ | i = 0,1,⋯,2^e－2－1 }は(ℤ/2^eℤ)^×の指数2の部分群になっています。

(ℤ/2^eℤ)^× ≅ ＜－1＞ × ＜5＞

であることを示します。5≡1(mod 4)より、正の整数iについて5ⁱ≡1(mod 4)ですから、－1∉＜5＞であることがわかります。既約剰余類群は可換ですから、任意の部分群は正規部分群になり、特に＜－1＞と＜5＞は正規部分群で、＜－1＞∩＜5＞={1}が成り立っていますから、両辺の位数が等しいことから同型であることがわかります。

冪剰余

pを素数とするとき、正の整数に対して

Xⁿ ≡ a (mod p)

が解をもつとき、aはpのn冪剰余nべきじょうよ, residue of n-th powerであるといい、解をもたないとき、n冪非剰余nべきひじょうよ, non-residue of n-th powerであるといいます。

素数を法とする原始根の存在が保証されたことによって、冪剰余の判定条件に関する次の定理を容易に証明することができます。

定理5.6.56

pを素数とするとき、正の整数に対して

Xⁿ ≡ a (mod p)

が解をもつ必要十分条件は、d=(n,p－1)としたとき

a^(p－1)/d ≡ 1 (mod p)

となることである。このとき解の個数はd個である。

証明

pを法とする原始根をrとすると、Xⁿ≡a(mod p)は

n log_r X ≡ log_r a (mod p－1)

と同等であり、命題5.2.3より、d|log_raのとき、p－1を法としてd個の解をもつことがわかっている。[⇒]d|log_raであるとする。log_ra=m, m=m'dとおくと、

a^(p－1)/d ≡ r^m(p－1)/d ≡ r^m'(p－1) ≡ 1 (mod p)

となり、aは解である。[⇐]

a^(p－1)/d ≡ r^m(p－1)/d ≡ 1 (mod p)

より、p－1|m(p－1)/dであるから、d|mが成り立つことがわかる。■

系5.6.58

素数pを法とするn冪剰余は、d=(n,p－1)としたときp－1個ある既約剰余類の中にp－1/d個存在する。

法13においていくつかの例を見てみます。

表5.6.60 法13の2を底とする指数表

例題5.6.61

X³ ≡ a (mod 13)

両辺の離散対数をとると、

3 log₂ X ≡ log₂ a (mod 12)

(3,12)=3より、3冪剰余となるaに対応する指数log₂aは0,3,6,9の4個で、それに対応する既約剰余類、すなわち3冪剰余は1,5,8,12の4個です。

特にn=2,p≠2のとき、pを法とする2冪剰余を平方剰余へいほうじょうよ, quadratic residue、2冪非剰余を平方非剰余へいほうひじょうよ, quadratic non-residueといいます。

例題5.6.64

X² ≡ a (mod 13)

両辺の離散対数をとると、

2 log₂ X ≡ log₂ a (mod 12)

(2,12)=2より、平方剰余となるaに対応する指数log₂aは0,2,4,6,8,10の6個で、それに対応する既約剰余類、すなわち平方剰余は1,3,4,9,10,12の6個です。

ウィルソンの定理

次の定理はガウスの『整数論』によればウェアリングによって最初に公表されたものですが、ウィルソンWilson, John, 1741-1793の功績とされ、1771年にラグランジュによって始めて証明されました。このとき、オイラーがラグランジュからウィルソンの定理に関する二種類の証明を受け取ったときに、オイラーは原始根を使った証明をラグランジュに返送しました。ここではそのオイラーの証明を紹介することにします。

定理5.6.67 ウィルソンの定理

pを素数とするとき、

(p－1)! ≡ －1 (mod p)

証明

法pの原始根をrとすれば、

(p－1)! ≡ r^{1+2+ ⋯ + (p－2)} ≡ r^{(p－1)(p－2)/2} (mod p)

ここで、rの位数はp－1であるから、(r^(p－1)/2)²≡1(mod p), r^(p－1)/2≢1(mod p)となり、r^(p－1)/2の位数は2である。法pの既約剰余類群は位数p－1の巡回群であるから、位数2の元はϕ(2)=1個しか存在せず、－1は位数2であるからr^(p－1)/2≡－1(mod p)であり、

(p－1)! ≡ (－1)^p－2 ≡ －1 (mod p)

■

nが合成数であるときn=ab, a > 1, b > 1と書けます。このとき、

a | (n－1)!, b | (n－1)!

であり、一般にm>1のとき(m,m+1)=1ですから、

a ∤ (n－1)!+1, b ∤ (n－1)!+1

から

n ∤ (n－1)! +1 ⇔ (n－1)! ≢ －1 (mod n)

が成り立ちます。これを素数判定法としてまとめておきます。

命題5.6.70 ウィルソンの素数判定法

nが素数である必要十分条件は、

(n－1)! ≡ －1 (mod n)

この条件で素数であるかどうか判定するには階乗の計算が必要になるため、実際にはあまり使われません。

参考文献

[1] カール・フリードリヒガウス, ガウス整数論, 朝倉書店, 1995

[2] 高木貞治, 初等整数論講義第2版, 共立出版, 1971

[3] 遠山啓, 初等整数論, 日本評論社, 1972

[4] 河田敬義, 数論―古典数論から類体論へ, 岩波書店, 1992

[5] アンドレヴェイユ, 数論―歴史からのアプローチ, 日本評論社, 1987

人　　物

ウィルソン Wilson, John, 1741-1793

数　　学

原始根げんしこん, primitive root
離散指数りさんしすう, discrete exponentioal
底てい, base
離散対数りさんたいすう, discrete logarithm
直積分解ちょくせきぶんかい, direct product decomposition
n冪剰余 nべきじょうよ, residue of n-th power
n冪非剰余 nべきひじょうよ, non-residue of n-th power
平方剰余へいほうじょうよ, quadratic residue
平方非剰余へいほうひじょうよ, quadratic non-residue

Published by SANENSYA Co.,Ltd.