微分と代数方程式
著者:梅谷 武
語句:導関数,微分する,微分作用素,微分,二階導関数,n階導関数,有理関数体,形式的ローラン級数,代数方程式,根,解,零点,連立代数方程式,重複度,k重根,k位の零点,単根,重根,ルジャンドルの多項式
微分と代数方程式について述べる。
作成:2006-05-21
更新:2013-06-17
この節では可換環や整域・体上の多項式や形式的冪級数の微分を定義してその性質を調べます。本書では実数については触れませんが、実係数多項式を実関数と考えたときに極限の概念を使って定義される微分と、本節の代数的な性質だけで定義される微分とは代数的な議論をしている限りにおいてまったく同等です。歴史的に見れば形式的冪級数の収束性が議論されるようになって近代の解析学が誕生したという経緯もあり、多項式や形式的冪級数の微分を学ぶことは、代数計算の道具を準備するだけではなく、解析学を学ぶ準備という意味もあります。
可換環
R上の一変数多項式
f(X) = a0 + a1X + a2X2 + ⋯ + anXnと
Rの任意の元
αについて、
Xを
αに置き換えることによって、
Rの元
f(α) = a0 + a1α + a2α2 + ⋯ + anαnを定めることができます。これを
αを
f(X)に代入するといいます。
αに対して
f(α)を対応させることにより
f(X)を
R上の関数と考えることができます。
また、Xを別の多項式g(X)に置き換えることによって、多項式f(g(X)) = a0 + a1g(X) + a2g(X)2 + ⋯ + ang(X)nを定めることができます。これをg(X)をf(X)に代入するといいます。これはfとgをR上の関数と考えたときに関数の合成f∘gになっています。
同じようにn変数多項式f(X1,⋯,Xn)とRの元のn個の組(α1,⋯,αn)について、Xiにαiを代入することでRの元f(α1,⋯,αn)を定めることができます。(α1,⋯,αn)にf(α1,⋯,αn)を対応させることによりf(X1,⋯,Xn)をRのn個の直積Rn上の関数と考えることができますし、各変数を別の多項式に置き換えることによって、多項式の代入を定義することができます。
解答
a(X+h)+b = (aX + b) + ah,
(a(X+h)2 + b(X+h) + c) = (aX2 + bX + c)+(2aX + b)h + ah2.■
次の二つの多項式の和と積に関する微分の公式は基本的です。
可換環上の任意の一変数多項式
f,gについて次が成り立つ。
| (和)
| (f + g)' = f' + g' |
| (積)
| (fg)' = f'g + fg' |
証明
(D1) f(X+h) + g(X+h) = (f(X)+g(X)) + (f'(X)+g'(X))h + (⋯)h2,
(D2) f(X+h)g(X+h) = (f(X)+f'(X)h)(g(X)+g'(X)h) + (⋯)h2 = f(X)g(X) + (f'(X)g(X)+f(X)g'(X))h + (⋯)h2.■
これより任意個の多項式の和と積に関する微分の公式が導かれます。
可換環上の任意の一変数多項式
f1,⋯,fnについて次が成り立つ。
| (和)
| (f1 + ⋯ + fn)' = f1' + ⋯ + fn' |
| (積)
| (f1 f2 ⋯ fn)' = f1'f2 ⋯ fn + f1 f2' ⋯ fn + ⋯ + f1 f2 ⋯ fn' |
これを適用すると次の形の単項式の微分が計算できます。
可換環上の任意の一変数多項式
f=∑i=0naiXiについて次が成り立つ。
証明
各項について積の微分公式を適用して(aiXi)'=iaXi-1、全体を和の微分公式に当てはめれば結論が得られる。■
また多項式を代入した形の微分公式も得られます。これは解析学における合成関数の微分公式に相当します。
可換環上の任意の一変数多項式
f,gについて次が成り立つ。
| (代入)
| (f(g(X))' = f'(g(X))g'(X) |
証明
f(X)が単項式の場合に示せば、和の公式から一般の場合が得られる。f(X)=aXnとする。積の公式より(a (g(X))n)' = na(g(X))n-1g'(X)が成り立つ。■
これらの系において、添え字や指数のiは自然数ですが、係数のiは自然数ではなく係数環の単位元1をi回足したものを意味しています。これは場合によっては係数環の0となることもあります。n次多項式の微分はn-1次以下の多項式になりますが、ちょうどn-1次
になるかどうかはわかりません。
多変数の多項式環
R[X1,⋯,Xn]においても、一つの変数
Xiに着目して、
R[X1,⋯,Xi-1,Xi,Xi+1,⋯,Xn] = R[X1,⋯,Xi-1,Xi+1,⋯,Xn][Xi]と一変数多項式環と考えることによって、微分作用素
を定義することができます。
例えば
aX2 + bXY + cY2∈R[X,Y], a,b,c∈Rについて、変数
Xに関する微分をしてみます。
変数
Yに関する微分をしてみます。
となります。変数
Xに関する微分と変数
Yに関する微分を組み合わせてみます。
とすると
となります。この二つの微分作用素は、多項式に作用する順番が違っています。
体
k上の多項式環
k[X]は整域ですから、その商体を考えることができます。それを
k(X)と書き、
k上の
有理関数体ゆうりかんすうたい, rational function fieldといいます。これは
k[X]の元を分母と分子とする分数全体の集合
| Frac(k[X]) = | 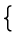 | | 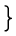 |
|
において
fg1=f1gのとき
とする同値関係
∽を考え、その同値類の集合
k(X) = Frac(k[X])/∽において、
f∈k[X]を
と同じとみなすことによって
k[X]⊂k(X)と考え、
k(X)上に次のような加法と乗法を定義したものでした。
多項式環
k[X]における微分の定義を有理関数体
k(X)へ、
によって拡張します。これについて次の微分公式が成り立ちます。
体
k上の有理関数体
k(X)の任意の元
f,gについて次が成り立つ。
| (和)
| (f+g)' = f'+g' |
| (積)
| (fg)' = f'g + fg' |
| (商)
| 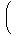 | | 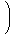 | | = | |
|
体
k上の有理関数体
k(X)の任意の元
f1,⋯,fnについて次が成り立つ。
| (和)
| (f1 + ⋯ + fn)' = f1' + ⋯ + fn' |
| (積)
| (f1 f2 ⋯ fn)' = f1'f2 ⋯ fn + f1 f2' ⋯ fn + ⋯ + f1 f2 ⋯ fn' |
体
k上の有理関数体
k(X)の任意の元
f,gについて次が成り立つ。
| (代入)
| (f(g(X))' = f'(g(X))g'(X) |
整域
R上の形式的冪級数環
R[[X]]を考えます。
0でない
Rの元
aについて
より、
(1-aX)は
R[[X]]の可逆元であり、その逆元は
∑i=0∞(aX)iです。同じようにして定数項が
0であるような多項式
f(X) ∈R[X]に対して
より、
(1-f(X))は
R[[X]]の可逆元であり、その逆元は
∑i=0∞(f(X))iです。それでは
f(X)が定数項が
0であるような形式的冪級数である場合はどうでしょうか。
この場合、各項が多項式ではなくて形式的冪級数となりますので、
という表現が本当に意味をもつのかどうかということが心配になりますが、
f(X)の定数項が
0であることから
(f(X))iは
i次より小さい項はすべて
0となり、任意の自然数
nに対して
n次の項をもつ可能性があるのは
(f(X))i, i=0,1,⋯,nだけですから問題ありません。一般に次のことが成り立ちます。
整域
R上の形式的冪級数環
R[[X]]において、定数項が
0でない形式的冪級数
f(X)について
(1-f(X))は
R[[X]]の可逆元であり、その逆元は
∑i=0∞(f(X))iである。
この命題によって、定数項a0が可逆元であるような形式的冪級数は、定数項が0の形式的冪級数f(X)によってa0(1-f(X))と書けますので、可逆元になることがわかります。また、R[[X]]の任意の可逆元∑i=0∞aiXiについて、その逆元∑i=0∞biXiとの積の定数項はa0 b0 = 1となりますから、a0は可逆元です。
整域
R上の形式的冪級数環
R[[X]]の元が可逆元であるかどうかは、その定数項が可逆元であるかどうかで定まる。
体k上の形式的冪級数環k[[X]]で考えると形式的冪級数が可逆であるかどうかは、その定数項が0かどうかで決まります。k[[X]]の商体をk((X))と書くことにします。これまでの議論からk[[X]]の0以外の可逆でない元はある正の整数nが存在してXn ∑i=0∞aiXi, a0≠0と書くことができます。ですから、Xnの逆元をX-nと書くことにすれば、k((X))はk[[X]]に{X-n | n > 0}を付け加えたものと考えることができます。
k[[X]]の元は(ai)i∈ℕという自然数を添え字とする数列でしたが、k((X))の元は(ai)i∈ℤという整数を添え字とし、ある整数n>0について-nより小さい添え字iについてai=0となるものとみなせば、形式的冪級数環の加法と乗法とを自然に拡張することができます。
体
k上の形式的冪級数環
k[[X]]の商体
k((X))の元は次のように書くことができる。
また、加法と乗法は次のように定義される。
形式的冪級数
f(X)=∑i=0∞ ai Xi ∈k[[X]]の微分は多項式の微分を自然に拡張するように
によって定義します。さらに微分の定義を形式的冪級数環
k[[X]]からその商体
k((X))へ、
によって拡張します。これにより
k((X))においても和や積の微分公式が成り立ち、形式的ローラン級数の微分は、
と書くことができます。
形式的冪級数の微分に関しても多項式と同じ微分公式が成り立ちます。
体
k上の形式的冪級数環
k[[X]]の任意の元
f,gについて次が成り立つ。
| (和)
| (f+g)' = f'+g' |
| (積)
| (fg)' = f'g + fg' |
| (商)
| 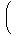 | | 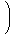 | | = | |
|
体
k上の形式的冪級数環
k[[X]]の任意の元
f1,⋯,fnについて次が成り立つ。
| (和)
| (f1 + ⋯ + fn)' = f1' + ⋯ + fn' |
| (積)
| (f1 f2 ⋯ fn)' = f1'f2 ⋯ fn + f1 f2' ⋯ fn + ⋯ + f1 f2 ⋯ fn' |
体
k上の形式的冪級数環
k[[X]]の任意の元
fと定数項が
0である元
gについて次が成り立つ。
| (代入)
| (f(g(X))' = f'(g(X))g'(X) |
可換環
R上の
n変数多項式環
R[X1,⋯,Xn]の
m次多項式
f(X1,⋯,Xn)を
0とおいた方程式
を
n元
m次
代数方程式だいすうほうていしき, algebraic equationといいます。
f(α1,⋯,αn)=0なる
(α1,⋯,αn)をこの方程式の
根こん, root、
解かい, solutionあるいは
零点れいてん, zero pointといい、根を求めることを代数方程式を解くといいます。代数方程式が複数あるとき、
連立代数方程式れんりつだいすうほうていしき, simultaneous algebraic equationといいます。
連立代数方程式を解くことは各代数方程式の零点の共通部分を求めることです。
可換環
R上の一変数多項式
f(X)に定数
αを代入することについて考えます。
X-α ∈R[X]は単多項式ですから、可換環上の多項式環における除法の原理より、
| f(X) = (X - α)q(X) + r, r ∈k
|
と書くことができます。両辺に
αを代入すると
f(α)=rとなり、
f(α)は
f(X)を
(X-α)で割った余りに等しいことがわかります。特に
αが
f(X)=0の根のときは
r=0で
f(X) = (X - α)q(X)と書くことができます。この性質は一元代数方程式の解法の基本となるものですので定理としてまとめておきます。
可換環
R上の一変数多項式
f(X)と
Rの元
αについて、
αが
f(X)=0の根であれば
(X-α)|f(X)であり、逆に
(X-α)|f(X)であれば
αは
f(X)=0の根である。
f(α) = an αn + ⋯ + a2 α2 + a1 α + a0を計算する。
| Step 1.
| f0 = 0 |
| Step 2.
| fi+1=fi α + an-iをi=0,⋯,nについて繰り返す。
|
| Step 3.
| f(α) = fn+1として終了する。
|
証明
演習とする。■
ホーナー法による計算例を示しておきます。
from Poly1 import *
a = Poly1( [-1,3,-3,1] )
b = Poly1( [1,1] )
print "a = ", a, ", b = ", b
print "a(-1) = ", a.Horner(-1), ", b(-1) = ", b.Horner(-1)
print "a(0) = ", a.Horner(0), ", b(0) = ", b.Horner(0)
print "a(1) = ", a.Horner(1), ", b(1) = ", b.Horner(1)
print
Poly1.SetChar( 'y' )
a = Poly1( [Fraction(-3,10), Fraction(1,25), Fraction(1,4)] )
b = Poly1( [Fraction(1,2), Fraction(-3,10)] )
print "a = ", a, ", b = ", b
print "a(-1) = ", a.Horner(-1), ", b(-1) = ", b.Horner(-1)
print "a(1/2) = ", a.Horner(Fraction(1,2)), \
", b(1/2) = ", b.Horner(Fraction(1,2))
print "a(0) = ", a.Horner(0), ", b(0) = ", b.Horner(0)
print "a(1) = ", a.Horner(1), ", b(1) = ", b.Horner(1)
a = X^3 - 3X^2 + 3X - 1 , b = X + 1
a(-1) = -8 , b(-1) = 0
a(0) = -1 , b(0) = 1
a(1) = 0 , b(1) = 2
a = 1/4y^2 + 1/25y - 3/10 , b = -3/10y + 1/2
a(-1) = -9/100 , b(-1) = 4/5
a(1/2) = -87/400 , b(1/2) = 7/20
a(0) = -3/10 , b(0) = 1/2
a(1) = -1/100 , b(1) = 1/5
require 'mathn'
require './poly1'
a = Poly1([-1, 3, -3, 1])
b = Poly1([1, 1])
print "a = ", a, ", b = ", b, "\n"
print "a(-1) = ", a.Horner(-1),
", b(-1) = ", b.Horner(-1), "\n"
print "a(0) = ", a.Horner(0),
", b(0) = ", b.Horner(0), "\n"
print "a(1) = ", a.Horner(1),
", b(1) = ", b.Horner(1), "\n"
print "\n"
Poly1.setchar('y')
a = Poly1([-3/10, 1/25, 1/4])
b = Poly1([1/2, -3/10])
print "a = ", a, ", b = ", b, "\n"
print "a(-1) = ", a.Horner(-1),
", b(-1) = ", b.Horner(-1), "\n"
print "a(1/2) = ", a.Horner(1/2),
", b(1/2) = ", b.Horner(1/2), "\n"
print "a(0) = ", a.Horner(0),
", b(0) = ", b.Horner(0), "\n"
print "a(1) = ", a.Horner(1),
", b(1) = ", b.Horner(1), "\n"
a = X^3 - 3X^2 + 3X - 1, b = X + 1
a(-1) = -8, b(-1) = 0
a(0) = -1, b(0) = 1
a(1) = 0, b(1) = 2
a = 1/4y^2 + 1/25y - 3/10, b = -3/10y + 1/2
a(-1) = -9/100, b(-1) = 4/5
a(1/2) = -87/400, b(1/2) = 7/20
a(0) = -3/10, b(0) = 1/2
a(1) = -1/100, b(1) = 1/5
次に一変数多項式f(X)の複数の根α1,⋯,αkが与えられた場合について考えます。上の定理により、各X-αi, i=1,⋯,kでf(X)は割り切れますが、それらの積(X-α1)⋯(X-αk)でf(X)を割る切れるでしょうか。これは係数環が整域という条件で成り立ちます。
整域
R上の一変数多項式
f(X)の相異なる根
α1,⋯,αkについて
(X-α1)⋯(X-αk)は
f(X)を割り切る。
証明
kに関する帰納法による。
k=1のときは前定理により成り立つ。
k-1のときに成り立つと仮定して
kのときに成り立つことを示す。仮定により、
| f(X) = (X-α1)⋯(X-αk-1)q(X)
|
と書ける。これに
αkを代入すると
| f(αk) = (αk-α1)⋯(αk-αk-1)q(αk) = 0
|
となるが、整域であるから
(αk-α1)⋯(αk-αk-1)は
0とは成り得ない。したがって
q(αk) = 0となり、前定理により
と書ける。これを上の式に代入すると
| f(X) = (X-α1)⋯(X-αk-1)(X-αk)qk(X)
|
となる。■
これによって整域上の一元代数方程式の根の個数はその次数を超えないことがわかります。
整域上の
0でない一変数
n次多項式は、一元
n次代数方程式として高々
n個の根しかもたない。
また、整域上の二つの多項式が一致するかどうかを調べるためには、その大きい方の次数をnとしたときに、n+1個の相異なる点での値が一致することを確かめればいいことがわかります。
整域上の
0でない次数
n以下の二つの一変数多項式は、
n+1個の相異なる点での値が一致すれば等しい。
証明
二つの多項式の差をとるとn+1個の点が根となっている。■
整域
R上の一変数多項式
f(X)の
k位の零点は、
f'(X)の高々
k-1位の零点である。
証明
f(X)=(X-α)k g(X)と書けるから、これに積の微分公式を適用すると
| | | k(X-α)k-1 g(X) + (X-α)k g'(X) |
|
| | | (X-α)k-1 ( kg(X) + (X-α)g'(X) ) |
|
となる。■
特に整域R上の一変数多項式f(X)の単根は、その導関数f'(X)の根になることはありません。
from Poly1 import *
f = Poly1( [-1,0,1] )
for n in range( 1, 8, 1 ):
a = f**n
fact = 1
for i in range( 1, n + 1, 1 ):
fact = fact * i
coef = Fraction( 1, 2**n * fact )
a = Poly1( [ coef ] ) * a.diff( n )
print n, a
1 X
2 3/2X^2 - 1/2
3 5/2X^3 - 3/2X
4 35/8X^4 - 15/4X^2 + 3/8
5 63/8X^5 - 35/4X^3 + 15/8X
6 231/16X^6 - 315/16X^4 + 105/16X^2 - 5/16
7 429/16X^7 - 693/16X^5 + 315/16X^3 - 35/16X
require 'mathn'
require './poly1'
f = Poly1([-1, 0, 1])
for n in 1...8
a = f**n
fact = 1
for i in 1..n
fact = fact * i
end
coef = 1 / (2**n * fact)
a = Poly1([coef]) * a.diff(n)
print n, " ", a, "\n"
end
1 X
2 3/2X^2 - 1/2
3 5/2X^3 - 3/2X
4 35/8X^4 - 15/4X^2 + 3/8
5 63/8X^5 - 35/4X^3 + 15/8X
6 231/16X^6 - 315/16X^4 + 105/16X^2 - 5/16
7 429/16X^7 - 693/16X^5 + 315/16X^3 - 35/16X
人 物
ホーナー Horner, William George, 1786-1837
イギリスの数学者。1819年にホーナー法を発表するが、その150年前の1669年に出版されたアイザック・ニュートン(Sir Isaac Newton, 1642-1727)の著書にすでにその方法が記されている。
数 学
導関数 どうかんすう, derived function, derivative
微分する びぶんする, differentiate
微分作用素 びぶんさようそ, differential operator
一変数の微分作用素は通常d/dxと書かれることが多いが、具象数学階梯においては、∂ で微分作用素を表わし、d という記号は接ベクトルの成分や微分形式を表わすときにのみ使用し、二つの概念を明確に区別する。
微分 びぶん, derivation
二階導関数 にかいどうかんすう, second derivative
n階導関数 nかいどうかんすう, n-th derivative
有理関数体 ゆうりかんすうたい, rational function field
形式的ローラン級数 けいしきてきろーらんきゅうすう, formal Laurent series
代数方程式 だいすうほうていしき, algebraic equation
根 こん, root
解 かい, solution
零点 れいてん, zero point
連立代数方程式 れんりつだいすうほうていしき, simultaneous algebraic equation
重複度 ちょうふくど, multiplicity
k重根 kじゅうこん, k-ple root
k位の零点 kいのれいてん, zero point of order k
単根 たんこん, simple root
重根 じゅうこん, multiple root
ルジャンドルの多項式 るじゃんどるのたこうしき, Legendre's polynomial