イデアル
著者:梅谷 武
語句:イデアル,加群,R-加群,単項イデアル,上界,最小上界,上限,下界,最大下界,下限,束,モジュラー束
イデアルについて述べる。
作成:2006-04-24
更新:2013-06-14
整数aの倍数全体の集合ℤa={na|n∈ℤ}について考えます。この集合は整数の部分集合として特別な性質をもっています。そしてその性質は整数論を学んでいくにあたってとても重要なものになります。そこでこれからその性質について調べていくことにしましょう。
可換環
Rの空でない部分集合
Iが次の性質をもつとき
イデアルいである, idealという。特に
Rと
{0}はイデアルである。
| (I1)
| a, b ∈ I ⇒ a + b ∈ I |
| (I2)
| r ∈ R, a ∈ I ⇒ ra ∈ I |
Iを可換環
Rのイデアルとするとき、
a,b ∈ I ⇒ a - b ∈ I
証明
Rの乗法の単位元1の加法に関する逆元-1について-b=(-1)bなのでa-b=a+(-1)b∈I.■
この命題によりイデアルは加法に関して閉じていて、零元や加法に関する逆元も含まれていることがわかります。これはイデアルがRの加法に関する部分群となっていることを示しています。イデアルが単なる部分加法群と異なるのはRの係数倍に関しても閉じていることです。このような加法群はR-加群と呼ばれる重要な代数的構造です。このR-加群の概念をここで定義しておくことにしましょう。
可換環
Rが加法群
Mに作用している、すなわち写像
R×M → M, (r,m) ↦ rmが定義され、それが次の性質をもつとき
Mを
R上の
加群かぐん, module、あるいは
R-加群R-かぐん, R-moduleという。
| (1)
| a(x + y) = ax + ay, a ∈ R, x,y ∈ M |
| (2)
| (a + b)x = ax + bx, a,b ∈ R, x ∈ M |
| (3)
| (ab)x = a(bx), a,b ∈ R, x ∈ M |
| (4)
| 1x = x, 1 ∈ R, x ∈ M |
また、イデアルは乗法に関しても閉じていて部分環にもなっていますが、イデアルは部分環よりも強い概念です。
Iを可換環
Rのイデアルとし、
ai∈I, i=1,⋯,nとすると
| r1 a1 + r2 a2 + ⋯ + rn an ∈ I, ri ∈ R
|
証明
(I2)から任意のiについてri ai ∈ I。(I1)によりこれらの和はIに
含まれる。■
可換環
Rの元
ai, i=1,⋯,nが生成するイデアルを
| (a1, ⋯, an) = { r1 a1 + ⋯ + rn an | ri ∈ R }
|
と定義します。
ai, i=1,⋯,nを含むイデアルは
r1 a1 + ⋯ + rn anの形の元をすべて含まなければなりませんが、この形の元全体の集合自体がイデアルになっています。イデアルを
R-加群と考えた場合、
(a1, ⋯, an)は生成系
{a1, ⋯, an}から
生成された
R-加群であるといいます。このイデアルは
ai, i=1,⋯,nを含むイデアルの中で最小のものという性質をもっています。
可換環
Rのイデアル
I,Jについて
I∩Jはイデアルとなる。
証明
r∈R, a∈I∩Jについてra, a + b∈I∩J.■
Rのイデアル全体の集合に和と積を定義します。
I,Jを
Rのイデアルとしたとき、
と定義します。
可換環
Rのイデアル
I,Jについて
I+Jはイデアルとなる。
証明
r∈R, a+b, a'+b'∈I+Jとするとr(a+b)=ra+rb, (a+a')+(b+b')∈I+J.■
可換環
Rのイデアル
I,Jについて
IJはイデアルとなり、
IJ ⊂ I∩Jである。
証明
r∈R, ab,a'b'∈IJとするとr(ab)=(ra)b∈IJであり、定義より和について閉じている。また、ab∈IJならばあきらかにab∈I∩J.■
可換環
Rのイデアル
Iが単元を含めば
I=Rである。したがって
Rが体のときはイデアルは
Rと
{0}という自明なものしかない。
証明
単元を含めばその逆元をかけることで単位元1がIに含まれることになり、r∈Rとすればr1=r∈I.■
特に
a,bを
Rの元としたとき、それらから生成されるイデアルについて
が成り立ちます。
可換環
Rの任意の
0でない元
aについて
| (a) = Ra = { ra | r ∈ R }
|
はイデアルとなりますが、これを
aによって生成される
単項イデアルたんこういである, principal idealといいます。整数
aの倍数全体の集合
(a)=ℤaは単項イデアルです。整数にはすべてのイデアルが単項イデアルになるという特別の性質があります。つまり、すべてのイデアルがある数の倍数の集合と一致してしまうのです。これはいろいろな可換環を調べていくとかなり特別な性質であることがわかります。後に多変数多項式環や二次体の整数が導入される際に単項イデアルではないイデアルの例が示されることになるでしょう。
一般に可換環Rにおいてすべてのイデアルが単項イデアルになるとき、Rを単項イデアル環といいます。有理整数と一変数多項式環はともに単項イデアル環であって、さらに除法の原理が成り立つという特徴をもっており、そのために両者の理論には共通点が多く見られます。次章において一変数多項式環の性質が有理整数とほとんど同じようにして証明されることを見るでしょう。
証明
I⊂ℤを任意のイデアルとする。もし
I={0}であれば
I=(0)であるから単項イデアルである。
I≠{0}としよう。
0≠n∈Iがもし負の数であれば、
-n∈Iより
I∩ℕ≠∅である。この最小元を
bとすると
(b)⊂Iである。
Iの任意の元
aについて
を成り立たせる整数
q,rがただ一組だけ存在する。
a, bq∈Iより
r=a-bq∈Iとなるが、ここでもし
r≠0ならば
0<r<bとなり、
bが最小であることに矛盾する。したがって
r=0である。
a=bq∈(b)となり、
(b)=Iであることが示された。■
さて、整数
a,bの公倍数全体の集合は
(a)∩(b)ですが、これはまたイデアルですからその生成元
lが存在して
(l)=(a)∩(b)となります。このとき
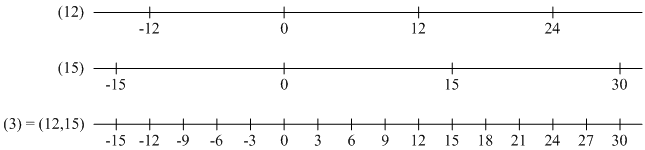
l=lcm(a,b)となっています。例えば
12と
15の場合、
図2.3.2が示すように
(12)∩(15)=(60)です。
最小公倍数をあるイデアルの生成元として得ることができましたが、最大公約数も同じようにあるイデアルの生成元として得ることができます。二つの整数a,bから生成されるイデアル(a,b)は単項イデアルですから(d)=(a,b)=(a)+(b)となる正整数dが存在します。このときd=gcd(a,b)となっています。例えば12と15の場合、下の図が示すように(12)+(15)=(3)です。
有理整数が単項イデアル整域であることの証明を見ればわかるように、最大公約数d=gcd(a,b)は集合(a,b)∩ℕ = {xa + yb|x,y∈ℤ}∩ℕの最小元として求められます。これは2元方程式ax+by=dを満たす整数の組(x,y)を求めていることに他なりません。
ここで一般的な順序集合
(A,≦)について考えます。
Aの二つの元
x,yについて
z≧x, z≧yなる
zを
x,yの
上界じょうかい, upper boundといいます。また
x,yの上界の集合が最小元
zをもつとき、すなわち任意の
x,yの上界
wに対して
z≦wとなるとき、その最小元を
最小上界さいしょうじょうかい, least upper boundあるいは
上限じょうげん, supremumといいます。
x,yの上限を
x∨yと書くことにします。同じように
Aの二つの元
x,yについて
z≦x, z≦yなる
zを
x,yの
下界かかい, lower boundといいます。また
x,yの下界の集合が最大元
zをもつとき、すなわち任意の
x,yの下界
wに対して
z≧wとなるとき、その最大元を
最大下界さいだいかかい, greatest lower boundあるいは
下限かげん, infimumといいます。
x,yの下限を
x∧yと書くことにします。
順序集合においてその任意の2元の上限と下限が存在するときその順序集合を
束そく, latticeといいます。順序集合
(A,≦)において順序の定義を逆にしたもの、すなわち、
x≦yのとき
x≧'yと定義したもの
(A,≧')はまた順序集合となります。これを双対な順序集合といいます。双対な順序集合においては上界と下界、上限と下限の概念が逆になります。このことから束に関するある命題が成り立つときには、その命題において上界と下界、上限と下限の概念を入れ替えた命題も成り立つことがわかります。これを束の双対性といいます。
順序集合
(ℕ,|)は束です。自然数
a,bに対して、
となっています。可換環
Rのイデアル全体の集合を
ℑ(R)で表すことにすると順序集合
(ℑ(R),⊆)は束になります。
Rのイデアル
I,Jに対して、
となっています。このような準備の下でこの節の内容は次の定理にまとめられます。
(ℕ,|)と
(ℑ(ℤ),⊆)は
aに対して
(a)を対応させる写像によって1対1に対応する。この写像は順序を逆に写し、二つの束は双対となる。
(ℕ,|)と
(ℑ(ℤ),⊆)は単なる束ではなくて、モジュラー束と呼ばれるものになっています。
モジュラー束もじゅらーそく, modular latticeとは
| (モジュラー律)
| x≦zならば任意のyについて、(x∨y)∧z = x∨(y∧z) |
という性質を満たす束のことです。modularは加群と訳されているmoduleの形容詞です。moduleとは後に導入される数の合同概念における法の意味ですが、加法群の意味でも使われます。この加法群の部分群の集合でモジュラー律が成り立つことからモジュラー束と名付けられました。可換環のイデアルの集合の他に群の正規部分群の集合、線形空間の部分空間の集合、射影空間の部分空間の集合などもモジュラー束になります。
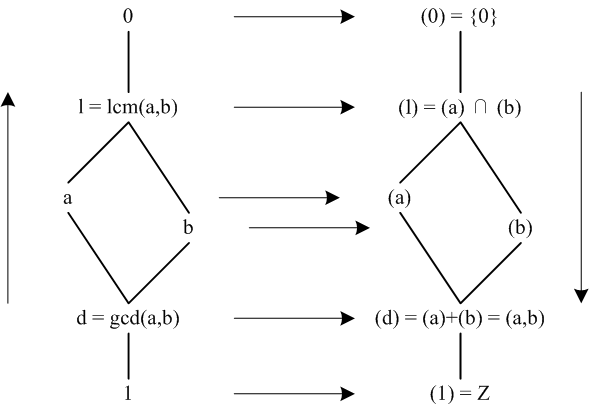
モジュラー束にはその任意の2元
a,bについて、閉区間
[a, a∨b]と
[a∧b, b]において、写像
が部分束としての1対1対応を与えるという著しい特徴があります。ここでは
12と
15の場合の例を図示することにとどめ、詳細についてはこれ以上は触れません。下の図において平行四辺形の対辺にあたる区間どうしが1対1に対応しています。
数 学
イデアル いである, ideal
加群 かぐん, module
R-加群 R-かぐん, R-module
単項イデアル たんこういである, principal ideal
上界 じょうかい, upper bound
最小上界 さいしょうじょうかい, least upper bound
上限 じょうげん, supremum
下界 かかい, lower bound
最大下界 さいだいかかい, greatest lower bound
下限 かげん, infimum
束 そく, lattice
モジュラー束 もじゅらーそく, modular lattice
![[15,60]と[3,13]、[3,15]と[12,60]の同型対応](figure/figure_206.gif)