最小公倍数
著者:梅谷 武
語句:公倍数,最小公倍数
語句:公倍数,最小公倍数
最小公倍数とその最大公約数との関係について述べる。
作成:2006-04-24
更新:2013-06-16
更新:2013-06-16
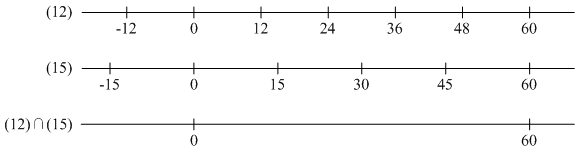
整数mが二つの整数a,bについてa|m,b|mとなっているときmをa,bの公倍数こうばいすう, common multipleといいます。整数aの倍数全体の集合はℤa={na|n∈ℤ}一致し、無限集合になります。これを(a)と書くことにします。a,bの公倍数全体の集合は(a)∩(b)となり、これも無限集合です。この集合と自然数全体の集合との共通部分の最小元、つまり正の公倍数の最小のものをaとbの最小公倍数さいしょうこうばいすう, least common multipleといい、lcm(a,b)と書くことにします。例えば12と15の場合、lcm(12,15)=60となります。
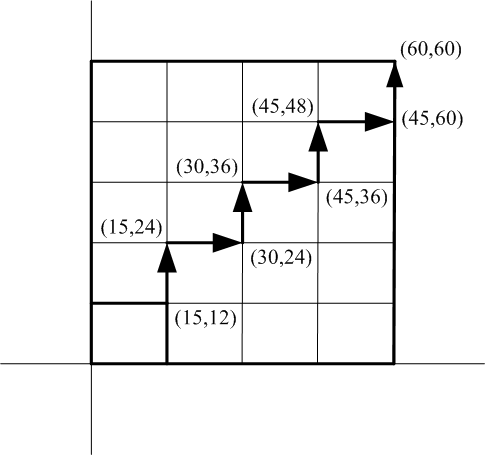
下の図に示すように二つの整数a,bの最小公倍数を求めるという問題は辺の長さがa,bである長方形のタイルを使って埋め尽くすことができる正方形の辺の長さの最小値を求めるという幾何学の問題に置き換えることができます。
二つの整数の最小公倍数を求めるためにユークリッド算法の逆を行ってみるという発想がまず浮かんできます。つまり、長方形のタイルの辺が短い方向に長い辺を超えるまでタイルを置いていって、もし長い辺と等しくなればちょうど正方形になり、長い辺よりも大きくなれば直交方向にタイルを置いていくということを繰り返すというものです。
これは算法としては倍数の集合を小さい順にすべて調べていくよりはずっと効率がいいやり方です。長方形のタイルの辺が短い方向に長い辺を超えるまでタイルを置いていくという操作は、式で表現すれば
a>bのときa=bq+rを計算し、余りrが0でなければ
とすることです。
| a = b(q+1) - r, 0≦r<|b| |
算法2.3.7 ユークリッドの互除法の逆
二つの正整数a,bの最小公倍数lを求める。| Step 1. | s=a, t=bとおく。 |
| Step 2. | sをtで割った余りrを求める。(s=tq+r, 0≦r<|b|) |
| Step 3. | もしr=0であればl=sとして終了する。 |
| Step 4. | s=t(q+1)とし、もしtがbと等しいならt=b、そうでないならt=aとして、Step 2.へ。 |
しかし、これを実際にプログラミングしてみるとわかりますがあまり実用的な算法とはいえません。最小公倍数の求め方としては次の公式によって最大公約数を求めることに帰着させる方法がすぐれています。
この命題は有理整数の基本定理を使うと簡単に証明できますので、それまで証明は保留にしておきます。ここでは最小公倍数を求める二つの算法をプログラミングし、その実行時間を比較してみましょう。
sample2.3.1.py
from time import * def gcd( a, b ): while b != 0: r = a % b a = b b = r if a < 0: return -a else: return a def lcm( a, b ): if ( a == 0 ) or ( b == 0 ): return 0 if a < 0: a = -a if b < 0: b = -b s = a t = b while 1: r = s % t if r == 0: break s = (s - r) + t if t == b: t = a else: t = b return s a = 23423553; b = 12312313 t1 = clock() d = gcd( a, b ) if d == 0: e = 0 else: e = a * b / d if e < 0: e = - e t2 = clock() l = lcm( a, b ) t3 = clock() print '1. lcm( %d, %d ) = %d, time = %d[s]' % ( a, b, e, (t2 - t1) ) print '2. lcm( %d, %d ) = %d, time = %d[s]' % ( a, b, l, (t3 - t2) )
sample2.3.1.pyの実行結果
1. lcm( 23423553, 12312313 ) = 288398116108089, time = 0[s] 2. lcm( 23423553, 12312313 ) = 288398116108089, time = 16[s]
sample2.3.1.rb
def gcd(a, b) while b != 0 r = a % b a = b b = r end if a < 0 return -a else return a end end def lcm(a, b) if (a == 0) or (b == 0) return 0 end if a < 0 a = -a end if b < 0 b = -b end s = a t = b while 1 r = s % t if r == 0 break end s = (s - r) + t if t == b t = a else t = b end end return s end a = 23423553; b = 12312313 t1 = Time.now() d = gcd(a, b) if d == 0 e = 0 else e = a * b / d end if e < 0 e = - e end t2 = Time.now() l = lcm(a, b) t3 = Time.now() printf "1. lcm(%d, %d) = %d, time = %d[s]\n", a, b, e, (t2 - t1) printf "2. lcm(%d, %d) = %d, time = %d[s]\n", a, b, l, (t3 - t2)
sample2.3.1.rbの実行結果
1. lcm(23423553, 12312313) = 288398116108089, time = 0[s] 2. lcm(23423553, 12312313) = 288398116108089, time = 18[s]
ユークリッドの互除法を使う方が圧倒的に速いことがわかります。このように実際に計算機を使って計算を行う場合に、算法の選択やプログラミングの仕方の違いによって計算時間に大きな違いがでてくることがよくあります。
Published by SANENSYA Co.,Ltd.