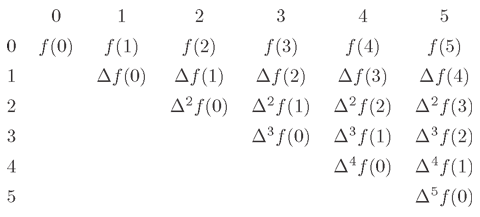行列と反転公式
著者:梅谷 武
語句:アイザック・ニュートン,線形空間,ベクトル空間,ベクトル,スカラー,線形結合,線形従属,線形独立,部分空間,基底,次元,差分,n階差分,線形写像,線形作用素,和分,ニュートン級数
行列と反転公式について述べる。
作成:2006-05-29
更新:2021-03-17
4.6 行列と反転公式
 本書においては線形代数を体系的に述べることができませんが、いろいろな数式を行列で表現することで、計算の見通しが良くなるだけでなく、複雑な計算を機械的に行う仕組みとしても便利ですので、ここで簡単に紹介しながら、その例として二項係数やスターリング数の反転公式について触れておきます。
 有理数体ℚ上の多項式環ℚ[X]はℚ-加群ですが、一般に体上の加群を線形空間せんけいくうかん, linear spaceあるいはベクトル空間べくとるくうかん, vector spaceといいます。ベクトル空間においては、その元をベクトルべくとる, vector、係数体の元をスカラーすからー, scalarと呼びます。ℚ[X]をℚ上のベクトル空間と考えた場合、多項式はベクトルで、有理係数はスカラーということになります。
 ベクトル空間のn個のベクトルx1,⋯,xnに対して、係数a1,⋯,anをかけて和をとったもの
a1 x1 + ⋯ + an xn
を線形結合せんけいけつごう, linear combinationあるいは一次結合といいます。
a1 x1 + ⋯ + an xn = 0
となるすべてが0ではない係数a1,⋯,anが存在するとき、n個のベクトルからなる集合{x1,⋯,xn}は線形従属せんけいじゅうぞく, linearly dependentあるいは一次従属であるといいます。そうでないとき、すなわち、
a1 x1 + ⋯ + an xn = 0 ⇒ a1 = ⋯ = an = 0
が成り立つとき、線形独立せんけいどくりつ, linearly independentあるいは一次独立であるといいます。
 ベクトル空間の部分集合が加法と係数倍に関して閉じているとき、それを部分空間ぶぶんくうかん, subspaceといいます。これは体上の加群と考えたときの部分加群の概念と一致します。{x1,⋯,xn}が生成する部分空間とは、その線形結合の全体の集合が成す部分空間のことをいいます。これは{x1,⋯,xn}を含む最小の部分空間としても特徴付けられます。
 ベクトル空間が線形独立なn個のベクトルからなる集合{x1,⋯,xn}から生成されているとき、{x1,⋯,xn}をそのベクトル空間の基底きてい, basisといい、基底に含まれるベクトルの個数をそのベクトル空間の次元じげん, dimensionといいます。

反転公式

 この節で考えるベクトル空間Vはℚ[X]のn次以下の多項式全体の集合です。{1, X, X2, ⋯, Xn}はVの基底になっていますから、Vの次元はn+1です。不定元Xの昇階乗の集合{ 1, X1, X2, ⋯, Xn }を考えてみましょう。Xiはi次の多項式ですから、この集合は一次独立で、ベクトル空間の次元は一定であることから、これもまたVの基底になっていることがわかります。
 第1種スターリング数の定義式から、
Xi =
i
∑
j=0
[i
j		]
Xj
, i=0,1,2,⋯,n
が成り立ちますが、これを行列を使って表現すると次のようになります。
lb192
1
X1
X2
⋮
Xn
rb192 = lb288
1
0
0
⋯
0
0
[1
1		]
0
⋯
0
0
[2
1		]
[2
2		]
⋯
0
⋮
⋮
⋮
⋱
0
0
[n
1		]
[n
2		]
⋯
[n
n		]
rb288 lb192
1
X
X2
⋮
Xn
rb192
同じように冪乗を昇階乗で表わす公式：
Xi =
i
∑
j=0
(－1)i－j
{i
j		}
Xj
, i=0,1,2,⋯,n
を行列を使って表現すると次のようになります。
lb192
1
X
X2
⋮
Xn
rb192 = lb288
1
0
0
⋯
0
0
{1
1		}
0
⋯
0
0
(－1)
{2
1		}
{2
2		}
⋯
0
⋮
⋮
⋮
⋱
0
0
(－1)n－1
{n
1		}
(－1)n－2
{n
2		}
⋯
{n
n		}
rb288 lb192
1
X1
X2
⋮
Xn
rb192
前の式に後の式の行列を左からかけることによって、n≧i,j≧0なる整数i,jについて
Xi =
i
∑
j=0
i
∑
k=0
(－1)i－k
{i
k		}
[k
j		]
Xj
となりますが、{1, X, X2, ⋯, Xn}の線形独立性より、
i
∑
k=0
(－1)i－k
{i
k		}
[k
j		]
 = lc48
1,
i=j
0,
i≠j
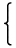であることがわかります。すなわち、前の行列と後の行列をかけたものは単位行列になっています。言い換えれば、この二つの行列は二つの基底を相互に変換し、互いに他の逆行列になっています。このことを数式で表現しているのが次の反転公式です。

命題4.6.8 スターリング数の反転公式

 正の整数nとn≧i,j＞0なる整数i,jについて次の式が成り立つ。
(4.1)
n
∑
k=1
(－1)n－k
{i
k		}
[k
j		]
=
δij = lc48
1,
i=j
0,
i≠j
(4.2)
n
∑
k=1
(－1)n－k
[i
k		]
{k
j		}
=
δij = lc48
1,
i=j
0,
i≠j
 次に{1, (X－1), (X－1)2, ⋯, (X－1)n}という単項式の集合を考えます。(X－1)iはi次の多項式ですから、この集合は一次独立で、これもまたVの基底になっています。二項定理からi=1,2,⋯,nについて
Xi = (1+(X－1))i
=
i
∑
j=0
(i
j		)
(X－1)j
(X－1)i
=
i
∑
j=0
(－1)i－j
(i
j		)
Xj
が成り立ちますから、二項係数においてもスターリング数と同様にi＜jのときは
(i
j		)
 = 0
と定義すれば、同じようにして次のような二項係数に関する反転公式が得られます。

命題4.6.10 二項係数の反転公式

 正の整数nとn≧i,j≧0なる整数i,jについて次の式が成り立つ。
(4.3)
n
∑
k=0
(－1)n－k
(i
k		)
(k
j		)
 = δij = lc48
1,
i=j
0,
i≠j
 反転公式は、例えば、x1,⋯,xnとy1,⋯,ynという二つの数列が
yi =
i
∑
j=0
[i
j		]
xj
, i=0,1,2,⋯,n
という関係になっている場合には、
xi =
i
∑
j=0
(－1)i－j
{i
j		}
yj
, i=0,1,2,⋯,n
によって、また、
yi =
i
∑
j=0
(i
j		)
xj
, i=0,1,2,⋯,n
という関係になっている場合には、
xi =
i
∑
j=0
(－1)i－j
(i
j		)
yj
, i=0,1,2,⋯,n
によって、既知のy1,⋯,ynから未知のx1,⋯,xnを求めるときに使います。
 これらの計算ではスターリング数や組み合わせの計算が必要になるようにみえますが、反転公式が成り立つような二つの数列を相互変換する場合にスターリング数や組み合わせの値を使わないで計算する方法があります。それがこの章の主題である三角形算術です。三角形算術はこのような数列の相互変換のための算法として特徴付けることができます。

差分と和分

 ここでは有理数の数列を自然数から有理数への関数f:ℕ→ℚと考え、f(n)で表わすことにします。数列f(n)の差分さぶん, differenceあるいは階差を
(4.4)
Δf(n) = f(n+1) － f(n)
によって定義します。数列に対してその差分をとる操作を続けることによって、n階差分nかいさぶん, difference of n-th orderを
(4.5)
Δnf(n) = Δn－1f(n+1) － Δn－1f(n)
によって定義します。n階差分もまた数列になっています。
 1階差分から順番に差分をとっていきますと
                    Δf(n)
=
f(n+1) － f(n)
Δ2f(n)
=
f(n+2) － 2f(n+1) + f(n)
Δ3f(n)
=
f(n+3) － 3f(n+2) + 3f(n+1) － f(n)
となりますが、一般に次の式が成り立ちます。

命題4.6.15

(4.6)
Δif(n) =
i
∑
j=0
(－1)i－j
(i
j		)
f(n + j)
 これを証明するために形式的冪級数環へ作用する作用素環の考え方を使ってみましょう。一般に体k上のベクトル空間Vから別のベクトル空間への写像φが、任意のa,b∈V,λ∈kに対して、
(1) φ(a+b) = φ(a)+φ(b)
(2) φ(λa) = λφ(a)
を満たすときφを線形写像せんけいしゃぞう, linear mapping、線形作用素せんけいさようそ, linear operatorといいます。
 ベクトル空間ℚ[[X]]から自分自身への作用素
E : ℚ[[X]] → ℚ[[X]], (f(n))n ∈ℕ ↦ (f(n+1))n ∈ℕ
を考えます。これは形式的冪級数を数列と考えると数列を一つずらす操作をする作用素です。ℚ上の任意の多項式P(X)=∑i=0naiXiにこの作用素Eを代入して新しい作用素を作ることができます。
P(E)f(n) =
n
∑
i=0
aif(n+i)
このようにしてℚ[E]はℚ[[X]]上の作用素から成る可換環になります。一般に関数の集合が作るベクトル空間上の作用素からなる環は作用素環と呼ばれます。有限次元のベクトル空間上の作用素環は行列が作る環として表現することができて一般には非可換です。
 さて命題の証明ですが、差分作用素はX－1にEを代入したものに他なりませんから、二項定理を使って
               Δif(n)
=
(E － 1)if(n)
=
i
∑
j=0
(－1)i－j
(i
j		)
Ejf(n)
=
i
∑
j=0
(－1)i－j
(i
j		)
f(n+j)
というように示されます。
 差分の逆の操作、つまりある数列が与えられたときに、差分をとるとその数列になるような数列を求める操作のことを和分わぶん, summationといいます。数列g(n)が与えられたときにΔf(n) = g(n)となるf(n)がg(n)の和分です。この場合、ある定数Cについてf(n)+Cという数列もg(n)の和分になりますので、和分は一意には定まりません。ここでは和分作用素ΣをX+1にEを代入したものとして定義することにします。そうすると上と同じように二項定理を使うことによって次の式を示すことができます。

命題4.6.20

(4.7)
Σif(n) =
i
∑
j=0
(i
j		)
f (n + j)
 不定元Xと自然数kに関する二項係数を
(X
k		)
 =
Xk
k!
によって定義します。Xに自然数を代入したときには通常の二項係数と一致します。冪乗を第2種スターリング数を使って降階乗の多項式で表わす式
Xn =
n
∑
k=0
{n
k		}
Xk
を、この記号によって
Xn =
n
∑
k=0
k!
{n
k		}
(X
k		)
と書くことにしましょう。これにより、任意の多項式f(X)=∑i=0naiXiは、
f(X) =
n
∑
i=0
bi
(X
i		)
と二項係数で展開するができます。これはアイザック・ニュートンNewton, Isac, 1642-1727がよく用いたのでニュートン級数にゅーとんきゅうすう, Newton seriesと呼ばれています。
Δ
(X
i		)
 =
(X+1
i		)
 －
(X
i		)
 =
(X
i－1		)
と定義すると
Δkf(X) =
n
∑
i=0
bi
(X
i－k		)
となります。
Δ
(X
0		)
 = 1
からi－kが負のときは
(X
i－k		)
 = 0
になります。 この式でXに0を代入するとΔkf(0) = bkとなりますから、差分によってニュートン 級数の係数を求めることができて、
f(X) =
n
∑
i=0
Δif(0)
(X
i		)
となります。したがって、数列f(n)がk次多項式f(X)によって表わされているときに、数列f(n)の第k階までの差分をとることによって、f(X)をニュートン級数に展開したときの係数を求めることができます。
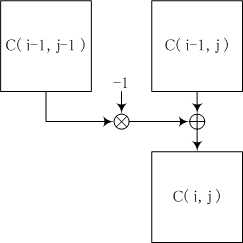
 差分と和分の関係式を満たす数列は三角形算術によって計算することができます。正の整数kについて数列f(n)のn=0におけるk階差分を求めます。まず、k+1 × k+1の桝目を用意して、その第0行にf(0),⋯,f(k)を入れます。i行j列の桝目をC(i,j)で表わすことにすれば、
C(0,j) = f(j), j=0,1,2,⋯,k
ということです。そして隣り合った桝目の差分を右側の桝目の下に入れていきます。
C(i,j) = C(i－1,j－1) － C(i－1,j), i=0,1,2,⋯,k, j=i,⋯,k
図4.6.23 生成規則
生成規則
 この操作が終わったときに対角線上にk階までの差分が入っています。
 この算法においてはk+1 × k+1の桝目が必要になるように思われますが、実際にはk+1個の桝目だけで十分です。それは第i行目を計算するとき、すなわち第i階差を求めるときに、jを第k列から始めて第i列で終わるような順番で計算すれば、その結果を第j列に重ね書きすることができます。
図4.6.26 差分の三角形
差分の三角形
 和分は差分の三角形で生成規則を
C(i,j) = C(i－1,j－1) + C(i－1,j), i=0,1,2,⋯,k, j=i,⋯,k
で置き換えるだけです。
 差分と和分の計算例として自然数列の0における9階差分をとり、次にその9階和分をとって元に戻してみます。作業領域としては長さが10のリストだけを使用します。

sample4.6.5.py

C = range( 10 )
print C
for i in range( 10 ):
  for j in range( 9, i, -1 ):
    C[j] = C[j] - C[j-1]
print C
for i in range( 10 ):
  for j in range( 9, i, -1 ):
    C[j] = C[j] + C[j-1]
print C

sample4.6.5.pyの実行結果

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

sample4.6.5.rb

C = (0...10).to_a
p C
for i in 0...10
  for j in ((i+1)..9).to_a.reverse
    C[j] = C[j] - C[j-1]
  end
end
p C
for i in 0...10
  for j in ((i+1)..9).to_a.reverse
    C[j] = C[j] + C[j-1]
  end
end
p C

sample4.6.5.rbの実行結果

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

ベルヌーイ数の算法

 形式的冪級数環ℚ[[X]]上の作用素として次のようなものを考えます。
X
∂
∂X
:f(X) =
∞
∑
i=0
aiXi
 ↦ Xf'(X) =
∞
∑
i=0
iaiXi
これを何度か作用させると
lb36
X
∂
∂X
rb36f(X)
=
Xf'(X)
lb36
X
∂
∂X
rb36
2
 f(X)
=
Xf'(X) + X2f(2)(X)
lb36
X
∂
∂X
rb36
3
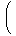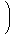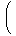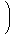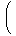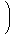 f(X)
=
Xf'(X) + 3X2f(2)(X) + X3f(3)(X)
となりますが、一般に次の式が成り立ちます。

命題4.6.34

(4.8)
lb36
X
∂
∂X
rb36
n
 f (X) =
n
∑
j=0
{n
j		}
Xjf(j)(X)

証明

 演習とする。■
 次にスターリング数の反転公式を利用して、ベルヌーイ数の計算公式Iを書き換えて、ベルヌーイ数の具体的な算法を示します。

命題4.6.37 ベルヌーイ数の計算公式II

(4.9)
Bk =
k
∑
j=0
(－1)jj!
j+1
{k+1
j+1		}
, k∈ℕ

証明

 第2種スターリング数の加法公式により、
{k+1
j+1		}
 =
{k
j		}
 + (j+1)
{k
j+1		}
を右辺に代入して、
k
∑
j=0
(－1)jj!
j+1
lb36
{k
j		}
 + (j+1)
{k
j+1		}
rb36
ここで
j! =
[j+1
1		]
とスターリング数の反転公式を使うと
=
k
∑
j=0
(－1)jj!
j+1
{k
j		}
 +
k
∑
j=0
(－1)j
[j+1
1		]
{k
j+1		}
=
k
∑
j=0
(－1)jj!
j+1
{k
j		}
 + δ1k
ベルヌーイ数の計算公式Iを使うと、これは(－1)kBk + δ1kとなるがk=1のときは－B1 + 1 = 1/2よりB1に等しく、k≠1のときは(－1)kBkとなるが、kを1より大きい奇数としたときBk = 0であるからBkに等しい。■
 有理数列(C(0,j)j∈ℕ)が与えられたときに、
C(i,j) = (j+1)( C(i－1,j) － C(i－1,j－1) ), i＞0, j∈ℕ
によって数列(C(i,j)j∈ℕ)を定めます。この母関数をpi(X) = ∑j=0∞C(i,j)Xjとすると
pi(X)
=
∞
∑
j=0
(j+1)( C(i－1,j) － C(i－1,j－1) )Xj
=
∂
∂X
lb36
∞
∑
j=0
C(i－1,j)Xj+1
rb36 －
∂
∂X
lb36
∞
∑
j=0
C(i－1,j+1)Xj+1
rb36
=
∂
∂X
( (X－1)pi－1(X) )
が成り立ちます。qi(X)=(X－1)pi(X)とおくと
qi(X) = (X－1)
∂
∂X
qi－1(X), i≧1
ですから
qi(X) = 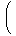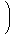lb36
(X－1)
∂
∂X
rb36
i
q0(X)
となります。命題4.6.34を適用して、Xに0を代入すると
qi(0)
=
i
∑
j=0
{i
j		}
(－1)jqi(j)(0)
=
i
∑
j=0
{i
j		}
(－1)jj!( C(0,j－1) － C(0,j) )
=
i－1
∑
j=0
{i
j+1		}
(－1)j+1(j+1)!C(0,j)
 －
i
∑
j=0
{i
j		}
{(－1)jj!C(0,j)}
=
－
i
∑
j=0
(－1)jj!C(0,j)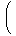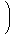lb36
(j+1)
{i
j+1		}
 + 
{i
j		}
rb36
=
－
i
∑
j=0
(－1)jj!
{i+1
j+1		}
C(0,j)
となり、
pi(0) =
i
∑
j=0
(－1)jj!
{i+1
j+1		}
C(0,j)
が得られました。これにより、
C(0,j) =
1
j+1
, j≧0
として、最初の生成規則を適用すればベルヌーイ数の計算公式IIから三角形算術でベルヌーイ数が求められることがわかりました。
 この方法でベルヌーイ数を計算してみます。

sample4.6.6.py

from Poly1 import *
 
C = []; Input = []; Output = []
for i in range( 9 ):
  C.append( Fraction(1,i+1) )
for i in range( 9 ):
  Input.append( Poly1( [C[i]] ) )
print Input
for i in range( 9 ):
  for j in range( 8, i, -1 ):
    C[j] = (j - i) * ( C[j-1] - C[j] )
for i in range( 9 ):
  Output.append( Poly1( [C[i]] ) )
print Output

sample4.6.6.pyの実行結果

[1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9]
[1, 1/2, 1/6, 0, -1/30, 0, 1/42, 0, -1/30]

sample4.6.6.rb

require 'mathn'
require './poly1'
 
C = []; Input = []; Output = []
for i in 0...9
  C.push(1/(i+1))
end
for i in 0...9
  Input.push(Poly1([C[i]]))
end
p Input
for i in 0...9
  for j in ((i+1)..8).to_a.reverse
    C[j] = (j - i) * ( C[j-1] - C[j] )
  end
end
for i in 0...9
  Output.push(Poly1([C[i]]))
end
p Output

sample4.6.6.rbの実行結果

[1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9]
[1, 1/2, 1/6, 0, -1/30, 0, 1/42, 0, -1/30]

参考文献

[1] グレアム, クヌース, パタシェニク, コンピュータの数学, 共立出版, 1993
img
 
 
[2] 荒川恒男, 金子昌信, 伊吹山知義, ベルヌーイ数とゼータ関数, 牧野書店, 2001
img
 
 
人　　物
アイザック・ニュートン Newton, Isac, 1642-1727
イギリスの物理学者・数学者・天文学者。古典力学(ニュートン力学)の創始し、ライプニッツとは独立して微積分法を創り上げる。
 
数　　学
線形空間 せんけいくうかん, linear space
ベクトル空間 べくとるくうかん, vector space
ベクトル べくとる, vector
スカラー すからー, scalar
線形結合 せんけいけつごう, linear combination
線形従属 せんけいじゅうぞく, linearly dependent
線形独立 せんけいどくりつ, linearly independent
部分空間 ぶぶんくうかん, subspace
基底 きてい, basis
次元 じげん, dimension
差分 さぶん, difference
n階差分 nかいさぶん, difference of n-th order
線形写像 せんけいしゃぞう, linear mapping
線形作用素 せんけいさようそ, linear operator
和分 わぶん, summation
ニュートン級数 にゅーとんきゅうすう, Newton series
 
Published by SANENSYA Co.,Ltd.