一次不定方程式
著者:梅谷 武
語句:オイラー,アールヤバタ,不定方程式
一次不定方程式のユークリッドの互除法を使った解法について述べる。
作成:2006-04-25
更新:2021-03-17
aで割れば
r1余り、
bで割れば
r2余るような整数
nを求めよ。
という問題があります。これを
| n = ax + r1 = by + r2, 0≦r1<a, 0≦r2<b
|
と表し、
r2 - r1 = cとおくと2元一次不定方程式
となりますが、アールヤバタはこれを割り算で
a,bを小さい数に還元して解いています。小さい数に還元するというのは
a>b>0と仮定して
a = bq + r, 0≦r<bなる
q,rを求め、
aに代入し
というように
aを
bより小さい数
rに置き換えることです。アールヤバタは簡単に解けるぐらいに係数が小さくなった時点で打ち切っていましたが、これを繰り返すといつかは
r=0となり、
dx'=c, d=gcd(a,b)という一元一次不定方程式に還元され、
d|cの場合に解けることがわかります。この節ではこのように一次不定方程式をユークリッドの互除法を使って解くことについて考えます。
整数
ai, i=1,⋯,nが生成するイデアル
(a1, ⋯, an)は
| { a1 x1 + ⋯ + an xn | xi∈ℤ }
|
という集合でした。この節ではこの集合の元の形式における
xiを
n個の変数として、ある整数
cに対する
という方程式の整数解について考えます。一般に代数方程式の整数解を求めるときに、その方程式を
不定方程式ふていほうていしき, indeterminate equationといいます。上の式のように方程式が変数の一次式であるときに一次不定方程式といいます。
{ a1 x1 + ⋯ + an xn | xi∈ℤ } ∩ ℕの最小元を
dとすると
| (d) = { a1 x1 + ⋯ + an xn | xi∈ℤ }
|
となることがわかっていますから、この不定方程式の解が存在することと
c∈(d)、すなわち
cが
dの倍数であることは同じことです。まず、
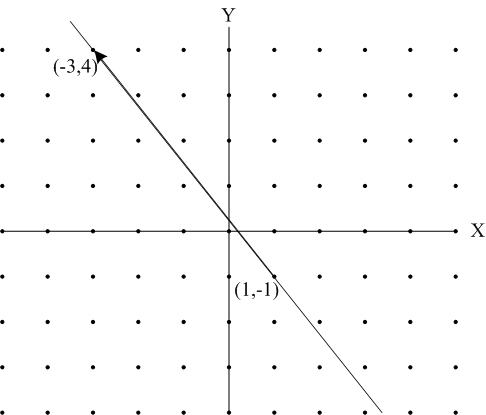
c=dのときを考えましょう。2変数の場合を具体例でみてみます。
| 15X + 12Y = 3, 3 = gcd(15,12)
|
とします。これはX-Y平面上の直線の方程式と考えることができます。この直線をパラメータ表示してみましょう。
から
となりますが、この整数解はちょうど
tを整数としたときに得られることがわかります。これを一般化して命題の形にまとめておきましょう。
0でない整数
a,bに関する一次不定方程式
| aX + bY = d, d = gcd(a,b), a=a'd, b=b'd
|
は無限個の解をもち、その一般解は一つの特殊解を
(x0,y0)としたときに
| { (x0 - b't, y0 + a't) | t∈ℤ } |
と書くことができる。
証明
一般解を(x,y)とするとa'(x-x0)=-b'(y-y0)となり(a',b')=1よりx-x0=-b't, y-y0=a't, t∈ℤと書ける。■
上の命題における特殊解はユークリッドの互除法を少し拡張することで最大公約数と同時に計算することができます。互除法とは、
0でない整数
a,bが与えられたときに、
という数列
(ai),(bi),(qi),(ri)を
rn=0となるまで計算するものでした。これを次のように書き直します。すなわち、
0でない整数
a,b(a>b)が与えられたときに、
x0 = a, x1 = bとし、
| | |
| | |
| | |
| | | ki-1 xi + xi+1, 0<xi+1<|xi| |
|
| | |
| | |
という数列
(xi),(ki)を
xn+2=0となるまで計算するものと考えます。ここで数列
(xi)は狭義の単調減少数列になっているので必ず有限回で止まります。これを行列で表現してみましょう。
xi,xi+1から
xi+1,xi+2を計算する部分は次のように書くことができます。
したがって
となりますから、行列
を計算していけば
d=un a + wn bとなり、特殊解
(un, wn)が得られます。しかし行列の計算を行うと計算量が多くなりますので、工夫して計算量を減らします。クヌースによれば以下のアイディアはGordon H. Bradleyによるものです。
であることから
dと
unだけを求めるようにしてみましょう。
において、
unが
un-1,vn-1にしか依存していないことに注目すると、数列
(ui),(vi)だけを計算していけば最終的に
unが得られることがわかります。これを算法として整理し、そのままプログラミングしてみます。
0でない二つの整数
a,bの最大公約数
dと
ax+by=dなる
x,yを求める。
| Step 1.
| s = a; t = b; u = 1; v = 0 |
| Step 2.
| s = tq + r, 0≦r<|b|となるq,rを求める。
|
| Step 3.
| もしr = 0であればStep.5へ。
|
| Step 4.
| s = t; t = r; temp = v; u = u - q*v; u = temp |
| Step 5.
| d = s; x = u; y = ( s - u * a ) / b |
def gcd_ext( a, b, val = [ 0, 0 ] ):
if ( a == 0 ) or ( b == 0 ):
return 0
s = a; t = b; u = 1; v = 0
while t != 0:
q = s / t; r = s % t
s = t; t = r
temp = v; v = u - q * v; u = temp
val[0] = u
val[1] = ( s - u * a ) / b
if s < 0:
val[0] = -val[0]
val[1] = -val[1]
return -s
else:
return s
a = 9749560641517; b = 8770036831691
val = [ 0, 0 ]
d = gcd_ext( a, b, val )
x = val[0]; y = val[1]
print 'gcd( %d, %d ) = %d' % ( a, b, d )
print 'a*(%d) + b*(%d) = %d' % ( x, y, (a*x + b*y) )
gcd( 9749560641517, 8770036831691 ) = 6972593
a*(251903) + b*(-280038) = 6972593
def gcd_ext(a, b, val = [0, 0])
if ( a == 0 ) or ( b == 0 )
return 0
end
s = a; t = b; u = 1; v = 0
while t != 0
q = s / t; r = s % t
s = t; t = r
temp = v; v = u - q * v; u = temp
end
val[0] = u
val[1] = (s - u * a) / b
if s < 0
val[0] = -val[0]
val[1] = -val[1]
return -s
else
return s
end
end
a = 9749560641517; b = 8770036831691; val = [0, 0]
d = gcd_ext(a, b, val)
x = val[0]; y = val[1]
printf "gcd(%d, %d) = %d\n", a, b, d
printf "a*(%d) + b*(%d) = %d\n", x, y, (a*x + b*y)
gcd(9749560641517, 8770036831691) = 6972593
a*(251903) + b*(-280038) = 6972593
ここまでで2元一次不定方程式
aX+bY=d, d=gcd(a,b)を解くことができました。次に任意の整数
cに対する
aX+bY=cの解法について考えます。
cが
dの倍数でなければ解は存在しませんから、
c=c'dと仮定します。
図2.6.6の例で考えましょう。
| 15X + 12Y = 2・3, 3 = gcd(15,12)
|
とすると、この直線のパラメータ表示は元のパラメータ表示で始点ベクトルをちょうど
2倍することで得られます。
この整数解は
tを整数としたときに得られます。これを一般化して命題の形にまとめます。
0でない整数
a,bに関する一次不定方程式
| aX + bY = c, d = gcd(a,b), a=a'd, b=b'd, c=c'd
|
は無限個の解をもち、その一般解は
aX + bY = dの一つの特殊解を
(x0,y0)としたときに
| { (c'x0 - b't, c'y0 + a't) | t∈ℤ }
|
と書くことができる。
証明
演習とする。■
さて、一般の
n元一次不定方程式
a1x1 + ⋯ + anxn =cの解法ですが、線形代数の立場から見ると方程式が
n次元ユークリッド空間
ℝnの超平面の方程式
<`a,`x>=cの形をしていることから、この超平面上の整数の格子点を求めることと同じです。ここでは
n=3の場合だけを考えることにします。
| a1 X1 + a2 X2 + a3 X3 = d, d = gcd(a1,a2,a3)
|
とし、この特殊解
(x1,x2,x3)が与えられたとしましょう。
a1(X1-x1)+a2(X2-x2)+a3(X3-x3)=0から
| a3 ( X3 - x3 ) = - ( a1 ( X1 - x1 ) + a2 ( X2 - x2 ) )
|
ここで
a3 = a3'd, a1 = a1'd'd, a2 = a2'd'd, d'=gcd(a1,a2)とすると、
| a3' ( X3 - x3 ) = -d'( a1' ( X1 - x1 ) + a2' ( X2 - x2 ) )
|
より
d'|( X3 - x3 )ですから、
と書くことができます。これを代入して、
| a3' u = - ( a1' ( X1 - x1 ) + a2' ( X2 - x2 ) )
|
とおくと
| a1' X1' + a2' X2' = - a3'u, u ∈ ℤ
|
となります。この一般解は
a1' X1' + a2' X2' = 1の一般解に
- a3'uを掛けたものになりますのでこの特殊解を
(s1,s2)とすると、
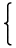 | | | , t,u ∈ ℤ
|
ここまでの結果を整理すると求める一般解
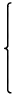 | | | , t,u ∈ ℤ
|
が得られます。この一般解が実際に求める方程式の解になっていること、つまり整数で
3次元空間内の平面
a1 X + a2 Y + a3 Z = d上にあることは容易に確かめることができます。これを命題の形にまとめます。
0でない整数
a,b,cに関する一次不定方程式
| a1 X1 + a2 X2 + a3 X3 = d, d = gcd(a1,a2,a3)
|
は無限個の解をもち、その一般解は特殊解を
(x1,x2,x3)とし、
| a3 = a3'd, a1 = a1'd'd, a2 = a2'd'd, d'=gcd(a1,a2)
|
とおいたときの
a1' X + a2' Y = 1の特殊解を
(s1,s2)としたとき、次のように書くことができる。
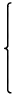 | | | , t,u ∈ ℤ
|
この命題から3元一次不定方程式の解法はその特殊解を求めることに帰着されます。これはイデアルとして
(a1, a2, a3) = ((a1, a2), a3)となることから
d'=gcd(a1, a2)とおくと
d = gcd(a1, a2, a3) = gcd(d', a3)となり、
の特殊解を
(x0, y0)とし、
の特殊解を
(u0, z0)とすれば、
(x0 u0, y0 u0, z0)が求める特殊解となり、拡張互除法を2回適用することで計算できます。この方法をプログラミングしてみましょう。
def gcd_ext( a, b, val = [ 0, 0 ] ):
if ( a == 0 ) or ( b == 0 ):
return 0
s = a; t = b; u = 1; v = 0
while t != 0:
q = s / t; r = s % t
s = t; t = r
temp = v; v = u - q * v; u = temp
val[0] = u
val[1] = ( s - u * a ) / b
if s < 0:
val[0] = -val[0]
val[1] = -val[1]
return -s
else:
return s
def gcd_ext3( a1, a2, a3, val = [ 0, 0, 0 ] ):
val1 = [ 0, 0 ]; val2 = [ 0, 0 ]
d1 = gcd_ext( a1, a2, val1 )
d = gcd_ext( d1, a3, val2 )
val[0] = val1[0]*val2[0]
val[1] = val1[1]*val2[0]
val[2] = val2[1]
return d
a = 2418976464533; b = 2587070861497
c = 69314547013;
val = [ 0, 0, 0 ]
d = gcd_ext3( a, b, c, val )
x = val[0]; y = val[1]; z = val[2]
print 'gcd( %d, %d, %d ) = %d' % ( a, b, c, d )
print 'a*(%d) + b*(%d) + c*(%d) = %d' % ( x, y, z, (a*x + b*y + c*z) )
gcd( 2418976464533, 2587070861497, 69314547013 ) = 9941
a*(4809212484) + b*(-4496734855) + c*(-1392) = 9941
def gcd_ext(a, b, val = [0, 0])
if ( a == 0 ) or ( b == 0 )
return 0
end
s = a; t = b; u = 1; v = 0
while t != 0
q = s / t; r = s % t
s = t; t = r
temp = v; v = u - q * v; u = temp
end
val[0] = u
val[1] = (s - u * a) / b
if s < 0
val[0] = -val[0]
val[1] = -val[1]
return -s
else
return s
end
end
def gcd_ext3(a1, a2, a3, val = [0, 0, 0])
val1 = [0, 0]; val2 = [0, 0]
d1 = gcd_ext(a1, a2, val1)
d = gcd_ext(d1, a3, val2)
val[0] = val1[0]*val2[0]
val[1] = val1[1]*val2[0]
val[2] = val2[1]
return d
end
a = 2418976464533; b = 2587070861497; c = 69314547013
val = [0, 0, 0]
d = gcd_ext3(a, b, c, val)
x = val[0]; y = val[1]; z = val[2]
printf "gcd(%d, %d, %d) = %d\n", a, b, c, d
printf "a*(%d) + b*(%d) + c*(%d) = %d\n",
x, y, z, (a*x + b*y + c*z)
gcd(2418976464533, 2587070861497, 69314547013) = 9941
a*(4809212484) + b*(-4496734855) + c*(-1392) = 9941
一般のn元一次不定方程式の特殊解は同じように拡張ユークリッド算法をn-1回適用することで求めることができます。一般解の構造については連立一次不定方程式の解法とともに線形代数を使って説明するのが適切ですので、ここでは詳細を述べないことにします。
[
2] 木田 祐司, 牧野 潔夫, UBASICによるコンピュータ整数論, 日本評論社, 1994
人 物
オイラー Euler, Leonhard, 1707-1783
スイスの数学者。ライプニッツの形式的代数計算を継承、発展させ数学史上最大級の業績を残す。その全集の刊行は21世紀となった現代においてもまだ完結していない。
アールヤバタ Ārayabhata, 476-?
インドの天文学者、数学者。
数 学
不定方程式 ふていほうていしき, indeterminate equation