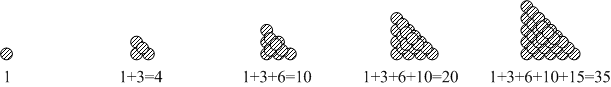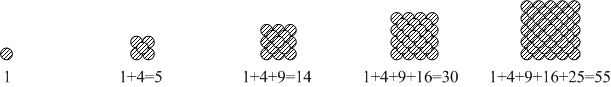立体数
著者:梅谷 武
語句:四面体数,三角錐数,四角錐数,九九,グノーモン
立体数と∑記法。
作成:2006-04-20
更新:2013-06-14
1.8 立体数
 同じ大きさの球で三角数を作り、それを順番に積み上げていくと四面体ができます。この四面体の球の個数は三角数を順番に加えていった数になっています。このように第n項が三角数の和Δ1+Δ2+ ⋯ + Δnで表されるような数を四面体数しめんたいすう, tetrahedral numberあるいは三角錐数さんかくすいすう, triangular pyramidal numberといいます。
図1.8.2 四面体数
四面体数
n番目の四面体数をTetnで表すと
Tetn =
1
2
(1×2 + 2×3 + ⋯ + n(n+1))
となりますが、これは連続数の積の和の半分になっています。ここで数式を見易くするために数列の和を表す記号∑を導入し、
n
∑
k=1
k(k+1)
 = 1×2 + 2×3 + ⋯ + n(n+1)
と書くことにしましょう。k(k+1)(k+2) － (k－1)k(k+2) = 3k(k+1)から、
3
n
∑
k=1
k(k+1)
=
n
∑
k=1
( k(k+1)(k+2) － (k－1)k(k+1) )
=
n(n+1)(n+2) － 0×1×2 = n(n+1)(n+2)
となり、連続する二つの数の和の公式：
(1.1)
n
∑
k=1
k(k+1)
 =
n(n+1)(n+2)
3
が得られます。これより四面体数は次のように表すことができます。
(1.2)
Tetn =
n
∑
k=1
Δk
 =
n(n+1)(n+2)
6
 同じ大きさの球で四角数を作り、それを順番に積み上げていくと四角錐ができます。この四角錐の球の個数は四角数を順番に加えていった数になっています。このように第n項が四角数すなわち平方数の和12+22+ ⋯ + n2で表されるような数を四角錐数しかくすいすう, square pyramidal numberといいます。
図1.8.5 四角錐数
四角錐数
n番目の四角錐数をPyrnで表すことにしましょう。これは三角数と平方数との関係Δn + Δn－1 = n2を使うと
Pyrn
=
Tetn + Tetn－1
=
n(n+1)(n+2)
6
 +
(n－1)n(n+1)
6
=
n(n+1)(2n+1)
6
となり、四角錐数は次のように表すことができます。
(1.3)
Pyrn =
n
∑
k=1
k2
 =
n(n+1)(2n+1)
6
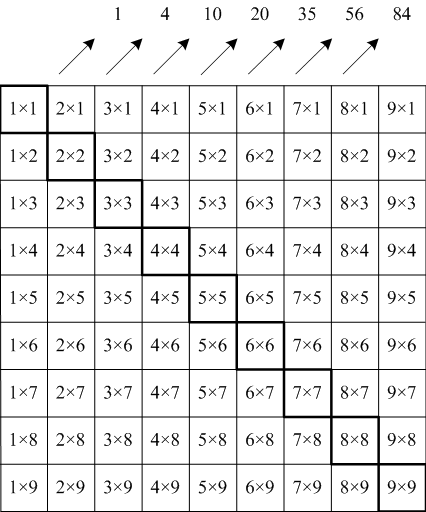
 我々は小学生のときに掛け算の九九くく, 9×9 multiplication tableというものを暗記させられました。そのときに九九表というものを使いますが、これは一般に乗算表と呼ばれるものの一部になっています。
図1.8.8 乗算表と平方数及び四面体数
乗算表と平方数及び四面体数
この乗算表にはさまざまな数が並んでいます。すぐにわかるのが左上から右下の対角線に平方数が並んでいることです。それから左下から右上に向かう対角線の和を求めると
1
=
1×1
4
=
1×2 + 2×1
10
=
1×3 + 2×2 + 3×1
20
=
1×4 + 2×3 + 3×2 + 4×1
⋮
という数列になりますが、これは次のように考えると四面体数と一致していることがわかります。
Tetn
=
1 +
1 + 2 +
1 + 2 + 3 +
⋮
1 + 2 + 3 + ⋯ + n
=
1×n + 2×(n－1) + 3×(n－2) + ⋯ + n×1
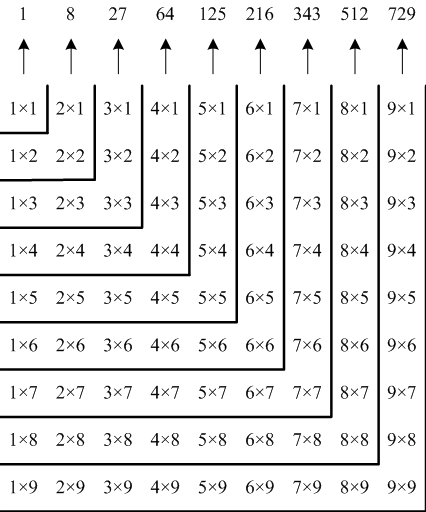
 次に乗算表をグノーモンぐのーもん, gnomonと呼ばれるL字型の領域に分割してその和を求めてみましょう。
図1.8.11 乗算表と立方数
乗算表と立方数
このようにn番目がnの３乗である数列を立方数といいます。上の図はn×nの乗算表の数の総和がn番目までの立方数の総和に等しいことを示しています。n×nの乗算表の数の総和は、
(1+2+⋯+n)(1+2+⋯+n) = (Δn)2
ですから、立方数の和は
(1.4)
n
∑
k=1
k3
 = (Δn)2 =
n2(n+1)2
4
となることがわかりました。
数　　学
四面体数 しめんたいすう, tetrahedral number
三角錐数 さんかくすいすう, triangular pyramidal number
四角錐数 しかくすいすう, square pyramidal number
九九 くく, 9×9 multiplication table
インドでは22×20までの乗算表を暗記する。
グノーモン ぐのーもん, gnomon
古代ギリシア語で日時計の針という意味。ピュタゴラス派の数論の用語として使われた。
 
Published by SANENSYA Co.,Ltd.