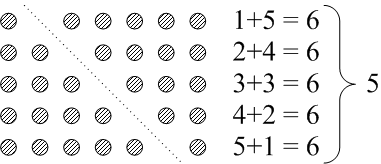
まず1から5までの和を求めてみることにしましょう。図のように1個から5個までの小石を三角に並べて、それを二つ合わせて長方形を作ります。この長方形の小石の数を横方向の行の長さ6で計ると5になります。6×5=30ですから、求める和はこれを2で割った15となります。これと同じように考えれば、1から100までの和は101×100=10100を2で割って5050と求めることができます。

 小石が三角形に並んでいることからこの数は三角数さんかくすう, trianglar numberと呼ばれています。n番目の三角数をΔ_nあるいはΔ(n)と書くことにします。この計算法は1からどんな自然数nまでの和についても同じように使うことができますから次のような公式が得られます。

 2で割り切れる数を偶数ぐうすう, even numberといい、2で割り切れない数を奇数きすう, odd numberといいます。数を小さい順に並べると偶数と奇数が交互に表れます。

      0   2   4   6   8 　 …　偶数
        1   3   5   7   9　 …　奇数

 まず2から10までの偶数の和を求めてみることにしましょう。偶数は2で割り切れるので例題1.6.1の解法で最後に2で割ることを省略すれば結果が出てきます。 このやり方を使うと例題は次のように計算することができます。 これは前の公式を二倍した次のような公式を使っていることになります。

 すぐに気が付くように例題1.6.1の答え5050から例題1.6.2の答え2550を引けば答え2500が出てきます。これを任意の数nに拡張してみます。 これにより次の公式が求まりました。

 等しい数を二つ掛けた数を平方数へいほうすう, square numberといいます。上の公式は平方数が奇数列の和で表されることを示しています。

図においてΔ₅+Δ₆=6²が成り立つことが示されていますが、このように連続する三角数を加えると平方数になります。

 同じようにして一般の等差数列とうさすうれつ, arithmetic sequenceの和も求めることができます。初項しょこう, first termがa、公差こうさ, common differenceがdの等差数列を考えましょう。第n項はa_n = a + (n－1)dで表すことができます。 これを反対に並べます。 これらの二つの和を求めます。 このことから等差数列の和の公式を導くことができました。