整数
著者:梅谷 武
語句:自然数,整数,正,負,加法群,可換群,アーベル群,加群,可換環,零因子,整域,順序,順序環
整数の定義と性質。
作成:2006-04-11
更新:2021-03-15
前節で定義した数を
自然数しぜんすう, natural numberと呼び、自然数全体の集合を
ℕで表わすことにします。
整数せいすう, integerとは、
0でない自然数の集合を
正せい, positiveの数
とし、
を
負ふ, negativeの数として
と定義される集合です。自然数は物の個数として定義されましたが、減算を定義しようとすると大きい数から小さい数を引くことしかできませんでした。整数における負の数は小さい数から大きい数を引くときの不足している数という意味を持ちます。小さい数にこの不足している数を足すことによって大きい数をちょうど引くことができるようになります。この節では整数の基本的な性質を列挙します。これらの性質が整数に関する議論の出発点となります。
整数の加法に関する性質は加法群という概念で表現することができます。
集合
Gの2つの元
a, bについて加法
a + b ∈ Gが定義されていて
次の性質を満たすとき、
Gは
加法群かほうぐん, additive groupであるという。
| (結合律)
| 任意の3元a, b, cについて、(a + b) + c = a + (b + c) |
| (零元)
| 0∈Rが存在し、任意の元aについて、a + 0 = 0 + a = a |
| (逆元)
| 任意の元aについて-aが存在して、a + (-a) = (-a) + a = 0 |
| (可換律)
| 任意の2元a, bについて、a + b = b + a |
負の数に対する加法は自然に導入することができますが、乗法については次のような約束をすることにします。任意の整数
aについて
-a = -1 × aと定め、
-1に関する積を
と定めます。これにより任意の整数に対する積が計算できます。このように加法と乗法を定めることにより整数は次のような可換環の性質をもつようになりました。
集合
Rの2つの元
a, bについて加法
a + b ∈ Rと乗法
ab ∈ Rが定義されていて次の性質を満たすとき、
Rは
可換環かかんぐん, commutative ringであるという。
(R1)
Rは加法に関して加法群を為す。すなわち、次が成り立つ。
| (結合律)
| 任意の3元a, b, cについて、(a + b) + c = a + (b + c) |
| (零元)
| 0∈Rが存在し、任意の元aについて、a + 0 = 0 + a = a |
| (逆元)
| 任意の元aについて-aが存在して、a + (-a) = (-a) + a = 0 |
| (可換律)
| 任意の2元a, bについて、a + b = b + a |
(R2)
Rの乗法について次が成り立つ。
| (結合律)
| 任意の3元a, b, cについて、(ab)c = a(bc) |
| (単位元)
| 1∈Rが存在し、任意の元aについて、a1 = 1a = a |
| (可換律)
| 任意の2元a, bについて、ab = ba |
(R3)
Rの加法と乗法について次が成り立つ。
1と-1以外の数は乗法に関する逆元を持ちませんので乗法群にはなりません。
整数は整域です。整数における順序は減算によって定めますが、一般に順序とは次のようなものとして定義されます。
整数の任意の2元の関係a ≦ bをb - aが0か正であることと定義します。そうするとこの関係は順序となります。a ≦ bはb ≧ aとも書き、a ≦ bであり、かつa ≠ bのときa < bあるいはb > aと書きます。これにより整数は次のような順序環としての性質をもちます。
可換環
Rに順序が定義され、その順序が次の性質をもつとき
順序環じゅんじょかん, ordered ringという。
| (O1)
| 任意のx,y∈Rに対し、x < y, x = y, x > yのいずれかが成り立つ。
|
| (O2)
| x < y, y < z ⇒ x < z |
| (O3)
| x < y, z > 0 ⇒ xz < yz |
| (O4)
| x < y ⇒ x + z < y + z |
順序環に対して次のように絶対値を定義することができます。
| |x| ≔ | 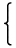 | | |
|
Rを順序環とすると次が成り立つ。
| (O5)
| 任意の元xに対し、|x|≧0であり|x|=0となるのはx=0のときに限る。
|
| (O6)
| |xy| = |x||y| |
| (O7)
| |x+y| ≦ |x|+|y| |
証明
(O5)は絶対値が定義から正か0にしかならないことからわかる。(O6)はx,yそれぞれが正・0・負の場合に分けて考えればよい。(O7)はまず
|x| ≧ x, |y| ≧ yより、(O4)を使って
また
|x| ≧ -x, |y| ≧ -yより
であり、
|x + y|は
x + yか
-(x + y)のいずれかであることから(O7)が成り立つことがわかる。■
これらの性質から順序環は整域になることがわかります。
整数の基本的な性質は次の命題で表現することができます。
ここではこの命題を証明無しで認めることにします。これを証明する体系的な議論に興味がある方は文献[1],[2],[3]等を参照してください。
数 学
自然数 しぜんすう, natural number
整数 せいすう, integer
正 せい, positive
負 ふ, negative
加法群 かほうぐん, additive group
可換群 かかんぐん, commutative group
アーベル群 あーべるぐん, abelian group
アーベル(N.H.Abel, 1802-1829)の代数方程式のガロア群が可換であればその方程式は可解であるという業績にちなんで名付けられた。
加群 かぐん, module
可換環 かかんぐん, commutative ring
零因子 れいいんし, zero divisor
整域 せいいき, integral domain
順序 じゅんじょ, order
順序環 じゅんじょかん, ordered ring


