2.3 正多面体
著者:梅谷 武
語句:正四面体と立方体の対称変換群、正八面体と立方体、正十二面体と正二十面体の双対性を視覚的に示す。
語句:正四面体と立方体の対称変換群、正八面体と立方体、正十二面体と正二十面体の双対性を視覚的に示す。
対称変換群, 対称群, 正四面体, 立方体, 正八面体, 正十二面体, 正二十面体
作成:2010-09-30
更新:2011-03-08
更新:2011-03-08
正多面体の対称変換群たいしょうへんかんぐん, symmetry transformation groupは直交群の有限部分群であり、対称群たいしょうぐん, symmetric groupに埋め込むことができる。ここでは五種類の正多面体の内、正四面体と立方体の対称変換群の構造とともに、正八面体と立方体、正十二面体と正二十面体の双対性を視覚的に示す。
正四面体せいしめんたい, regular tetrahedronの対称変換で回転で表現できるものは、重心と頂点を結ぶ4本の軸に関する回転と二組の頂点対に関する互換の積であり、位数12の群を成し、交代群A4と同型になる。そのすべてを図示する。
sample214.lua
package.path = "std/?.lua"
require( "Geometry" )
a = math.sqrt( 6.0 ) / 2.0
b = math.sqrt( 3.0 ) / 3.0
c = math.sqrt( 6.0 ) / 6.0
d = 2.0 * b
vertices = {
0.0, a, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0,
-1.0, -c, -b, 0.0, 1.0, 0.0, 0.0, 0.0,
1.0, -c, -b, 0.0, 1.0, 0.0, 0.0, 0.0,
0.0, -c, d, 0.0, 1.0, 0.0, 0.0, 0.0
}
function tetrahedron()
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
dxSetColorHSV( 0.0, 1.0, 1.0 )
dxTriangleMesh( 4, vertices, 1, { 0, 1, 2 } )
dxSetColorHSV( 90.0, 1.0, 1.0 )
dxTriangleMesh( 4, vertices, 1, { 0, 2, 3 } )
dxSetColorHSV( 180.0, 1.0, 1.0 )
dxTriangleMesh( 4, vertices, 1, { 0, 3, 1 } )
dxSetColorHSV( 270.0, 1.0, 1.0 )
dxTriangleMesh( 4, vertices, 1, { 1, 3, 2 } )
dxPrint( 0.0+0.1, a+0.1, 0.0+0.1, 1.0, 1.0, 1.0, "1" )
dxPrint(-1.0-0.1, -c-0.1, -b-0.1, 1.0, 1.0, 1.0, "2" )
dxPrint( 1.0+0.1, -c-0.1, -b-0.1, 1.0, 1.0, 1.0, "3" )
dxPrint( 0.0+0.1, -c-0.1, d+0.1, 1.0, 1.0, 1.0, "4" )
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
Tetrahedron = Figure.new( function()
tetrahedron()
end )
E = Transformation.new( function()
end )
R1 = Transformation.new( function()
Rotate( 120.0, 0.0, 0.0, 1.0 )
end )
R2 = Transformation.new( function()
Rotate( 120.0, -1.0, -b, -c )
end )
R3 = Transformation.new( function()
Rotate( 120.0, 1.0, -b, -c )
end )
R4 = Transformation.new( function()
Rotate( 120.0, 0.0, d, -c )
end )
T1 = Transformation.new( function()
Translate( 3.0, 0.0, 0.0 )
end )
T2 = Transformation.new( function()
Translate( 0.0,-3.0, 0.0 )
end )
draw = E * Tetrahedron
draw = ( T1 * R1 ) * Tetrahedron
draw = ( T1^2 * R1^2 ) * Tetrahedron
draw = ( T1 * T2 * R2 ) * Tetrahedron
draw = ( T1^2 * T2 * R2^2 ) * Tetrahedron
draw = ( T1 * T2^2 * R3 ) * Tetrahedron
draw = ( T1^2 * T2^2 * R3^2 ) * Tetrahedron
draw = ( T1 * T2^3 * R4 ) * Tetrahedron
draw = ( T1^2 * T2^3 * R4^2 ) * Tetrahedron
draw = ( T1^4 * R2^2 * R1 ) * Tetrahedron
draw = ( T1^4 * T2 * R4^2 * R2 ) * Tetrahedron
draw = ( T1^4 * T2^2 * R2^2 * R3 ) * Tetrahedron
tnNewObject()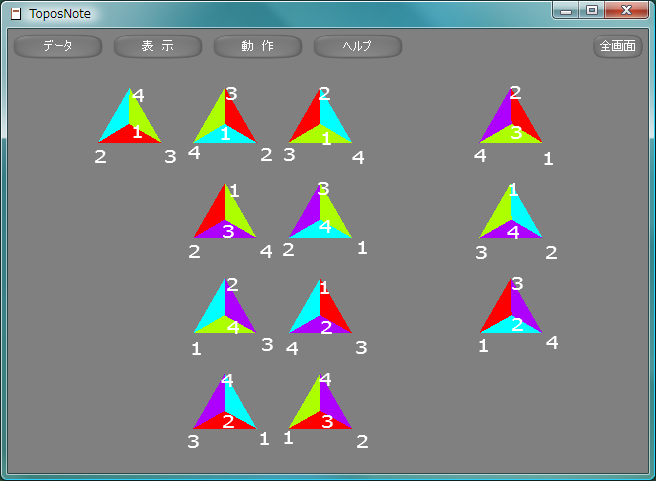
立方体りっぽうたい, cubeの対称変換で回転で表現できるものは、4本の対角線の置換として表現することができ、そのすべての組み合わせに対応する回転が存在することから、対称群S4に同型であることがわかる。そのすべてを図示する。
sample215a.lua
package.path = "std/?.lua"
require( "Geometry" )
a = math.sqrt( 3.0 ) / 3.0
vertices = {
-a, -a, -a, -a, -a, -a, 0.0, 0.0,
-a, -a, a, -a, -a, a, 0.0, 0.0,
a, -a, a, a, -a, a, 0.0, 0.0,
a, -a, -a, a, -a, -a, 0.0, 0.0,
-a, a, -a, -a, a, -a, 0.0, 0.0,
-a, a, a, -a, a, a, 0.0, 0.0,
a, a, a, a, a, a, 0.0, 0.0,
a, a, -a, a, a, -a, 0.0, 0.0
}
function cube()
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
dxSetColorHSV( 0.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 0, 1, 2, 0, 2, 3 } )
dxSetColorHSV( 60.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 1, 5, 6, 1, 6, 2 } )
dxSetColorHSV( 120.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 5, 4, 7, 5, 7, 6 } )
dxSetColorHSV( 180.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 4, 0, 3, 4, 3, 7 } )
dxSetColorHSV( 240.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 0, 4, 5, 0, 5, 1 } )
dxSetColorHSV( 300.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 2, 6, 7, 2, 7, 3 } )
dxPrint( -a-0.1, -a-0.1, -a-0.1, 1.0, 1.0, 1.0, "1" )
dxPrint( -a-0.1, -a-0.1, a+0.1, 1.0, 1.0, 1.0, "2" )
dxPrint( a+0.1, -a-0.1, a+0.1, 1.0, 1.0, 1.0, "3" )
dxPrint( a+0.1, -a-0.1, -a-0.1, 1.0, 1.0, 1.0, "4" )
dxPrint( -a-0.1, a+0.1, -a-0.1, 1.0, 1.0, 1.0, "5" )
dxPrint( -a-0.1, a+0.1, a+0.1, 1.0, 1.0, 1.0, "6" )
dxPrint( a+0.1, a+0.1, a+0.1, 1.0, 1.0, 1.0, "7" )
dxPrint( a+0.1, a+0.1, -a-0.1, 1.0, 1.0, 1.0, "8" )
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
Cube = Figure.new( function()
cube()
end )
E = Transformation.new( function()
end )
R1 = Transformation.new( function()
Rotate( 90.0, 1.0, 0.0, 0.0 )
end )
R2 = Transformation.new( function()
Rotate( 90.0, 0.0, 1.0, 0.0 )
end )
R3 = Transformation.new( function()
Rotate( 90.0, 0.0, 0.0, 1.0 )
end )
T1 = Transformation.new( function()
Translate( 2.0,-2.0, 0.0 )
end )
T2 = Transformation.new( function()
Translate(-2.0,-2.0, 0.0 )
end )
draw = E * Cube
draw = ( T1 * R1 ) * Cube
draw = ( T1^2 * R1^2 ) * Cube
draw = ( T1^3 * R1^3 ) * Cube
draw = ( T1 * T2 * R2 ) * Cube
draw = ( T1^2 * T2 * R2^2 ) * Cube
draw = ( T1^3 * T2 * R2^3 ) * Cube
draw = ( T1 * T2^2 * R3 ) * Cube
draw = ( T1^2 * T2^2 * R3^2 ) * Cube
draw = ( T1^3 * T2^2 * R3^3 ) * Cube
tnNewObject()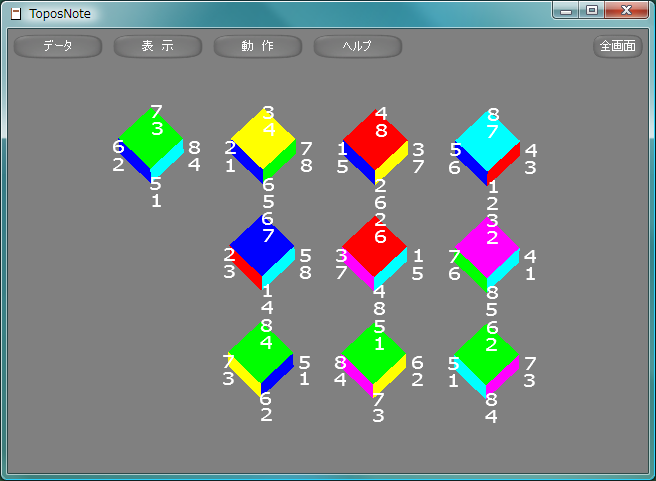
sample215b.lua
package.path = "std/?.lua"
require( "Geometry" )
a = math.sqrt( 3.0 ) / 3.0
vertices = {
-a, -a, -a, -a, -a, -a, 0.0, 0.0,
-a, -a, a, -a, -a, a, 0.0, 0.0,
a, -a, a, a, -a, a, 0.0, 0.0,
a, -a, -a, a, -a, -a, 0.0, 0.0,
-a, a, -a, -a, a, -a, 0.0, 0.0,
-a, a, a, -a, a, a, 0.0, 0.0,
a, a, a, a, a, a, 0.0, 0.0,
a, a, -a, a, a, -a, 0.0, 0.0
}
function cube()
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
dxSetColorHSV( 0.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 0, 1, 2, 0, 2, 3 } )
dxSetColorHSV( 60.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 1, 5, 6, 1, 6, 2 } )
dxSetColorHSV( 120.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 5, 4, 7, 5, 7, 6 } )
dxSetColorHSV( 180.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 4, 0, 3, 4, 3, 7 } )
dxSetColorHSV( 240.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 0, 4, 5, 0, 5, 1 } )
dxSetColorHSV( 300.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 2, 6, 7, 2, 7, 3 } )
dxPrint( -a-0.1, -a-0.1, -a-0.1, 1.0, 1.0, 1.0, "1" )
dxPrint( -a-0.1, -a-0.1, a+0.1, 1.0, 1.0, 1.0, "2" )
dxPrint( a+0.1, -a-0.1, a+0.1, 1.0, 1.0, 1.0, "3" )
dxPrint( a+0.1, -a-0.1, -a-0.1, 1.0, 1.0, 1.0, "4" )
dxPrint( -a-0.1, a+0.1, -a-0.1, 1.0, 1.0, 1.0, "5" )
dxPrint( -a-0.1, a+0.1, a+0.1, 1.0, 1.0, 1.0, "6" )
dxPrint( a+0.1, a+0.1, a+0.1, 1.0, 1.0, 1.0, "7" )
dxPrint( a+0.1, a+0.1, -a-0.1, 1.0, 1.0, 1.0, "8" )
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
Cube = Figure.new( function()
cube()
end )
E = Transformation.new( function()
end )
R4 = Transformation.new( function()
Rotate( 120.0, a, a, a )
end )
R5 = Transformation.new( function()
Rotate( 120.0, a,-a, a )
end )
R6 = Transformation.new( function()
Rotate( 120.0,-a,-a, a )
end )
R7 = Transformation.new( function()
Rotate( 120.0,-a, a, a )
end )
T1 = Transformation.new( function()
Translate( 2.0,-2.0, 0.0 )
end )
T2 = Transformation.new( function()
Translate(-2.0,-2.0, 0.0 )
end )
draw = E * Cube
draw = ( T1 * R4 ) * Cube
draw = ( T1^2 * R4^2 ) * Cube
draw = ( T1 * T2 * R5 ) * Cube
draw = ( T1^2 * T2 * R5^2 ) * Cube
draw = ( T1 * T2^2 * R6 ) * Cube
draw = ( T1^2 * T2^2 * R6^2 ) * Cube
draw = ( T1 * T2^3 * R7 ) * Cube
draw = ( T1^2 * T2^3 * R7^2 ) * Cube
tnNewObject()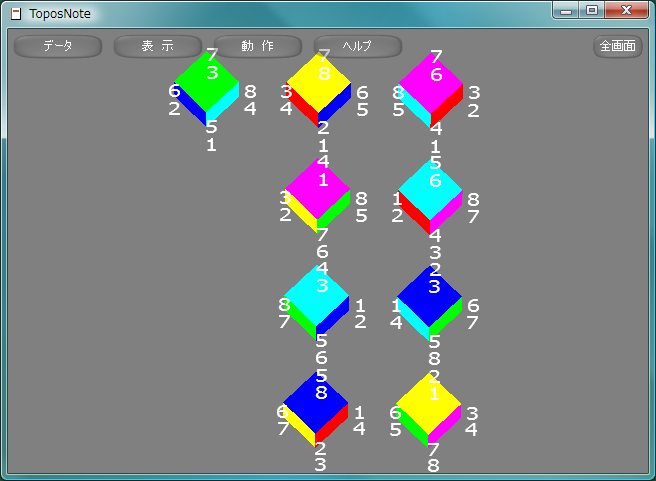
sample215c.lua
package.path = "std/?.lua"
require( "Geometry" )
a = math.sqrt( 3.0 ) / 3.0
vertices = {
-a, -a, -a, -a, -a, -a, 0.0, 0.0,
-a, -a, a, -a, -a, a, 0.0, 0.0,
a, -a, a, a, -a, a, 0.0, 0.0,
a, -a, -a, a, -a, -a, 0.0, 0.0,
-a, a, -a, -a, a, -a, 0.0, 0.0,
-a, a, a, -a, a, a, 0.0, 0.0,
a, a, a, a, a, a, 0.0, 0.0,
a, a, -a, a, a, -a, 0.0, 0.0
}
function cube()
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
dxSetColorHSV( 0.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 0, 1, 2, 0, 2, 3 } )
dxSetColorHSV( 60.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 1, 5, 6, 1, 6, 2 } )
dxSetColorHSV( 120.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 5, 4, 7, 5, 7, 6 } )
dxSetColorHSV( 180.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 4, 0, 3, 4, 3, 7 } )
dxSetColorHSV( 240.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 0, 4, 5, 0, 5, 1 } )
dxSetColorHSV( 300.0, 1.0, 1.0 )
dxTriangleMesh( 8, vertices, 2, { 2, 6, 7, 2, 7, 3 } )
dxPrint( -a-0.1, -a-0.1, -a-0.1, 1.0, 1.0, 1.0, "1" )
dxPrint( -a-0.1, -a-0.1, a+0.1, 1.0, 1.0, 1.0, "2" )
dxPrint( a+0.1, -a-0.1, a+0.1, 1.0, 1.0, 1.0, "3" )
dxPrint( a+0.1, -a-0.1, -a-0.1, 1.0, 1.0, 1.0, "4" )
dxPrint( -a-0.1, a+0.1, -a-0.1, 1.0, 1.0, 1.0, "5" )
dxPrint( -a-0.1, a+0.1, a+0.1, 1.0, 1.0, 1.0, "6" )
dxPrint( a+0.1, a+0.1, a+0.1, 1.0, 1.0, 1.0, "7" )
dxPrint( a+0.1, a+0.1, -a-0.1, 1.0, 1.0, 1.0, "8" )
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
Cube = Figure.new( function()
cube()
end )
E = Transformation.new( function()
end )
R8 = Transformation.new( function()
Rotate( 180.0, a, 0.0, a )
end )
R9 = Transformation.new( function()
Rotate( 180.0, 0.0, a, a )
end )
Ra = Transformation.new( function()
Rotate( 180.0,-a, 0.0, a )
end )
Rb = Transformation.new( function()
Rotate( 180.0, 0.0,-a, a )
end )
Rc = Transformation.new( function()
Rotate( 180.0, a, a, 0.0 )
end )
Rd = Transformation.new( function()
Rotate( 180.0,-a, a, 0.0 )
end )
T1 = Transformation.new( function()
Translate( 2.0,-2.0, 0.0 )
end )
T2 = Transformation.new( function()
Translate(-2.0,-2.0, 0.0 )
end )
draw = E * Cube
draw = ( T1 * R8 ) * Cube
draw = ( T1^2 * R9 ) * Cube
draw = ( T1^3 * Ra ) * Cube
draw = ( T1^4 * Rb ) * Cube
draw = ( T1 * T2 * Rc ) * Cube
draw = ( T1^2 * T2 * Rd ) * Cube
tnNewObject()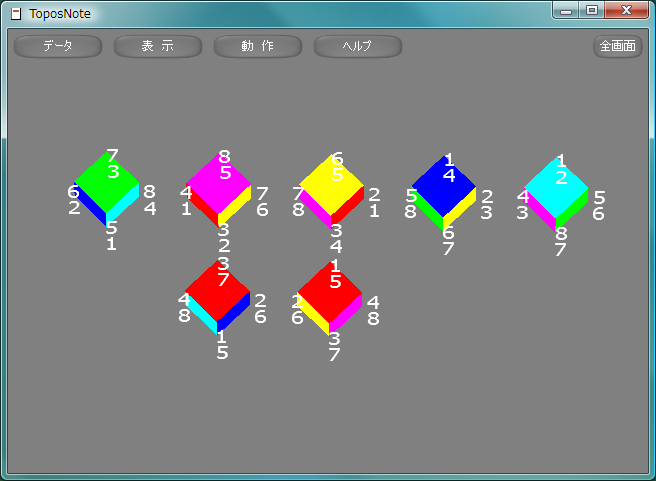
正八面体せいはちめんたい, regular octahedronを立方体に内接させると、正八面体の頂点と立方体の面、正八面体の面と立方体の頂点が1対1に対応する。この性質から、正八面体と立方体の対称変換群は同じものであることがわかる。
sample216.lua
package.path = "std/?.lua"
require( "Geometry" )
a = math.sqrt( 3.0 ) / 3.0
vertices = {
-a, -a, -a, -a, -a, -a, 0.0, 0.0,
-a, -a, a, -a, -a, a, 0.0, 0.0,
a, -a, a, a, -a, a, 0.0, 0.0,
a, -a, -a, a, -a, -a, 0.0, 0.0,
-a, a, -a, -a, a, -a, 0.0, 0.0,
-a, a, a, -a, a, a, 0.0, 0.0,
a, a, a, a, a, a, 0.0, 0.0,
a, a, -a, a, a, -a, 0.0, 0.0,
0.0, a, 0.0, 0.0, a, 0.0, 0.0, 0.0,
a, 0.0, 0.0, a, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, a, 0.0, 0.0, a, 0.0, 0.0,
-a, 0.0, 0.0, -a, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, -a, 0.0, 0.0, -a, 0.0, 0.0,
0.0, -a, 0.0, 0.0, -a, 0.0, 0.0, 0.0
}
function cube()
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
dxTriangleMesh( 14, vertices, 12, {
0, 1, 2, 0, 2, 3,
1, 5, 6, 1, 6, 2,
5, 4, 7, 5, 7, 6,
4, 0, 3, 4, 3, 7,
0, 4, 5, 0, 5, 1,
2, 6, 7, 2, 7, 3
} )
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
material_cube = {
0.4, 0.4, 0.4, 0.1,
1.0, 1.0, 1.0, 0.1,
0.0, 0.0, 0.0, 0.1,
0.001, 0.001, 0.001, 1.0,
16.0
}
function octahedron()
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
dxTriangleMesh( 14, vertices, 8, {
8, 9, 10,
8, 10, 11,
8, 11, 12,
8, 12, 9,
13, 9, 10,
13, 10, 11,
13, 11, 12,
13, 12, 9
} )
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
material_octahedron = {
0.0, 0.0, 0.0, 0.8,
1.0, 0.0, 0.0, 0.8,
0.0, 0.0, 0.0, 0.8,
0.001, 0.001, 0.001, 1.0,
16.0
}
dxSetRenderState( D3DRS_ALPHABLENDENABLE, 1 )
dxSetRenderState( D3DRS_SRCBLEND, D3DBLEND_SRCALPHA )
dxSetRenderState( D3DRS_DESTBLEND, D3DBLEND_INVSRCALPHA )
dxSetRenderState( D3DRS_FILLMODE, D3DFILL_SOLID )
SetMaterial( material_octahedron )
octahedron()
dxSetRenderState( D3DRS_FILLMODE, D3DFILL_WIREFRAME )
dxSetColor( 1.0, 0.0, 0.0 )
octahedron()
dxSetRenderState( D3DRS_FILLMODE, D3DFILL_SOLID )
SetMaterial( material_cube )
cube()
dxSetRenderState( D3DRS_FILLMODE, D3DFILL_WIREFRAME )
dxSetColor( 0.4, 0.4, 0.4 )
cube()
dxSetRenderState( D3DRS_FILLMODE, D3DFILL_SOLID )
dxSetRenderState( D3DRS_ALPHABLENDENABLE, 0 )
tnNewObject( "a001" )
Traj = {}
for i = 1, 72, 1 do
table.insert( Traj, 0.0 )
table.insert( Traj, 0.0 )
table.insert( Traj, 0.0 )
table.insert( Traj, -(i-1)*5.0 )
table.insert( Traj, 0.0 )
table.insert( Traj, 0.0 )
table.insert( Traj, (i-1)*100.0 )
end
tnSetTrajectory( "a001", 72, Traj ) 正十二面体せいじゅうにめんたい, regular dodecahedronは、正八面体と立方体の対応と同じように正二十面体せいにじゅうめんたい, regular icosahedronと対応する。
sample216.lua
package.path = "std/?.lua"
require("Geometry")
x = 0.525731112119133606
z = 0.850650808352039932
icosa = {
-x, z, 0.0,
x, z, 0.0,
-x, -z, 0.0,
x, -z, 0.0,
0.0, x, z,
0.0, -x, z,
0.0, x, -z,
0.0, -x, -z,
z, 0.0, x,
-z, 0.0, x,
z, 0.0, -x,
-z, 0.0, -x
}
v_icosa = {}
for i = 1, 36, 3 do
table.insert( v_icosa, icosa[i] )
table.insert( v_icosa, icosa[i+1] )
table.insert( v_icosa, icosa[i+2] )
table.insert( v_icosa, icosa[i] )
table.insert( v_icosa, icosa[i+1] )
table.insert( v_icosa, icosa[i+2] )
table.insert( v_icosa, 0.0 )
table.insert( v_icosa, 0.0 )
end
function icosahedron()
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
dxTriangleMesh( 12, v_icosa, 20, {
1, 4, 0,
4, 9, 0,
4, 5, 9,
8, 5, 4,
1, 8, 4,
1,10, 8,
10, 3, 8,
8, 3, 5,
3, 2, 5,
3, 7, 2,
3,10, 7,
10, 6, 7,
6,11, 7,
6, 0,11,
6, 1, 0,
10, 1, 6,
11, 0, 9,
2,11, 9,
5, 2, 9,
11, 2, 7
} )
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
material_icosa = {
0.4, 0.4, 0.4, 0.1,
1.0, 1.0, 1.0, 0.1,
0.0, 0.0, 0.0, 0.1,
0.001, 0.001, 0.001, 1.0,
16.0
}
dodeca = {}
function calc( i, a, b, c )
dodeca[3*i+1] = (icosa[3*a+1]+icosa[3*b+1]+icosa[3*c+1])/3.0
dodeca[3*i+2] = (icosa[3*a+2]+icosa[3*b+2]+icosa[3*c+2])/3.0
dodeca[3*i+3] = (icosa[3*a+3]+icosa[3*b+3]+icosa[3*c+3])/3.0
end
calc( 0, 1, 4, 0 )
calc( 1, 1, 8, 4 )
calc( 2, 8, 5, 4 )
calc( 3, 5, 9, 4 )
calc( 4, 4, 9, 0 )
calc( 5, 1, 10, 8 )
calc( 6, 10, 3, 8 )
calc( 7, 8, 3, 5 )
calc( 8, 3, 2, 5 )
calc( 9, 5, 2, 9 )
calc( 10, 10, 6, 7 )
calc( 11, 2, 11, 9 )
calc( 12, 11, 0, 9 )
calc( 13, 6, 0, 11 )
calc( 14, 6, 1, 0 )
calc( 15, 10, 1, 6 )
calc( 16, 3, 7, 2 )
calc( 17, 11, 2, 7 )
calc( 18, 3, 10, 7 )
calc( 19, 6, 11, 7 )
v_dodeca = {}
for i = 1, 60, 3 do
table.insert( v_dodeca, dodeca[i] )
table.insert( v_dodeca, dodeca[i+1] )
table.insert( v_dodeca, dodeca[i+2] )
table.insert( v_dodeca, dodeca[i] )
table.insert( v_dodeca, dodeca[i+1] )
table.insert( v_dodeca, dodeca[i+2] )
table.insert( v_dodeca, 0.0 )
table.insert( v_dodeca, 0.0 )
end
function dodecahedron()
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
dxTriangleMesh( 20, v_dodeca, 3, { 0, 1, 2, 0, 2, 3, 0, 3, 4 } )
dxTriangleMesh( 20, v_dodeca, 3, { 5, 6, 7, 5, 7, 2, 5, 2, 1 } )
dxTriangleMesh( 20, v_dodeca, 3, { 2, 7, 8, 2, 8, 9, 2, 9, 3 } )
dxTriangleMesh( 20, v_dodeca, 3, { 9, 8,16, 9,16,17, 9,17,11 } )
dxTriangleMesh( 20, v_dodeca, 3, { 4, 3, 9, 4, 9,11, 4,11,12 } )
dxTriangleMesh( 20, v_dodeca, 3, { 0, 4,12, 0,12,13, 0,13,14 } )
dxTriangleMesh( 20, v_dodeca, 3, {15, 5, 1,15, 1, 0,15, 0,14 } )
dxTriangleMesh( 20, v_dodeca, 3, {18,16, 8,18, 8, 7,18, 7, 6 } )
dxTriangleMesh( 20, v_dodeca, 3, {13,19,10,13,10,15,13,15,14 } )
dxTriangleMesh( 20, v_dodeca, 3, {19,17,16,19,16,18,19,18,10 } )
dxTriangleMesh( 20, v_dodeca, 3, {15,10,18,15,18, 6,15, 6, 5 } )
dxTriangleMesh( 20, v_dodeca, 3, {12,11,17,12,17,19,12,19,13 } )
dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
material_dodeca = {
0.0, 0.0, 0.0, 0.8,
1.0, 0.0, 0.0, 0.8,
0.0, 0.0, 0.0, 0.8,
0.001, 0.001, 0.001, 1.0,
16.0
}
dxSetRenderState( D3DRS_ALPHABLENDENABLE, 1 )
dxSetRenderState( D3DRS_SRCBLEND, D3DBLEND_SRCALPHA )
dxSetRenderState( D3DRS_DESTBLEND, D3DBLEND_INVSRCALPHA )
dxSetRenderState( D3DRS_FILLMODE, D3DFILL_SOLID )
SetMaterial( material_dodeca )
dodecahedron()
dxSetRenderState( D3DRS_FILLMODE, D3DFILL_WIREFRAME )
dxSetColor( 1.0, 0.0, 0.0, 0.8 )
dodecahedron()
dxSetRenderState( D3DRS_FILLMODE, D3DFILL_SOLID )
SetMaterial( material_icosa )
icosahedron()
dxSetRenderState( D3DRS_FILLMODE, D3DFILL_WIREFRAME )
dxSetColor( 0.4, 0.4, 0.4 )
icosahedron()
dxSetRenderState( D3DRS_FILLMODE, D3DFILL_SOLID )
dxSetRenderState( D3DRS_ALPHABLENDENABLE, 0 )
tnNewObject( "b001" )
Traj = {}
for i = 1, 72, 1 do
table.insert( Traj, 0.0 )
table.insert( Traj, 0.0 )
table.insert( Traj, 0.0 )
table.insert( Traj, -(i-1)*5.0 )
table.insert( Traj, 0.0 )
table.insert( Traj, 0.0 )
table.insert( Traj, (i-1)*100.0 )
end
tnSetTrajectory( "b001", 72, Traj )語 句
対称変換群 たいしょうへんかんぐん, symmetry transformation group対称群 たいしょうぐん, symmetric group
正四面体 せいしめんたい, regular tetrahedron
立方体 りっぽうたい, cube
正八面体 せいはちめんたい, regular octahedron
正十二面体 せいじゅうにめんたい, regular dodecahedron
正二十面体 せいにじゅうめんたい, regular icosahedron
Published by SANENSYA Co.,Ltd.