1.4 初等幾何作図法
著者:梅谷 武
語句:初等幾何の作図法について記す。
語句:初等幾何の作図法について記す。
弧, 円, 等辺, 直角, 等角, 有向線分
作成:2010-09-29
更新:2011-03-08
更新:2011-03-08
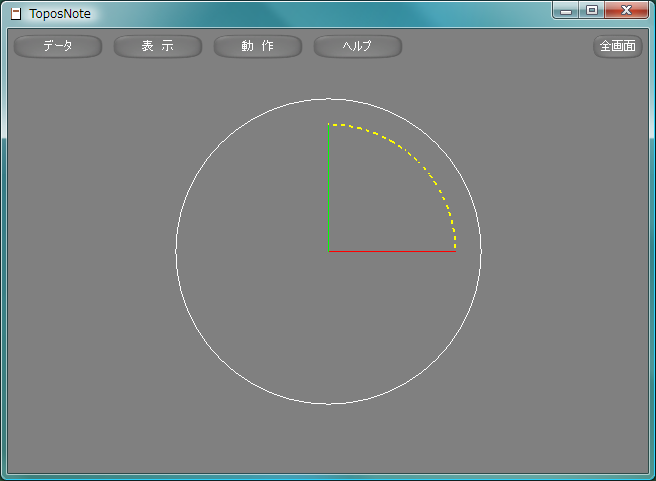
Arc関数は、ともに0でなく、方向が異なり、長さが等しい二つの位置ベクトルが与えられたときに、それらが定める平面上において、原点を中心とするそれらの終点どうしを結ぶ弧こ, arcを描く。弧は分割数の折れ線で近似される。この折れ線には直線と同じパラメータを設定することができる。
Arc
| 書式(1) | Arc( 始点, 終点, 分割数, 色 ) |
| 書式(2) | Arc( 始点, 終点, 分割数, 色, 太さ ) |
| 書式(3) | Arc( 始点, 終点, 分割数, 色, 太さ, 破線型H, 破線型L ) |
| 書式(4) | Arc( 始点, 終点, 分割数, 色, 太さ, 破線型H, 破線型L, 破線型係数 ) |
| 座標系 | 右手系 |
Circle関数はArc関数と同じ引数で円えん, circleを描く。
Circle
| 書式(1) | Circle( 始点, 終点, 分割数, 色 ) |
| 書式(2) | Circle( 始点, 終点, 分割数, 色, 太さ ) |
| 書式(3) | Circle( 始点, 終点, 分割数, 色, 太さ, 破線型H, 破線型L ) |
| 書式(4) | Circle( 始点, 終点, 分割数, 色, 太さ, 破線型H, 破線型L, 破線型係数 ) |
| 座標系 | 右手系 |
sample133.lua
package.path = "std/?.lua" require( "Geometry" ) white = Vector3.new( 1.0, 1.0, 1.0 ) yellow = Vector3.new( 1.0, 1.0, 0.0 ) AX = Vector3.new( 1.0, 0.0, 0.0 ) AY = Vector3.new( 0.0, 1.0, 0.0 ) Arc( AX, AY, 12, yellow, 2.0, 0xf0f0, 0xf0f0 ) Circle( 1.2*AX, 1.2*AY, 12, white, 1.0 ) tnNewObject()
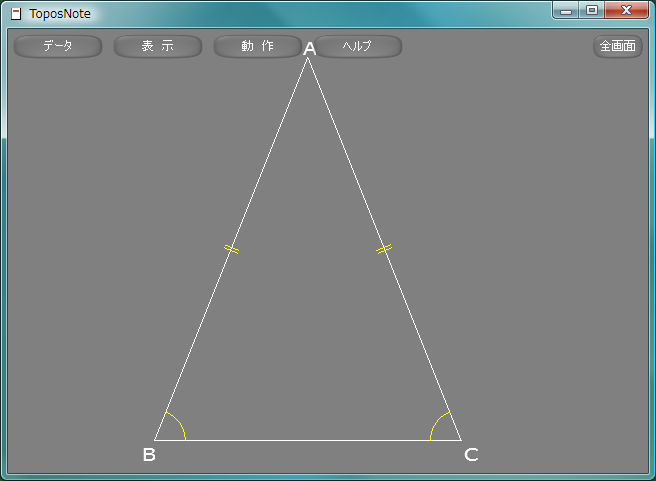
等辺とうへん, equilateralを表すために、LineCross関数が用意されている。角を表現するときはAngleArc関数を使う。
AngleArc
| 書式(1) | AngleArc( A, B, C, r, 分割数, 色 ) |
| 書式(2) | AngleArc( A, B, C, r, 分割数, 色, 太さ ) |
| 書式(3) | AngleArc( A, B, C, r, 分割数, 色, 太さ, 破線型H, 破線型L ) |
| 書式(4) | AngleArc( A, B, C, r, 分割数, 色, 太さ, 破線型H, 破線型L, 破線型係数 ) |
| 座標系 | 右手系 |
△ABCにおいて、∠ABCに対応するBを中心とする半径rの弧を描く。
LineCross
| 書式(1) | LineCross( A, B, C, l, n, 色 ) |
| 書式(2) | LineCross( A, B, C, l, n, 色, 太さ ) |
| 書式(3) | LineCross( A, B, C, l, n, 色, 太さ, 破線型H, 破線型L ) |
| 書式(4) | LineCross( A, B, C, l, n, 色, 太さ, 破線型H, 破線型L, 破線型係数 ) |
| 座標系 | 右手系 |
△ABCにおいて、辺ABの中央に直交する長さlの線をn(=1,2,3)本描く。
sample134.lua
package.path = "std/?.lua" require( "Geometry" ) white = Vector3.new( 1.0, 1.0, 1.0 ) yellow = Vector3.new( 1.0, 1.0, 0.0 ) A = Vector3.new( 2.0, 5.0, 0.0 ) B = Vector3.new( 0.0, 0.0, 0.0 ) C = Vector3.new( 4.0, 0.0, 0.0 ) dA = Vector3.new( -0.05, 0.25, 0.0 ) dB = Vector3.new( -0.15, -0.05, 0.0 ) dC = Vector3.new( 0.05, -0.05, 0.0 ) Line( A, B, white ) Line( B, C, white ) Line( C, A, white ) LineCross( A, B, C, 0.2, 2, yellow ) LineCross( C, A, B, 0.2, 2, yellow ) AngleArc( A, B, C, 0.4, 12, yellow ) AngleArc( A, C, B, 0.4, 12, yellow ) Print( A + dA, "A" ) Print( B + dB, "B" ) Print( C + dC, "C" ) tnNewObject()
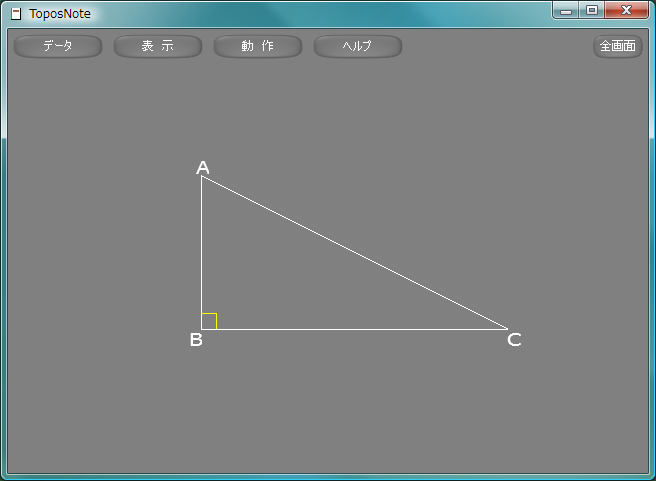
直角ちょっかく, right angleはRightAngle関数で表現する。
RightAngle
| 書式(1) | RightAngle( A, B, C, r, 色 ) |
| 書式(2) | RightAngle( A, B, C, r, 色, 太さ ) |
| 書式(3) | RightAngle( A, B, C, r, 色, 太さ, 破線型H, 破線型L ) |
| 書式(4) | RightAngle( A, B, C, r, 色, 太さ, 破線型H, 破線型L, 破線型係数 ) |
| 座標系 | 右手系 |
△ABCにおいて∠ABCが直角であるとき、辺長rの直角記号を描く。
sample135.lua
package.path = "std/?.lua" require( "Geometry" ) white = Vector3.new( 1.0, 1.0, 1.0 ) yellow = Vector3.new( 1.0, 1.0, 0.0 ) A = Vector3.new( 0.0, 2.0, 0.0 ) B = Vector3.new( 0.0, 0.0, 0.0 ) C = Vector3.new( 4.0, 0.0, 0.0 ) dA = Vector3.new( -0.05, 0.25, 0.0 ) dB = Vector3.new( -0.15, 0.0, 0.0 ) dC = Vector3.new( 0.00, 0.0, 0.0 ) Line( A, B, white ) Line( B, C, white ) Line( C, A, white ) RightAngle( A, B, C, 0.2, yellow ) Print( A + dA, "A" ) Print( B + dB, "B" ) Print( C + dC, "C" ) tnNewObject()
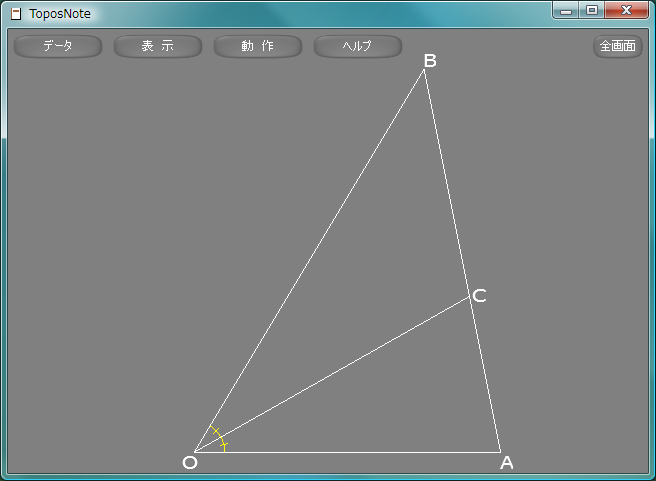
等角とうかく, equiangularを示すためにArcCross関数が用意されている。
ArcCross
| 書式(1) | ArcCross( A, B, C, r, l, n, 色 ) |
| 書式(2) | ArcCross( A, B, C, r, l, n, 色, 太さ ) |
| 書式(3) | ArcCross( A, B, C, r, l, n, 色, 太さ, 破線型H, 破線型L ) |
| 書式(4) | ArcCross( A, B, C, r, l, n, 色, 太さ, 破線型H, 破線型L, 破線型係数 ) |
| 座標系 | 右手系 |
△ABCにおいて、∠ABCに対応するBを中心とする半径rの弧を描き、その中央に直交する長さlの線をn(=1,2,3)本描く。
sample136.lua
package.path = "std/?.lua" require( "Geometry" ) white = Vector3.new( 1.0, 1.0, 1.0 ) yellow = Vector3.new( 1.0, 1.0, 0.0 ) A = Vector3.new( 4.0, 0.0, 0.0 ) B = Vector3.new( 3.0, 5.0, 0.0 ) O = Vector3.new( 0.0, 0.0, 0.0 ) C = ( T(B)*A + T(A)*B ) / ( T(A) + T(B) ) dA = Vector3.new( 0.00, 0.00, 0.0 ) dB = Vector3.new( 0.00, 0.25, 0.0 ) dC = Vector3.new( 0.05, 0.15, 0.0 ) dO = Vector3.new( -0.15, 0.00, 0.0 ) Line( O, A, white ) Line( O, B, white ) Line( O, C, white ) Line( A, B, white ) AngleArc( A, O, C, 0.4, 12, yellow ) AngleArc( B, O, C, 0.4, 12, yellow ) ArcCross( A, O, C, 0.4, 0.1, 1, yellow ) ArcCross( B, O, C, 0.4, 0.1, 1, yellow ) Print( A + dA, "A" ) Print( B + dB, "B" ) Print( C + dC, "C" ) Print( O + dO, "O" ) tnNewObject()
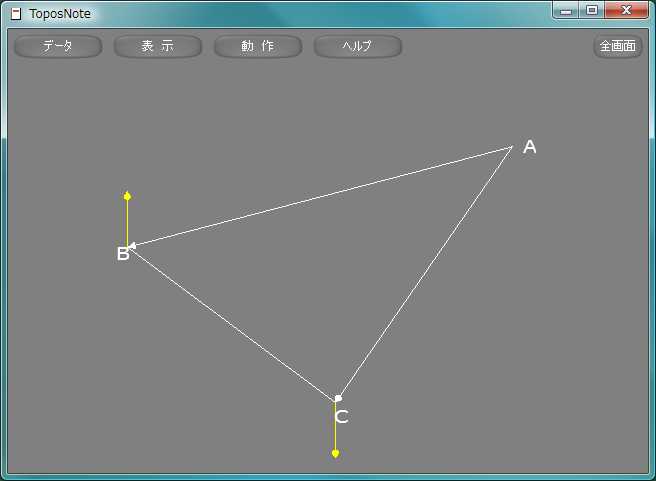
有向線分ゆうこうせんぶん, oriented segmentはArrow関数により描く。
Arrow
| 書式(1) | Arrow( 始点, 終点, 色 ) |
| 書式(2) | Arrow( 始点, 終点, 色, 太さ ) |
| 書式(3) | Arrow( 始点, 終点, 色, 太さ, 破線型H, 破線型L ) |
| 書式(4) | Arrow( 始点, 終点, 色, 太さ, 破線型H, 破線型L, 破線型係数 ) |
| 座標系 | 右手系 |
sample137.lua
package.path = "std/?.lua" require( "Geometry" ) white = Vector3.new( 1.0, 1.0, 1.0 ) yellow = Vector3.new( 1.0, 1.0, 0.0 ) A = Vector3.new( 2.0, 5.0, 0.0 ) B = Vector3.new( 0.0, 0.0, 0.0 ) C = Vector3.new( 4.0, 0.0, 0.0 ) dA = Vector3.new( -0.05, 0.25, 0.0 ) dB = Vector3.new( -0.15, -0.05, 0.0 ) dC = Vector3.new( 0.05, -0.05, 0.0 ) Arrow( A, B, white ) Arrow( A, C, white ) Line( B, C, white ) Arrow( B, B + Axis((A-B)/(C-B)), yellow ) Arrow( C, C + Axis((A-C)/(B-C)), yellow ) Print( A + dA, "A" ) Print( B + dB, "B" ) Print( C + dC, "C" ) tnNewObject()
語 句
弧 こ, arc円 えん, circle
等辺 とうへん, equilateral
直角 ちょっかく, right angle
等角 とうかく, equiangular
有向線分 ゆうこうせんぶん, oriented segment
Published by SANENSYA Co.,Ltd.