1.3 図形の変換
著者:梅谷 武
語句:図形の変換の仕方について記す。
語句:図形の変換の仕方について記す。
モデリング変換, 行列スタック, 並進, 回転, オイラー角, 四元数, 拡大縮小
作成:2010-09-28
更新:2011-03-08
更新:2011-03-08
図形を定義するときには、その図形そのものあるいはその部品をそれらが定義しやすい座標系で定義し、最終的に世界座標系にモデリング変換もでりんぐへんかん, modeling transformationする手法を使うのが一般的である。この場合、図形が階層構造をもつときに、上位のモデリング変換行列を一時的に行列スタックぎょうれつすたっく, matrix stackに退避し、下位のモデリング変換行列を適用後、退避していた行列を復帰して処理を進める。現在設定されているモデリング変換行列を、行列スタックに退避するのがPushMatrix関数、復帰するのがPopMatrix関数である。
このようなやり方で図形を定義する場合、行列スタックや変換行列の整合性は利用者に委ねられるため注意が必要である。
PushMatrix
| 書式 | PushMatrix() |
PopMatrix
| 書式 | PopMatrix() |
並進へいしん, translationはTranslate関数による。
Translate
| 書式 | Translate( x, y, z ) |
| 座標系 | 右手系 |
与えられた移動ベクトルに対応する並進行列を図形に作用させる。
sample128.lua
package.path = "std/?.lua" require( "Geometry" ) function Rect() SetMaterial( gold ) dxBox( 0.3, 0.2, 0.8 ) end Rect() PushMatrix() Translate( 2.0, 0.0, 0.0 ) Rect() PopMatrix() PushMatrix() Translate( 0.0, 2.0, 0.0 ) Rect() PopMatrix() PushMatrix() Translate( 0.0, 0.0, 2.0 ) Rect() PopMatrix() tnNewObject()
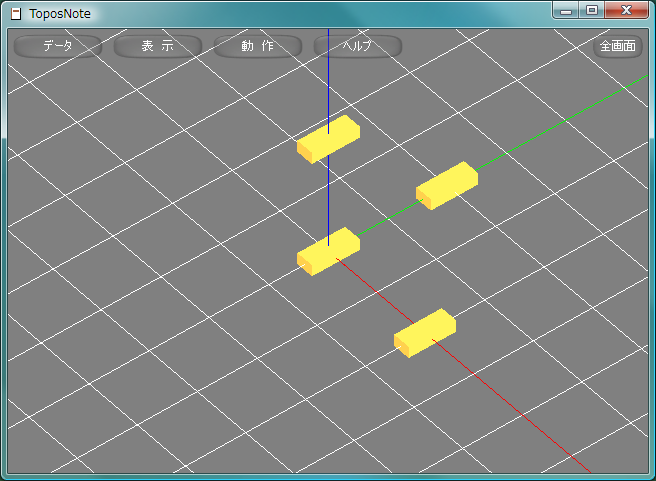
任意軸に関する回転かいてん, rotationはRotate関数、座標軸に関する回転はRotateX, RotateY, RotateZ関数による。
Rotate
| 書式 | Rotate( angle, x, y, z ) |
| 座標系 | 右手系 |
RotateX
| 書式 | RotateX( angle ) |
| 座標系 | 右手系 |
RotateY
| 書式 | RotateY( angle ) |
| 座標系 | 右手系 |
RotateZ
| 書式 | RotateZ( angle ) |
| 座標系 | 右手系 |
与えられた角度[度]と回転軸に対応する回転行列を図形に作用させる。
sample129.lua
package.path = "std/?.lua" require( "Geometry" ) function Rect() SetMaterial( gold ) dxBox( 0.3, 0.2, 0.8 ) end Rect() PushMatrix() Translate( 2.0, 0.0, 0.0 ) RotateX( 60.0 ) Rect() PopMatrix() PushMatrix() Translate( 0.0, 2.0, 0.0 ) RotateY( 60.0 ) Rect() PopMatrix() PushMatrix() Translate( 0.0, 0.0, 2.0 ) RotateZ( 60.0 ) Rect() PopMatrix() tnNewObject()
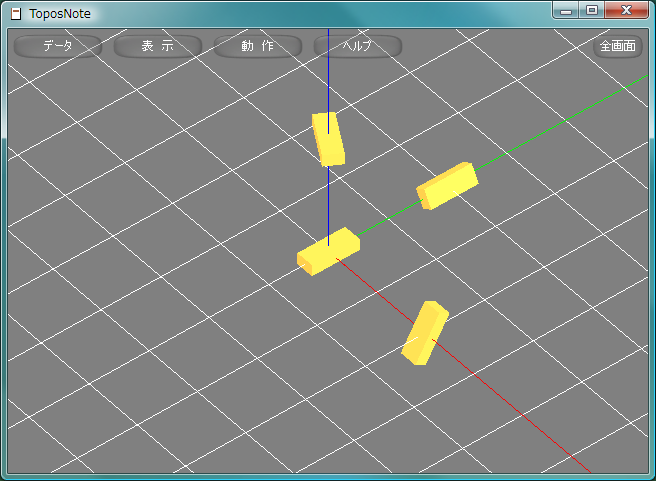
オイラー角おいらーかく, Euler angleによる変換は幾何ライブラリにより変換行列を計算し、MultMatrix関数あるいはdxMultMatrix関数により図形に作用させる。幾何ライブラリは右手系で計算し、MultMatrix関数は右手系の3×3変換行列を必要に応じて座標変換を施し、4×4変換行列としてプラットフォームに設定する。
dxMultMatrix関数はDirectXに直接、変換行列を設定するが、DirectXは左手系であることに注意しなければならない。
MultMatrix
| 書式 | MultMatrix( 3×3変換行列 ) |
| 座標系 | 右手系 |
dxMultMatrix
| 書式 | dxMultMatrix(m11,m12,m13,m14,...,m41,m42,m43,m44) |
| 座標系 | 左手系 |
sample130.lua
package.path = "std/?.lua" require( "Geometry" ) PI_180 = 3.14159265358979 / 180.0 function Rect() SetMaterial( gold ) dxBox( 0.3, 0.2, 0.8 ) end Rect() x = Matrix3x3.new( EulerAngles.new( 0.0, 60.0*PI_180, 0.0 ) ) PushMatrix() Translate( 2.0, 0.0, 0.0 ) MultMatrix( x ) Rect() PopMatrix() y = Matrix3x3.new( EulerAngles.new( 0.0, 0.0, 60.0*PI_180 ) ) PushMatrix() Translate( 0.0, 2.0, 0.0 ) MultMatrix( y ) Rect() PopMatrix() z = Matrix3x3.new( EulerAngles.new( 60.0*PI_180, 0.0, 0.0 ) ) PushMatrix() Translate( 0.0, 0.0, 2.0 ) MultMatrix( z ) Rect() PopMatrix() tnNewObject()
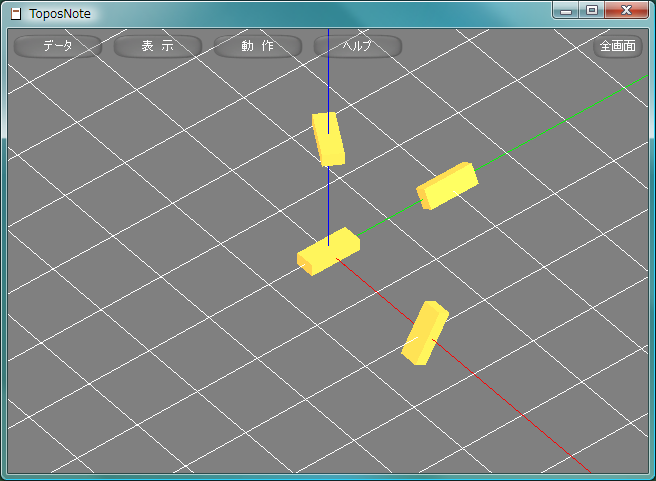
四元数しげんすう, quaternionによる変換も幾何ライブラリにより変換行列を計算し、MultMatrix関数により図形に作用させる。四元数による空間の回転を行なう場合、回転角は四元数の角の2倍になることに注意する。
sample131.lua
package.path = "std/?.lua" require( "Geometry" ) PI_180 = 3.14159265358979 / 180.0 function Rect() SetMaterial( gold ) dxBox( 0.3, 0.2, 0.8 ) end Rect() AX = Vector3.new( 1.0, 0.0, 0.0 ) AY = Vector3.new( 0.0, 1.0, 0.0 ) AZ = Vector3.new( 0.0, 0.0, 1.0 ) x = Matrix3x3.new( Quaternion.new( 30.0*PI_180, Axis(AZ/AY) ) ) PushMatrix() Translate( 2.0, 0.0, 0.0 ) MultMatrix( x ) Rect() PopMatrix() y = Matrix3x3.new( Quaternion.new( 30.0*PI_180, Axis(AX/AZ) ) ) PushMatrix() Translate( 0.0, 2.0, 0.0 ) MultMatrix( y ) Rect() PopMatrix() z = Matrix3x3.new( Quaternion.new( 30.0*PI_180, Axis(AY/AX) ) ) PushMatrix() Translate( 0.0, 0.0, 2.0 ) MultMatrix( z ) Rect() PopMatrix() tnNewObject()
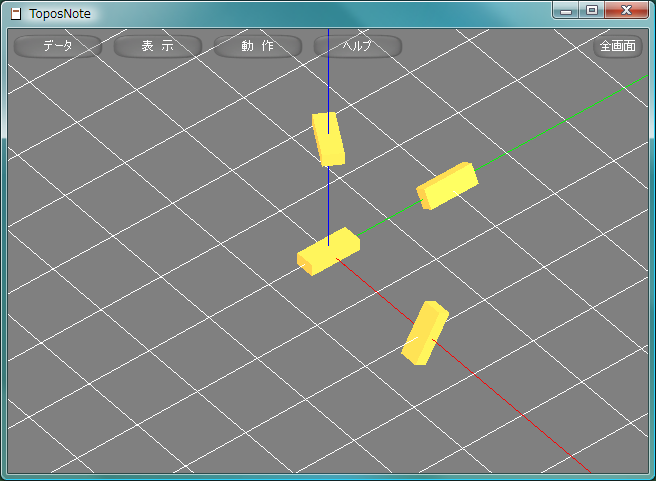
図形の座標軸方向の拡大縮小かくだいしゅくしょう, scalingはScale関数によって行なう。任意のアフィン変換は行列表現し、MultMatrix関数を使って行なう。
Scale
| 書式 | Scale( x, y, z ) |
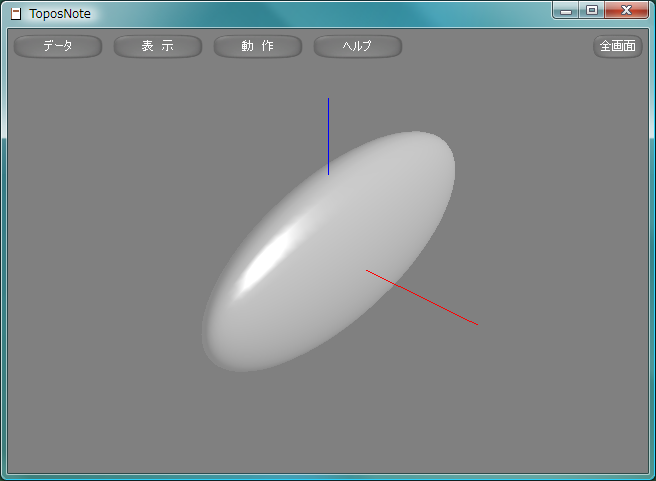
sample132.lua
package.path = "std/?.lua" require( "Geometry" ) PushMatrix() SetMaterial( chrome ) Scale( 0.5, 2.0, 1.0 ) dxSphere( 0.5, 36, 36 ) PopMatrix() tnNewObject()
語 句
モデリング変換 もでりんぐへんかん, modeling transformation行列スタック ぎょうれつすたっく, matrix stack
並進 へいしん, translation
回転 かいてん, rotation
オイラー角 おいらーかく, Euler angle
四元数 しげんすう, quaternion
拡大縮小 かくだいしゅくしょう, scaling
Published by SANENSYA Co.,Ltd.