5.1 図形の変換
著者:梅谷 武
語句:行列, オイラー角, 四元数
行列, オイラー角, 四元数を使って図形を変換する例を示す。
作成:2010-07-26
更新:2011-03-08
5.1 図形の変換
5.1.1 行列による変換
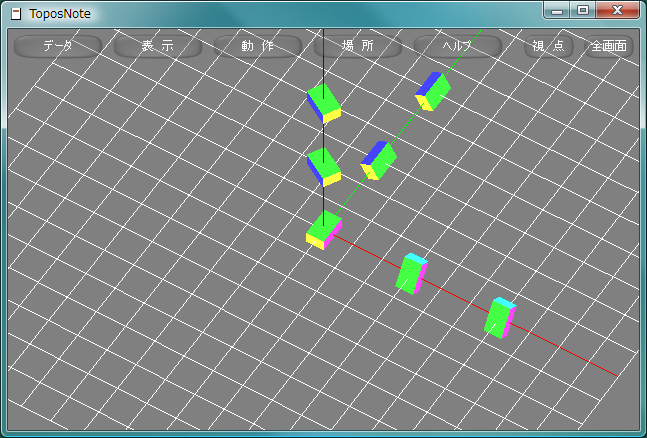
 MultMatrix命令により行列で回転を記述する方法と同等なRotate命令を示す。

sample501.lua

package.path = "std/?.lua"
require( "Geometry" )
PI_180 = 3.14159265358979 / 180.0
 
function cube()
  PushMatrix()
    Translate( 0.0, 0.0,-0.5 ); RotateX( -90.0 ); RotateY(  45.0 )
    dxSetColorHSV(   0.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.0,-0.5, 0.0 ); RotateX( 180.0 ); RotateY(  45.0 )
    dxSetColorHSV(  60.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.0, 0.0, 0.5 ); RotateX(  90.0 ); RotateY(  45.0 )
    dxSetColorHSV( 120.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.0, 0.5, 0.0 ); RotateY(  45.0 )
    dxSetColorHSV( 180.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate(-0.5, 0.0, 0.0 ); RotateZ(  90.0 ); RotateY(  45.0 )
    dxSetColorHSV( 240.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.5, 0.0, 0.0 ); RotateZ( -90.0 ); RotateY(  45.0 )
    dxSetColorHSV( 300.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
end
Rect = Figure.new( function()
  PushMatrix()
    Scale( 0.6, 1.0, 0.4 )
    cube()
  PopMatrix()
end )
E = Transformation.new( function()
  MultMatrix( Matrix3x3.new(
    1.0, 0.0, 0.0,
    0.0, 1.0, 0.0,
    0.0, 0.0, 1.0
  ) )
end )
sn = math.sin( 60.0 * PI_180 )
cn = math.cos( 60.0 * PI_180 )
RX = Transformation.new( function()
  MultMatrix( Matrix3x3.new(
    1.0, 0.0, 0.0,
    0.0,  cn, -sn,
    0.0,  sn,  cn
  ) )
end )
RX1 = Transformation.new( function()
  Rotate( 60.0, 1.0, 0.0, 0.0 )
end )
RY = Transformation.new( function()
  MultMatrix( Matrix3x3.new(
     cn, 0.0,  sn,
    0.0, 1.0, 0.0,
    -sn, 0.0,  cn
  ) )
end )
RY1 = Transformation.new( function()
  Rotate( 60.0, 0.0, 1.0, 0.0 )
end )
RZ = Transformation.new( function()
  MultMatrix( Matrix3x3.new(
     cn, -sn, 0.0,
     sn,  cn, 0.0,
    0.0, 0.0, 1.0
  ) )
end )
RZ1 = Transformation.new( function()
  Rotate( 60.0, 0.0, 0.0, 1.0 )
end )
TX = Transformation.new( function()
  Translate( 3.0, 0.0, 0.0 )
end )
TY = Transformation.new( function()
  Translate( 0.0, 3.0, 0.0 )
end )
TZ = Transformation.new( function()
  Translate( 0.0, 0.0, 3.0 )
end )
 
-- Drawing
draw =               E * Rect
draw =     ( TX * RX ) * Rect
draw =     ( TY * RY ) * Rect
draw =     ( TZ * RZ ) * Rect
draw =  ( TX^2 * RX1 ) * Rect
draw =  ( TY^2 * RY1 ) * Rect
draw =  ( TZ^2 * RZ1 ) * Rect
 
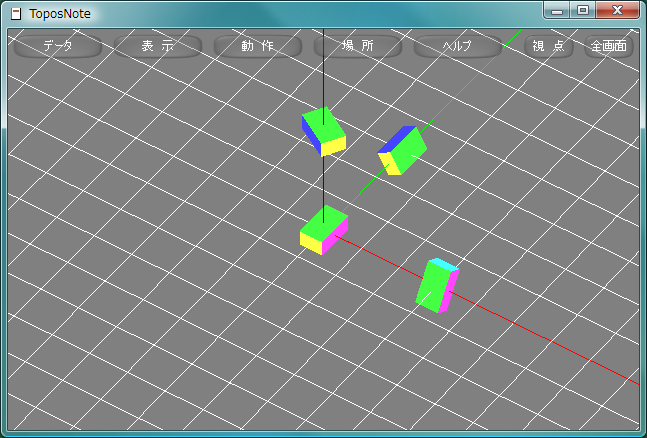
tnNewObject()
図5.1.1.4 sample501.lua
sample501.lua
5.1.2 オイラー角による変換
 オイラー角表現におけるX, Y, Z軸の組み合わせにはさまざまな種類がある。Lua拡張命令ではヨー・ピッチ・ロールと呼ばれる特に宇宙航空分野でよく使われる表現法のクラスが用意されている。

sample502.lua

package.path = "std/?.lua"
require( "Geometry" )
PI_180 = 3.14159265358979 / 180.0
 
function cube()
  PushMatrix()
    Translate( 0.0, 0.0,-0.5 ); RotateX( -90.0 ); RotateY(  45.0 )
    dxSetColorHSV(   0.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.0,-0.5, 0.0 ); RotateX( 180.0 ); RotateY(  45.0 )
    dxSetColorHSV(  60.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.0, 0.0, 0.5 ); RotateX(  90.0 ); RotateY(  45.0 )
    dxSetColorHSV( 120.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.0, 0.5, 0.0 ); RotateY(  45.0 )
    dxSetColorHSV( 180.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate(-0.5, 0.0, 0.0 ); RotateZ(  90.0 ); RotateY(  45.0 )
    dxSetColorHSV( 240.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.5, 0.0, 0.0 ); RotateZ( -90.0 ); RotateY(  45.0 )
    dxSetColorHSV( 300.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
end
Rect = Figure.new( function()
  PushMatrix()
    Scale( 0.6, 1.0, 0.4 )
    cube()
  PopMatrix()
end )
E = Transformation.new( function()
  MultMatrix( Matrix3x3.new(
    1.0, 0.0, 0.0,
    0.0, 1.0, 0.0,
    0.0, 0.0, 1.0
  ) )
end )
m = Matrix3x3.new( EulerAngles.new( 60.0*PI_180, 0.0, 0.0 ) )
RM = Transformation.new( function()
  MultMatrix( Matrix3x3.new(
    m.m11,m.m12,m.m13,
    m.m21,m.m22,m.m23,
    m.m31,m.m32,m.m33
  ) )
end )
TX = Transformation.new( function()
  Translate( 3.0, 0.0, 0.0 )
end )
TY = Transformation.new( function()
  Translate( 0.0, 3.0, 0.0 )
end )
TZ = Transformation.new( function()
  Translate( 0.0, 0.0, 3.0 )
end )
 
-- Drawing
draw =            E * Rect
draw =  ( TZ * RM ) * Rect
m = Matrix3x3.new( EulerAngles.new( 0.0, 60.0*PI_180, 0.0 ) )
draw =  ( TX * RM ) * Rect
m = Matrix3x3.new( EulerAngles.new( 0.0, 0.0, 60.0*PI_180 ) )
draw =  ( TY * RM ) * Rect
 
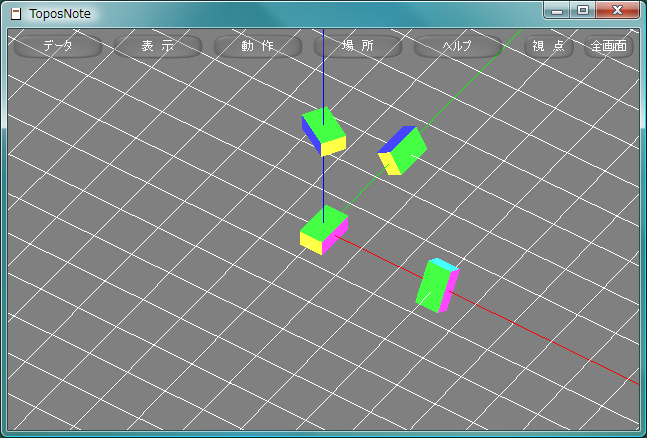
tnNewObject()
図5.1.2.4 sample502.lua
sample502.lua
5.1.3 四元数による変換
 四元数による空間の回転を行なう場合、回転角は四元数の角の2倍になることに注意する。

sample503.lua

package.path = "std/?.lua"
require( "Geometry" )
PI_180 = 3.14159265358979 / 180.0
 
function cube()
  PushMatrix()
    Translate( 0.0, 0.0,-0.5 ); RotateX( -90.0 ); RotateY(  45.0 )
    dxSetColorHSV(   0.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.0,-0.5, 0.0 ); RotateX( 180.0 ); RotateY(  45.0 )
    dxSetColorHSV(  60.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.0, 0.0, 0.5 ); RotateX(  90.0 ); RotateY(  45.0 )
    dxSetColorHSV( 120.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.0, 0.5, 0.0 ); RotateY(  45.0 )
    dxSetColorHSV( 180.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate(-0.5, 0.0, 0.0 ); RotateZ(  90.0 ); RotateY(  45.0 )
    dxSetColorHSV( 240.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
  PushMatrix()
    Translate( 0.5, 0.0, 0.0 ); RotateZ( -90.0 ); RotateY(  45.0 )
    dxSetColorHSV( 300.0, 0.8, 1.0 ); dxPolygon( 1.0, 4 )
  PopMatrix()
end
Rect = Figure.new( function()
  PushMatrix()
    Scale( 0.6, 1.0, 0.4 )
    cube()
  PopMatrix()
end )
E = Transformation.new( function()
  MultMatrix( Matrix3x3.new(
    1.0, 0.0, 0.0,
    0.0, 1.0, 0.0,
    0.0, 0.0, 1.0
  ) )
end )
AX = Vector3.new( 1.0, 0.0, 0.0 )
AY = Vector3.new( 0.0, 1.0, 0.0 )
AZ = Vector3.new( 0.0, 0.0, 1.0 )
m = Matrix3x3.new( Quaternion.new( 30.0*PI_180, Axis(AY/AX) ) )
RM = Transformation.new( function()
  MultMatrix( Matrix3x3.new(
    m.m11,m.m12,m.m13,
    m.m21,m.m22,m.m23,
    m.m31,m.m32,m.m33
  ) )
end )
TX = Transformation.new( function()
  Translate( 3.0, 0.0, 0.0 )
end )
TY = Transformation.new( function()
  Translate( 0.0, 3.0, 0.0 )
end )
TZ = Transformation.new( function()
  Translate( 0.0, 0.0, 3.0 )
end )
 
-- Drawing
draw =            E * Rect
draw =  ( TZ * RM ) * Rect
m = Matrix3x3.new( Quaternion.new( 30.0*PI_180, Axis(AX/AZ) ) )
draw =  ( TY * RM ) * Rect
m = Matrix3x3.new( Quaternion.new( 30.0*PI_180, Axis(AZ/AY) ) )
draw =  ( TX * RM ) * Rect
 
tnNewObject()
図5.1.3.4 sample503.lua
sample503.lua
Published by SANENSYA Co.,Ltd.