4.3 応用問題

著者:梅谷武
語句:航海術, 方位, 距離

球面三角法を使って航海術の問題を解く。

作成:2010-07-22
更新:2011-03-08

4.3 応用問題

4.3.1 航海術

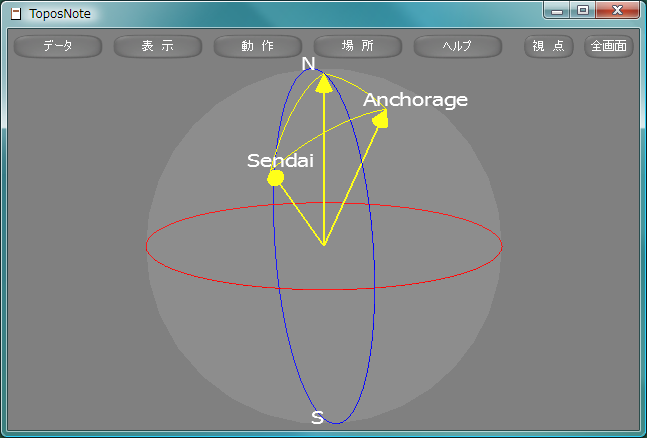
例題4.3.1.1 目的地への方位と距離

仙台(東経141°1'29",北緯38°16'12")からアンカレジ(西経149°54'6",北緯61°13'32")への方位と距離を求めよ。但し、地球は半径6378kmの球であるものとする。

sample403.lua

package.path = "std/?.lua"
require( "Geometry" )
 
PI_180 = 3.14159265358979 / 180.0
O  = Vector3.new( 0.0, 0.0, 0.0 )
N  = Vector3.new( 0.0, 0.0, 1.0 )
S  = Vector3.new( 0.0, 0.0,-1.0 )
R0 = Vector3.new( 0.0,-1.0, 0.0 )
R1 = Vector3.new( 1.0, 0.0, 0.0 )
R2 = Vector3.new( 0.0, 1.0, 0.0 )
R3 = Vector3.new(-1.0, 0.0, 0.0 )
function LatLng2Vec( lat, lng )
  if ( ( type( lat ) == "number" ) and ( type( lng ) == "number" ) ) then
    local i = lat * PI_180
    local k = lng * PI_180
    local q = Quaternion.new( k, N )
    if ( k < 0.0 ) then
      q = Quaternion.new( -k, S )
    end
    local s = V(q * R0)
    local r = Quaternion.new( i, Axis( N / s ) )
    return V( r * s )
  else
    return nil
  end
end
lat0 = Sex2Dec(  38, 16, 12 )
lng0 = Sex2Dec( 141,  1, 29 )
lat1 = Sex2Dec(  61, 13, 32 )
lng1 = Sex2Dec( 149, 54,  6 )
Sendai = LatLng2Vec( lat0, lng0 )
Anchor = LatLng2Vec( lat1, -lng1 )
red    = Vector3.new( 1.0, 0.0, 0.0 )
blue   = Vector3.new( 0.0, 0.0, 1.0 )
yellow = Vector3.new( 1.0, 1.0, 0.0 )
 
dxSetRenderState( D3DRS_ALPHABLENDENABLE, 1 )
dxSetRenderState( D3DRS_SRCBLEND, D3DBLEND_SRCALPHA )
dxSetRenderState( D3DRS_DESTBLEND, D3DBLEND_INVSRCALPHA )
Circle( R0, R1, 16, red )
Circle(  N, R0, 16, blue )
Arc( N, Sendai, 16, yellow )
Arc( N, Anchor, 16, yellow )
Arc( Sendai, Anchor, 16, yellow )
Arrow( O, N, yellow, 2.0 )
Arrow( O, Sendai, yellow, 2.0 )
Arrow( O, Anchor, yellow, 2.0 )
dxSetColor( 1.0, 1.0, 1.0, 0.1 )
dxSphere( 1.0, 32, 32 )
dxSetRenderState( D3DRS_ALPHABLENDENABLE, 0 )
 
dN = Vector3.new( 0.1,-0.1, 0.1 )
dS = Vector3.new( 0.1, 0.1, 0.1 )
dSen = Vector3.new( 0.1,-0.1, 0.1 )
dAnc = Vector3.new( 0.1,-0.1, 0.1 )
Print( N + dN, "N" )
Print( S + dS, "S" )
Print( Sendai + dSen, "Sendai" )
Print( Anchor + dAnc, "Anchorage" )
 
tnNewObject()

図4.3.1.4 sample403.lua

北極点をA、仙台をB、アンカレジをCとする球面三角形を描くと、A,b,cからB,aを求めることになる。これには余弦定理と正弦定理

cos a = cos b cos c + sin b sin c cos A

sin a

sin A

sin b

sin B

を使えばよい。

sample313.lua

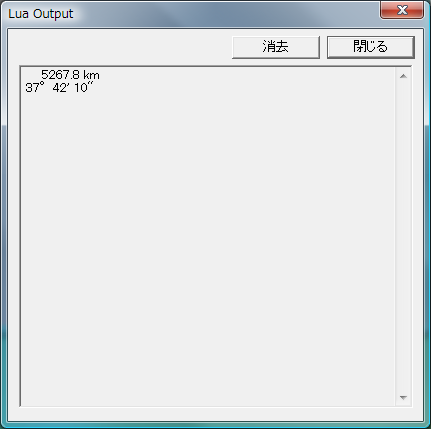
package.path = "std/?.lua"
require( "Geometry" )
 
PI = 3.14159265358979
PI_180 = 3.14159265358979 / 180.0
lat0 = Sex2Dec(  38, 16, 12 ) * PI_180
lng0 = Sex2Dec( 141,  1, 29 ) * PI_180
lat1 = Sex2Dec(  61, 13, 32 ) * PI_180
lng1 = Sex2Dec( 149, 54,  6 ) * PI_180
A = ( PI - lng0 ) + ( PI - lng1 )
b = PI / 2.0 - lat1
c = PI / 2.0 - lat0
 
cos_a = math.cos(b)*math.cos(c) + math.sin(b)*math.sin(c)*math.cos(A)
a = math.acos( cos_a )
printf( " %10.1f km\r\n", a*6378 )
sin_B = math.sin(b) * math.sin(A) / math.sin(a)
B = math.asin( sin_B )
v = Dec2Sex( B/PI_180 )
printf( [[ %d°%d' %d"]], v.x, v.y, v.z )

図4.3.1.8 sample404.lua

Published by SANENSYA Co.,Ltd.