4.1 球面三角形

著者:梅谷武
語句:大円, 小円, 弧, 軸, 極, 球面三角形, 頂点, 辺, 角, 極三角形

球面三角法で使われる用語を定義し、作図法を例示する。

作成:2010-07-22
更新:2021-04-25

球面と平面の交線は円である。この交線は平面が球の中心を通るときに大円だいえん, great circle、中心を通らないときに小円しょうえん, small circleと呼ばれる。

球面上に二点が与えられたとき、球の中心とこの二点が定める平面と球面の交線は大円となる。この二点を結ぶ直線が球の直径を与えるとき以外は、二点を結ぶ大円は一意的に決定する。この大円は二点によって二つの弧に分割されるが、その短い方を二点を結ぶ弧こ, arcと呼ぶ。

弧の長さは球の中心と両端の二点を結ぶ直線の成す角として定義される。単位球面のとき、すなわち半径が1のとき、角度を弧度法で表すことにすれば、弧の長さは曲線としての長さに一致する。

球面上の円の軸じく, axisとは、その円の中心を垂直に通る球の直径のことをいい、その軸の端点を極きょく, poleという。

二つの弧が交わるとき、その弧を含む平面どうしの平面角をその角という。これは交点における各接線の成す角に等しい。

4.1.2 球面三角形

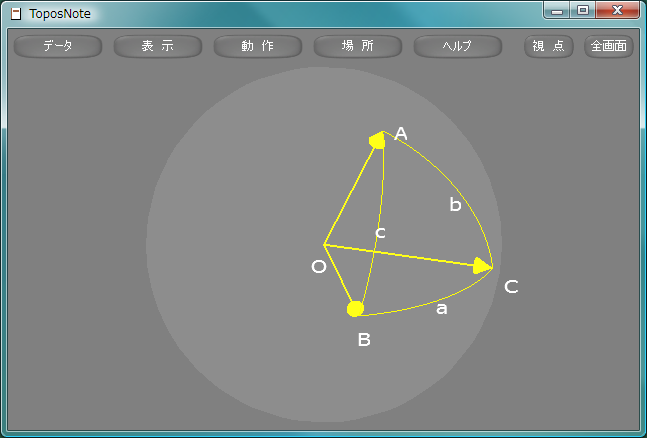
球面上の相異なる三点を結ぶ弧から成る図形を球面三角形きゅうめんさんかくけい, spherical triangleと呼ぶ。三点A, B, Cを頂点ちょうてん, vertex、三つの弧AB, BC, CAを辺へん, side、各頂点における二つの弧の成す角をその角かく, angleと呼ぶ。

sample401.lua

package.path = "std/?.lua"
require( "Geometry" )
 
PI = 3.14159265358979
s = math.sqrt( 3.0 ) / 2.0
A = Vector3.new( 0.5, 0.0,   s )
B = Vector3.new(   s,-0.5, 0.0 )
C = Vector3.new(   s, 0.5, 0.0 )
O = Vector3.new( 0.0, 0.0, 0.0 )
a = ( B + C ) / 1.8
b = ( C + A ) / 1.8
c = ( A + B ) / 1.8
yellow = Vector3.new( 1.0, 1.0, 0.0 )
 
dxSetRenderState( D3DRS_ALPHABLENDENABLE, 1 )
dxSetRenderState( D3DRS_SRCBLEND, D3DBLEND_SRCALPHA )
dxSetRenderState( D3DRS_DESTBLEND, D3DBLEND_INVSRCALPHA )
Arrow( O, A, yellow, 2.0 )
Arrow( O, B, yellow, 2.0 )
Arrow( O, C, yellow, 2.0 )
Arc( A, B, 32, yellow )
Arc( B, C, 32, yellow )
Arc( C, A, 32, yellow )
dxSetColor( 1.0, 1.0, 1.0, 0.1 )
dxSphere( 1.0, 32, 32 )
dxSetRenderState( D3DRS_ALPHABLENDENABLE, 0 )
 
dA = Vector3.new(  0.05,  0.05,  0.05 )
dB = Vector3.new(  0.05, -0.05, -0.05 )
dC = Vector3.new(  0.05,  0.05, -0.05 )
dO = Vector3.new( -0.1,  0.0,  -0.1 )
Print( A + dA, "A" )
Print( B + dB, "B" )
Print( C + dC, "C" )
Print( O + dO, "O" )
Print( a, "a" )
Print( b, "b" )
Print( c, "c" )
 
tnNewObject()

図4.1.2.4 sample401.lua

4.1.3 極三角形

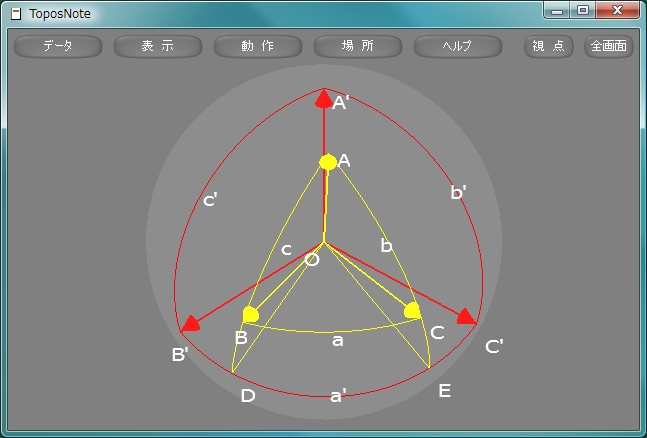
球面三角形ABCが与えられたとき、辺BC, CA, ABが定める大円の極でそれぞれA, B, Cと同じ側にあるものをA', B', C'とする。このとき球面三角形A'B'C'を球面三角形ABCの極三角形きょくさんかくけい, polar triangleという。

α = [OA], β = [OB], γ = [OC], α' = [OA'], β' = [OB'], γ' = [OC']とおくと、球面三角形A'B'C'が球面三角形ABCの極三角形であることを次のように表現できる。

α' ⊥ β, α' ⊥ γ

β' ⊥ γ, β' ⊥ α

γ' ⊥ α, γ' ⊥ β

これを並べ替えると

α ⊥ β', α ⊥ γ'

β ⊥ γ', β ⊥ α'

γ ⊥ α', γ ⊥ β'

となり、これは球面三角形ABCが球面三角形A'B'C'の極三角形であることを意味している。

命題4.1.3.3 極三角形の相反性

球面三角形A'B'C'が球面三角形ABCの極三角形であれば、球面三角形ABCは球面三角形A'B'C'の極三角形である

球面三角形A'B'C'が球面三角形ABCの極三角形であるとき、大円ABと大円B'C'の交点をD、大円ACと大円B'C'の交点をEとする。C'は大円ABの極であるから辺∠DOC' = π/2であり、B'は大円ACの極であるから辺∠EOB' = π/2である。したがって

∠DOC' + ∠EOB' = ∠B'OC' + ∠DOE = a' + A = π

が成り立つ。同様にして次の命題が成り立つことがわかる。

命題4.1.3.5 極三角形の辺と角の相補性

球面三角形A'B'C'が球面三角形ABCの極三角形であれば次が成り立つ。

(4.1)

a' + A = b' + B = c' + C = π

(4.2)

a + A' = b + B' = c + C' = π

sample402.lua

package.path = "std/?.lua"
require( "Geometry" )
 
PI = 3.14159265358979
s = math.sqrt( 3.0 ) / 2.0
A = Vector3.new( 0.5, 0.0,   s )
B = Vector3.new(   s,-0.5, 0.0 )
C = Vector3.new(   s, 0.5, 0.0 )
O = Vector3.new( 0.0, 0.0, 0.0 )
a = ( B + C ) / 1.8
b = ( C + A ) / 1.8
c = ( A + B ) / 1.8
A1 = Axis( C / B )
B1 = Axis( A / C )
C1 = Axis( B / A )
a1 = ( B1 + C1 ) / 1.2
b1 = ( C1 + A1 ) / 1.2
c1 = ( A1 + B1 ) / 1.2
red    = Vector3.new( 1.0, 0.0, 0.0 )
yellow = Vector3.new( 1.0, 1.0, 0.0 )
 
dxSetRenderState( D3DRS_ALPHABLENDENABLE, 1 )
dxSetRenderState( D3DRS_SRCBLEND, D3DBLEND_SRCALPHA )
dxSetRenderState( D3DRS_DESTBLEND, D3DBLEND_INVSRCALPHA )
Arrow( O, A, yellow, 2.0 )
Arrow( O, B, yellow, 2.0 )
Arrow( O, C, yellow, 2.0 )
Arc( A, B, 32, yellow )
Arc( B, C, 32, yellow )
Arc( C, A, 32, yellow )
q = Quaternion.new( PI / 2.0, Axis( B / A ) )
D = V( q * A )
r = Quaternion.new( PI / 2.0, Axis( C / A ) )
E = V( r * A )
Arc( B, D, 32, yellow )
Arc( C, E, 32, yellow )
Line( O, D, yellow )
Line( O, E, yellow )
Arrow( O, A1, red, 2.0 )
Arrow( O, B1, red, 2.0 )
Arrow( O, C1, red, 2.0 )
Arc( A1, B1, 32, red )
Arc( B1, C1, 32, red )
Arc( C1, A1, 32, red )
dxSetColor( 1.0, 1.0, 1.0, 0.1 )
dxSphere( 1.0, 32, 32 )
dxSetRenderState( D3DRS_ALPHABLENDENABLE, 0 )
 
dA = Vector3.new(  0.05,  0.05,  0.05 )
dB = Vector3.new(  0.05, -0.05,  0.0  )
dC = Vector3.new(  0.05,  0.05,  0.0  )
dD = Vector3.new(  0.05,  0.05, -0.05 )
dE = Vector3.new(  0.05,  0.05, -0.05 )
dO = Vector3.new( -0.1, -0.1,  -0.1 )
dA1 = Vector3.new(  0.05,  0.05,  0.0  )
dB1 = Vector3.new(  0.05, -0.05, -0.05 )
dC1 = Vector3.new(  0.05,  0.05, -0.05 )
Print( A + dA, "A" )
Print( B + dB, "B" )
Print( C + dC, "C" )
Print( D + dD, "D" )
Print( E + dE, "E" )
Print( O + dO, "O" )
Print( a, "a" )
Print( b, "b" )
Print( c, "c" )
Print( A1 + dA1, "A'" )
Print( B1 + dB1, "B'" )
Print( C1 + dC1, "C'" )
Print( a1, "a'" )
Print( b1, "b'" )
Print( c1, "c'" )
 
tnNewObject()

図4.1.3.8 sample402.lua

4.1.4 参考文献

[1] Isaac Todhunter, Spherical Trigonometry, MACMILLAN AND CO., 1863

[2] Charles Jasper Joly, A manual of quaternions, Franklin Classics, 1905(2018)

[3] 長谷川一郎, 天文計算入門―球面三角から軌道計算まで, 恒星社厚生閣, 1997

[4] 堀源一郎, ハミルトンと四元数―人・数の体系・応用, 海鳴社, 2007

数　　学

大円だいえん, great circle
小円しょうえん, small circle
弧こ, arc
軸じく, axis
極きょく, pole
球面三角形きゅうめんさんかくけい, spherical triangle
頂点ちょうてん, vertex
辺へん, side
角かく, angle
極三角形きょくさんかくけい, polar triangle

Published by SANENSYA Co.,Ltd.