3.3 正弦・余弦定理
著者:梅谷 武
語句:正弦定理, 第一余弦定理, 第二余弦定理
ベクトルの代数的性質を使って、正弦定理と余弦定理を証明する。
作成:2010-07-18
更新:2011-03-08
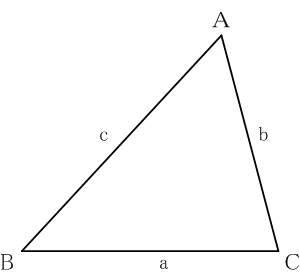
三角形の各頂角の正弦と対辺の比は一定である。すなわち、三角形
ABCにおいて
∠Aの対辺を
a、
∠Bの対辺を
b、
∠Cの対辺を
cとすると次が成り立つ。
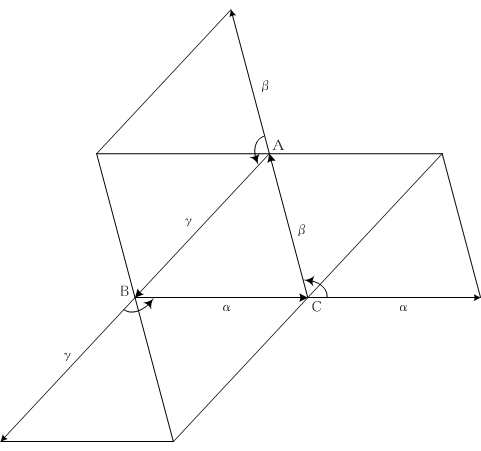
α := [BC], β := [CA],
γ := [AB]とおく。
上図より、
大きさを比べると
| TαTβ sin(π - C) =
TβTγ sin(π - A) =
TγTα sin(π - B)
|
これを書き直すと
| ab sinC = bc sinA = ca sinB
|
これを
abcで割ると
この逆比をとれば正弦定理が得られる。
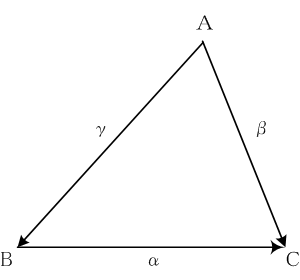
α := [BC], β := [AC],
γ := [AB]とおくと
α = β - γより、
| α ∙ α = (β - γ)(β - γ) =
β ∙ β - γ ∙ β - β ∙ γ + γ ∙ γ
|
内積とベクトル積で展開するとスカラー部だけが残り次のようになる。
| 〈 α, α 〉 =
〈 β, β 〉 + 〈 γ, γ 〉
- 2〈 β, γ 〉
|