3.2 三角形とベクトル比
著者:梅谷 武
語句:三角形, ベクトル比, 二等辺三角形, 底角, 内角, 二等分線
ベクトル比を使って三角形の問題を解く。
作成:2010-07-15
更新:2011-03-08
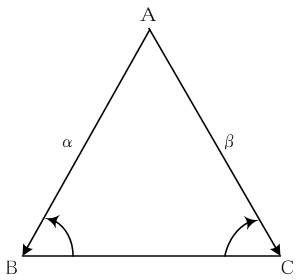
二等辺三角形の二つの底角は等しい。すなわち、三角形
ABCにおいて
AB = ACならば
∠B = ∠Cが成り立つ。
三角形は二辺とその挟む角により決定されるから、例えば
BC,
BAを与えることにより定まる。これは
BCとベクトル比
を与えることと同等である。
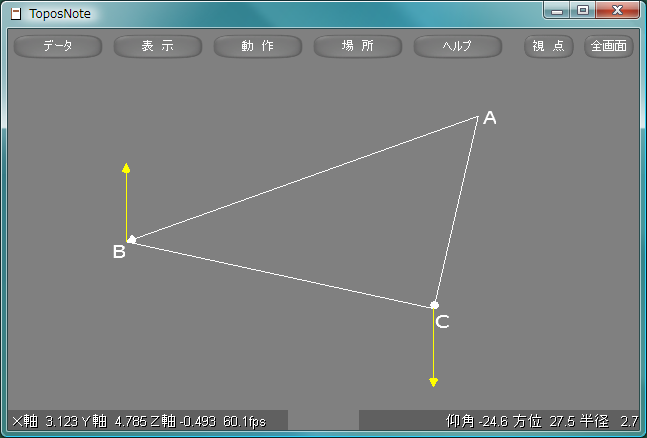
α := [AB], β := [AC]とおくと、次が成り立つ。
ここで、
Tα = Tβならば
〈α,α〉 = 〈β,β〉であるから、二つのベクトル比は互いに共役である。
これは角度が等しく、軸が反転していることを意味している。
package.path = "std/?.lua"
require( "Geometry" )
A = Vector3.new( 2.0, 5.0, 0.0 )
B = Vector3.new( 0.0, 0.0, 0.0 )
C = Vector3.new( 4.0, 0.0, 0.0 )
white = Vector3.new( 1.0, 1.0, 1.0 )
yellow = Vector3.new( 1.0, 1.0, 0.0 )
A = Vector3.new( 2.0, 5.0, 0.0 )
B = Vector3.new( 0.0, 0.0, 0.0 )
C = Vector3.new( 4.0, 0.0, 0.0 )
dA = Vector3.new( -0.05, 0.25, 0.0 )
dB = Vector3.new( -0.15, -0.05, 0.0 )
dC = Vector3.new( 0.05, -0.05, 0.0 )
Arrow( A, B, white )
Arrow( A, C, white )
Line( B, C, white )
Arrow( B, B + Axis((A-B)/(C-B)), yellow )
Arrow( C, C + Axis((A-C)/(B-C)), yellow )
Print( A + dA, "A" )
Print( B + dB, "B" )
Print( C + dC, "C" )
tnNewObject()
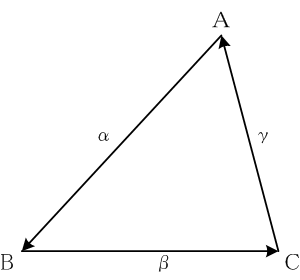
三角形の内角の和は
2∠Rに等しい。すなわち、三角形
ABCにおいて
∠A + ∠B + ∠C = 2∠Rが成り立つ。
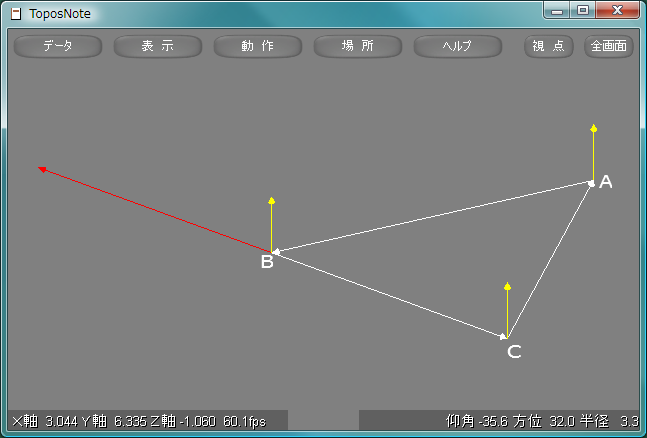
三角形の各頂点におけるベクトル比
を平面上のベクトル変換として合成すると
となり、これはベクトルの反転、すなわち180度の回転となっている。
package.path = "std/?.lua"
require( "Geometry" )
A = Vector3.new( 3.0, 4.0, 0.0 )
B = Vector3.new( 0.0, 0.0, 0.0 )
C = Vector3.new( 4.0, 0.0, 0.0 )
white = Vector3.new( 1.0, 1.0, 1.0 )
yellow = Vector3.new( 1.0, 1.0, 0.0 )
red = Vector3.new( 1.0, 0.0, 0.0 )
A = Vector3.new( 3.0, 4.0, 0.0 )
B = Vector3.new( 0.0, 0.0, 0.0 )
C = Vector3.new( 4.0, 0.0, 0.0 )
dA = Vector3.new( -0.05, 0.25, 0.0 )
dB = Vector3.new( -0.15, -0.05, 0.0 )
dC = Vector3.new( 0.05, -0.05, 0.0 )
Arrow( A, B, white )
Arrow( B, C, white )
Arrow( C, A, white )
Line( B, C, white )
Arrow( A, A + Axis((C-A)/(B-A)), yellow )
Arrow( B, B + Axis((A-B)/(C-B)), yellow )
Arrow( C, C + Axis((B-C)/(A-C)), yellow )
q = ((A-B)/(C-B))*((B-C)/(A-C))*((C-A)/(B-A))
Arrow( B, B + V(q*(C-B)), red )
Print( A + dA, "A" )
Print( B + dB, "B" )
Print( C + dC, "C" )
tnNewObject()
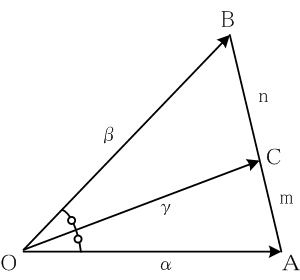
三角形の内角の二等分線は対辺をその角を挟む二辺と同じ比に内分する。すなわち、三角形
ABOにおいて、角
Oの二等分線と対辺の交点を
Cとすれば、
OA : OB = AC : CBが成り立つ。
AC:CBを実数比
m:nで表すと
ベクトル比
γ/αをベクトル
γに左から作用させると、
βと重なることから
これに上の式を代入し、整理すると
| n2 | | + m2 | | = s(m + n)2 -2mn
∈ ℝ
|
となり、左辺のベクトル部は
0であることから次が成り立つ。
package.path = "std/?.lua"
require( "Geometry" )
white = Vector3.new( 1.0, 1.0, 1.0 )
yellow = Vector3.new( 1.0, 1.0, 0.0 )
A = Vector3.new( 4.0, 0.0, 0.0 )
B = Vector3.new( 3.0, 5.0, 0.0 )
O = Vector3.new( 0.0, 0.0, 0.0 )
C = ( T(B)*A + T(A)*B ) / ( T(A) + T(B) )
dA = Vector3.new( 0.00, 0.00, 0.0 )
dB = Vector3.new( 0.00, 0.25, 0.0 )
dC = Vector3.new( 0.05, 0.15, 0.0 )
dO = Vector3.new( -0.15, 0.00, 0.0 )
Line( O, A, white )
Line( O, B, white )
Line( O, C, white )
Line( A, B, white )
AngleArc( A, O, C, 0.4, 12, yellow )
AngleArc( B, O, C, 0.4, 12, yellow )
ArcCross( A, O, C, 0.4, 0.1, 1, yellow )
ArcCross( B, O, C, 0.4, 0.1, 1, yellow )
Print( A + dA, "A" )
Print( B + dB, "B" )
Print( C + dC, "C" )
Print( O + dO, "O" )
tnNewObject()