2.3 補間法
著者:梅谷 武
語句:四元数,対数,指数,冪乗,球面線形補間,slerp
作成:2010-06-05
更新:2011-03-08
2.3 補間法
2.3.1 四元数の指数関数と対数関数
 四元数の対数たいすう, logarithm関数は次のように定義される。
log:S3-{±1} → V3×,  q = cos∠q + sin∠qUVq ↦ log q := ∠qUVq
 四元数の指数しすう, exponent関数は次のように定義される。
exp: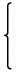V3 → S3,  α ↦ exp α
exp α := lc72
1,
α = 0
cosθ+sinθ∙ν,
α = (θ+2nπ)ν, θ∈(0,π), n∈ℤ, Tν=1
指数関数はα = 0において連続である。

命題2.3.1.3

exp(log q) = q,  q ∈ S3-{±1}
 四元数の冪乗べきじょう, powerを次のように定義する。
qt = exp(t log q),  t ∈ ℝ
2.3.2 球面線形補間
 球面線形補間きゅうめんせんけいほかん, spherical linear interpolationとは二つの姿勢を表わすベルソルを滑らかに補間する方法の一つである。英語表記を略してslerpspherical linear interpolationの略記と呼ばれる。[1]
 q0,q1∈S3, t∈[0,1]のとき、球面線形補間は次の関数により定義される。
slerp(q0, q1, t) := (q1q0-1)tq0
q1q0-1を極形式表現すると、
(q1q0-1)t
=
cos tθ + sin tθ ∙ ν
=
sin θ cos tθ - sin tθ cos θ + sin tθ cos θ
sin θ
 +
sin tθ sin θ
sin θ
ν
=
sin (1-t)θ
sin θ
 +
sin tθ
sin θ
(cos θ + sin θ ∙ ν)
=
sin (1-t)θ
sin θ
 +
sin tθ
sin θ
q1q0-1
右からq0をかけることにより、次の公式が得られる。

命題2.3.2.3 slerp公式

q0,q1∈S3, t∈[0,1]のとき、q1q0-1の角度をθ∈(0,π)とすると、
(2.1)
slerp(q0, q1, t) =
sin (1-t)θ
sin θ
q0 +
sin tθ
sin θ
q1
 slerp曲線は必ずしも最短にはならず、最短曲線を求めるには次の制約条件を課すことが必要である。

命題2.3.2.5 slerpの最短条件

q0,q1∈S3, t∈[0,1]のとき、Sq0q1が負でなければ、slerp(q0, q1, t)はq0とq1を結ぶ最短曲線となる。
2.3.3 参考文献
[1] Ken Shoemake, Animating rotation with quaternion curves, ACM SIGGRAPH Computer Graphics, vol.19, no.3, pp.245-254, 1985-07
数　　学
対数 たいすう, logarithm
指数 しすう, exponent
冪乗 べきじょう, power
球面線形補間 きゅうめんせんけいほかん, spherical linear interpolation
slerp spherical linear interpolationの略記
 
Published by SANENSYA Co.,Ltd.