2.2節 正多角形
著者:梅谷 武
語句:正多角形, 対称性, 対称変換群, 対称群, 交代群, 正二面体群
正多角形の対称変換群を決定し、正三角形・正方形・正五角形の対称変換群を群論的作図法で可視化する。
作成:2010-01-18
更新:2021-07-01
2.2 正多角形
2.2.1 平面図形の対称性
 我々がある平面図形が対称であるという場合、通常、その図形を平面内のある点を中心として回転させると元の図形に一致する点対称と、図形内を通るをある直線を軸として空間内を180度回転させると元の図形に一致する線対称の２種類を思い浮かべます。これはその図形が平面あるいは空間内の合同変換により不変であると言い換えることができます。群論の観点からは、図形の対称性は次のように定義されます。

定義2.2.1.2 図形の対称性

図形の対称性たいしょうせい, symmmetryは、その図形を不変にする平面あるいは空間内の合同変換の群れにより特徴付けられ、これらは平面(E,V2)の合同変換群Cong(E) ≅ Trans(E) ⋊ O(V2)あるいは空間(U,V3)の合同変換群Cong(U) ≅ Trans(U) ⋊ O(V3)の部分群を成し、これを対称変換群たいしょうへんかんぐん, symmetry transformation groupと呼ぶ。
 正多角形のような有界な図形の場合、対称変換は直交変換となりますが、結晶の対称性を考える場合は平行移動が対称変換になります。
2.2.2 対称群
 多角形の合同変換は、その頂点の置換を引き起こすことから、対称変換群は、紛らわしい用語ですが頂点集合の置換全体から成る対称群に埋め込むことができます。ここでは対称群について簡単に復習しておきます。
 n個の置換ちかん, permutationとは、n個の数{1,2,⋯,n}の並べ替え
σ = lb48
1
2
⋯
n
σ(1)
σ(2)
⋯
σ(n)
rb48
のことです。上段と下段は並べ替えの前と後に対応します。これは全単射
σ:{1,2,⋯,n} longrightarrow {1,2,⋯,n},  i longmapsto σ(i)
と同じもので、n個の置換全体の集合は写像の合成に関して群をなし、これを対称群たいしょうぐん, symmetric groupSnといいます。対称群Snは位数いすう, ordern!の有限群です。
 対称群Snにおいて互換ごかん, transpositionとは二つの数を入れ替える置換のことです。すべての置換は有限個の互換の積で表現することができます。この表現は一意ではありませんが、その表現を構成する互換の数が奇数か偶数かということは表現によらずに定まります。このとき、互換の数が偶数のものを偶置換ぐうちかん, even permutation、奇数のものを奇置換きちかん, odd permutationといいます。
 置換σに対して、その符号ふごう, signatureを
sgn(σ) := lc48
1
σが偶置換のとき
-1
σが奇置換のとき
と定めます。
sgn(σ1σ2) = sgn(σ1)sgn(σ2),  σ1, σ2 ∈ Sn
が成り立ちますから、sgn:Sn → {1, -1}は準同型であり、その核An := { σ ∈ Sn | sgn = 1 }はSnの正規部分群となります。偶置換の全体から成るこの群を交代群こうたいぐん, alternating groupといいます。交代群Anは位数n!/2です。
2.2.3 合同変換群の有限部分群
 平面あるいは空間上の合同変換群の有限部分群をGとしましょう。平面あるいは空間上に原点Oと原点と異なる任意の点Pを定めます。軌道
GP := { gP | g ∈ G } = { P1 :=P, P2, ⋯, Pn }
は有限個の点です。この重心をCとします。
OC =
OP1 + ⋯ + OPn
n
と書くことができます。GPはG不変ですから、その重心CもG不変であり、GはCを固定する合同変換群、すなわちCを中心とする回転から成る群です。Cを原点とする正規直交座標系をとれば、Gは直交群の部分群と考えることができます。
 平面の場合、GPは原点Cを中心とする半径CPの円周をn等分する点集合になり、O(2)を岩澤分解することにより、Gは 位数2nの正二面体群せいにめんたいぐん, dihedral groupDn
Dn := lc72 Rθ,  lb72
-1
0
0
1
rb72 Rθ mid72  θ =
2kπ
n
, k=0,⋯,n-1 rc72
Rθ := lb72
cos θ
-sin θ
sin θ
cos θ
rb72
の部分群となることがわかります。

定理2.2.3.3 平面の合同変換群の有限部分群

平面の合同変換群の有限部分群は、正二面体群の部分群である。

系2.2.3.4 正n角形の対称変換群

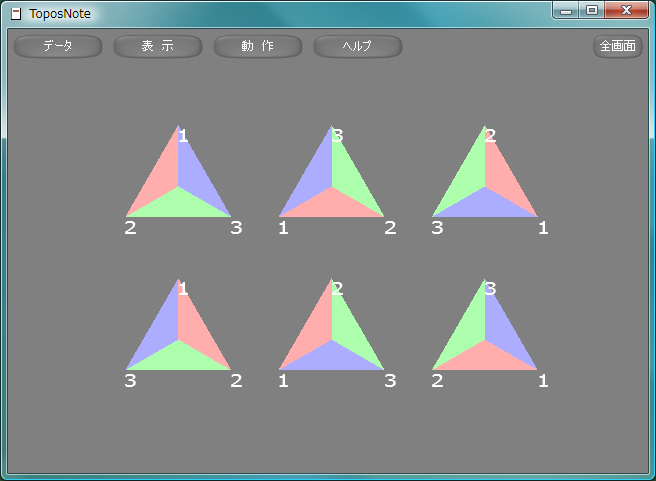
正n角形の対称変換群は、正二面体群Dnである。
2.2.4 正三角形の対称変換群
 正三角形の対称変換群D3 ≅ S3を図示します。
算譜2.2.4.2 sample201.lua
package.path = "std/?.lua"
require( "Geometry" )
 
a = ( math.sqrt( 3.0 ) / 2.0 ) * 0.8
vertices = {
  0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0,
  0.0, 0.0, 0.8, 0.0, 1.0, 0.0, 0.0, 0.0,
   -a, 0.0,-0.4, 0.0, 1.0, 0.0, 0.0, 0.0,
    a, 0.0,-0.4, 0.0, 1.0, 0.0, 0.0, 0.0
}
function triangle()
  dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
  dxSetColorHSV(   0.0, 0.5, 1.0 )
  dxTriangleMesh( 4, vertices, 1, { 0, 1, 2 } )
  dxSetColorHSV( 120.0, 0.5, 1.0 )
  dxTriangleMesh( 4, vertices, 1, { 0, 2, 3 } )
  dxSetColorHSV( 240.0, 0.5, 1.0 )
  dxTriangleMesh( 4, vertices, 1, { 0, 3, 1 } )
  dxPrint(  -0.0, 0.0, 0.8, 1.0, 1.0, 1.0, "1" )
  dxPrint(-a-0.0, 0.0,-0.4, 1.0, 1.0, 1.0, "2" )
  dxPrint( a+0.0, 0.0,-0.4, 1.0, 1.0, 1.0, "3" )
  dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
Triangle = Figure.new( function()
  triangle()
end )
E = Transformation.new( function()
end )
R1 = Transformation.new( function()
  RotateZ( 120.0 )
end )
R2 = Transformation.new( function()
  RotateY( 180.0 )
end )
T1 = Transformation.new( function()
  Translate( 2.0, 0.0, 0.0 )
end )
T2 = Transformation.new( function()
  Translate( 0.0,-2.0, 0.0 )
end )
 
draw =                         E * Triangle
draw =               ( T1 * R1 ) * Triangle
draw =           ( T1^2 * R1^2 ) * Triangle
draw =               ( T2 * R2 ) * Triangle
draw =     ( T1 * T2 * R1 * R2 ) * Triangle
draw = ( T1^2 * T2 * R1^2 * R2 ) * Triangle
 
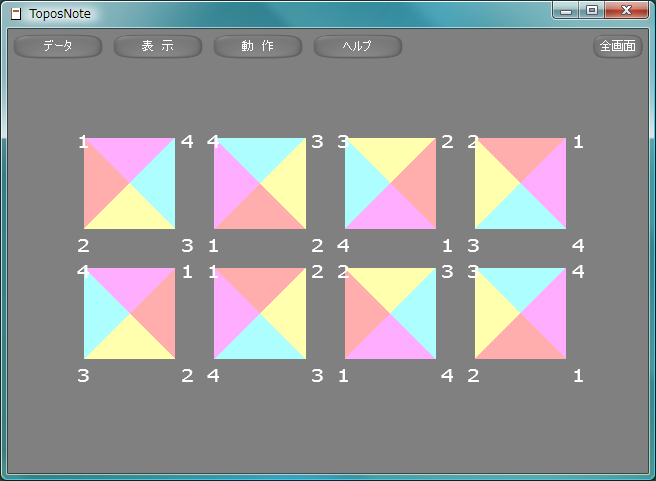
tnNewObject()
図2.2.4.3 sample201.lua
sample201.lua
2.2.5 正方形の対称変換群
 正方形の対称変換群D4を図示します。
算譜2.2.5.2 sample202.lua
package.path = "std/?.lua"
require( "Geometry" )
 
vertices = {
  0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0,
 -0.7, 0.0, 0.7, 0.0, 1.0, 0.0, 0.0, 0.0,
 -0.7, 0.0,-0.7, 0.0, 1.0, 0.0, 0.0, 0.0,
  0.7, 0.0,-0.7, 0.0, 1.0, 0.0, 0.0, 0.0,
  0.7, 0.0, 0.7, 0.0, 1.0, 0.0, 0.0, 0.0
}
function square()
  dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
  dxSetColorHSV(   0.0, 0.5, 1.0 )
  dxTriangleMesh( 5, vertices, 1, { 0, 1, 2 } )
  dxSetColorHSV(  90.0, 0.5, 1.0 )
  dxTriangleMesh( 5, vertices, 1, { 0, 2, 3 } )
  dxSetColorHSV( 180.0, 0.5, 1.0 )
  dxTriangleMesh( 5, vertices, 1, { 0, 3, 4 } )
  dxSetColorHSV( 270.0, 0.5, 1.0 )
  dxTriangleMesh( 5, vertices, 1, { 0, 4, 1 } )
  dxPrint( -0.8, 0.0, 0.8, 1.0, 1.0, 1.0, "1" )
  dxPrint( -0.8, 0.0,-0.8, 1.0, 1.0, 1.0, "2" )
  dxPrint(  0.8, 0.0,-0.8, 1.0, 1.0, 1.0, "3" )
  dxPrint(  0.8, 0.0, 0.8, 1.0, 1.0, 1.0, "4" )
  dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
Square = Figure.new( function()
  square()
end )
E = Transformation.new( function()
end )
R1 = Transformation.new( function()
  RotateZ( 90.0 )
end )
R2 = Transformation.new( function()
  RotateY( 180.0 )
end )
T1 = Transformation.new( function()
  Translate( 2.0, 0.0, 0.0 )
end )
T2 = Transformation.new( function()
  Translate( 0.0,-2.0, 0.0 )
end )
 
draw =                         E * Square
draw =               ( T1 * R1 ) * Square
draw =           ( T1^2 * R1^2 ) * Square
draw =           ( T1^3 * R1^3 ) * Square
draw =               ( T2 * R2 ) * Square
draw =     ( T1 * T2 * R1 * R2 ) * Square
draw = ( T1^2 * T2 * R1^2 * R2 ) * Square
draw = ( T1^3 * T2 * R1^3 * R2 ) * Square
 
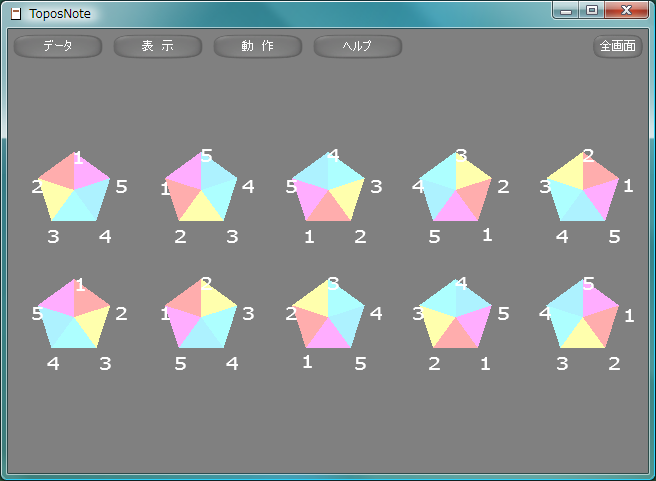
tnNewObject()
図2.2.5.3 sample202.lua
sample202.lua
2.2.6 正五角形の対称変換群
 正五角形の対称変換群D5を図示します。
算譜2.2.6.2 sample203.lua
package.path = "std/?.lua"
require( "Geometry" )
 
vertices = {
  0.0,    0.0, 0.0,    0.0, 1.0, 0.0, 0.0, 0.0,
  0.0,    0.0, 0.6,    0.0, 1.0, 0.0, 0.0, 0.0,
 -0.5706, 0.0, 0.1854, 0.0, 1.0, 0.0, 0.0, 0.0,
 -0.3527, 0.0,-0.4854, 0.0, 1.0, 0.0, 0.0, 0.0,
  0.3527, 0.0,-0.4854, 0.0, 1.0, 0.0, 0.0, 0.0,
  0.5706, 0.0, 0.1854, 0.0, 1.0, 0.0, 0.0, 0.0
}
function pentagon()
  dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
  dxSetColorHSV(   0.0, 0.5, 1.0 )
  dxTriangleMesh( 6, vertices, 1, { 0, 1, 2 } )
  dxSetColorHSV(  72.0, 0.5, 1.0 )
  dxTriangleMesh( 6, vertices, 1, { 0, 2, 3 } )
  dxSetColorHSV( 154.0, 0.5, 1.0 )
  dxTriangleMesh( 6, vertices, 1, { 0, 3, 4 } )
  dxSetColorHSV( 216.0, 0.5, 1.0 )
  dxTriangleMesh( 6, vertices, 1, { 0, 4, 5 } )
  dxSetColorHSV( 288.0, 0.5, 1.0 )
  dxTriangleMesh( 6, vertices, 1, { 0, 5, 1 } )
  dxPrint( -0.02,   0.0, 0.68,   1.0, 1.0, 1.0, "1" )
  dxPrint( -0.6657, 0.0, 0.2163, 1.0, 1.0, 1.0, "2" )
  dxPrint( -0.4114, 0.0,-0.5663, 1.0, 1.0, 1.0, "3" )
  dxPrint(  0.4114, 0.0,-0.5663, 1.0, 1.0, 1.0, "4" )
  dxPrint(  0.6657, 0.0, 0.2163, 1.0, 1.0, 1.0, "5" )
  dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
Pentagon = Figure.new( function()
  pentagon()
end )
E = Transformation.new( function()
end )
R1 = Transformation.new( function()
  RotateZ( 72.0 )
end )
R2 = Transformation.new( function()
  RotateY( 180.0 )
end )
T1 = Transformation.new( function()
  Translate( 2.0, 0.0, 0.0 )
end )
T2 = Transformation.new( function()
  Translate( 0.0,-2.0, 0.0 )
end )
 
draw =                         E * Pentagon
draw =               ( T1 * R1 ) * Pentagon
draw =           ( T1^2 * R1^2 ) * Pentagon
draw =           ( T1^3 * R1^3 ) * Pentagon
draw =           ( T1^4 * R1^4 ) * Pentagon
draw =               ( T2 * R2 ) * Pentagon
draw =     ( T1 * T2 * R1 * R2 ) * Pentagon
draw = ( T1^2 * T2 * R1^2 * R2 ) * Pentagon
draw = ( T1^3 * T2 * R1^3 * R2 ) * Pentagon
draw = ( T1^4 * T2 * R1^4 * R2 ) * Pentagon
 
tnNewObject()
図2.2.6.3 sample203.lua
sample203.lua
2.2.7 参考文献
[1] 梅谷 武, 幾何学事始, pisan-dub.jp, 2009
[2] H.S.M. コクセター, 幾何学入門(上), ちくま学芸文庫, 2009
img
 
 
[3] H.S.M. コクセター, 幾何学入門(下), ちくま学芸文庫, 2009
img
 
 
[4] Elmer G. Rees, 幾何学講義, 共立出版, 1992
img
 
 
[5] 志賀 浩二, 群論への30講, 朝倉書店, 1989
img
 
 
[6] 原田 耕一郎, 群の発見, 岩波書店, 2001
img
 
 
数　　学
対称性 たいしょうせい, symmmetry
対称変換群 たいしょうへんかんぐん, symmetry transformation group
置換 ちかん, permutation
対称群 たいしょうぐん, symmetric group
位数 いすう, order
互換 ごかん, transposition
偶置換 ぐうちかん, even permutation
奇置換 きちかん, odd permutation
符号 ふごう, signature
交代群 こうたいぐん, alternating group
正二面体群 せいにめんたいぐん, dihedral group
 
Published by SANENSYA Co.,Ltd.