1.1節 正多角形
著者:梅谷 武
語句:定規とコンパスによる作図法, フェルマー素数, 1のn乗根
原論における正多角形の取り扱いについて述べる。
作成:2010-01-07
更新:2021-07-01
原論においては正三角形、正方形、正五角形、正六角形、正十五角形の作図法が与えられています。これらはすべて与えられた円に内接させることができます。
与えられた直線を一辺とする正三角形を作図すること。
与えられた等辺で等角な五角形に円を内接させること。
与えられた円に等辺で等角な六角形を内接させること。
与えられた円に等辺で等角な十五角形を内接させること。
命題I-9「与えられた角を二等分すること。」より、正q角形が作図できれば、正2k q角形も作図できますから、正n角形の作図可能性を論ずるときにnとして素因数分解が奇素数だけから成るものだけを考えてかまいません。
原論では
p = 3, 5という素数に対して、正
p角形の作図法を与えていますが、その後、それ以外の素数
pに対する正
p角形の作図法が与えられるのは近代になってからです。
高木貞治たかぎ ていじ, 1875-1960『近世数学史談』の冒頭に、
ガウスGauss, Johann Carl Friedrich, 1777-1855が正十七角形の作図法を発見したときの様子が描かれています。
1796年3月30日の朝、十九歳の青年ガウスが目ざめて臥床から置き出でようとする刹那に正十七角形の作図法に思い付いた。
──高木貞治『近世数学史談』より
この発見の意義について、
クラインKlein, Felix Christian, 1849-1925が『19世紀の数学』で簡潔に説明しています。
期せずしてこれを発見したとき、ガウスはまだ19歳に満たなかったが、これによって、二千年来発展のなかった正多角形の作図問題は一挙に大きく前進した、というか、最終的な決着がついた、というのも、彼はまもなく、任意の正多角形の作図可能性は
nの数論的性質にのみ依存することを見抜き、その判定条件を与えることに成功したからである。たとえば、
nが素数のときには
の形でなければならないというのである。
──クライン『19世紀の数学』より
この形の素数はフェルマー素数
Fkと呼ばれ、現在まで知られているものは次の五つです。
ガウスはnの奇素因数がフェルマー素数のときにだけ、定規とコンパスで作図できることを示しました。このことから正七角形や正九角形は作図できないことがわかります。
近年、折り紙による作図法の研究が進み、角の三等分や正七角形・正九角形等の作図法が発表されており、定規とコンパスによる作図法を拡張する試みとして注目されています。[
4]
原論における定規とコンパスによる作図法は、あくまでも数学の理論体系を構築することを目的としており、当時においても建築や工芸の現場では原論の作図法がそのまま使われることはなかったでしょう。
現代において一般的に作図といえば、CGやCADにより数値的に図形を定義することを指していると考えてかまいません。計算機は有理数しか扱うことができませんが、必要な精度の近似を使うことでどんな図形でも描くことができます。現代の作図法は、実数論上に構築された幾何学や解析学に基づくものですが、原論の立場からは正n角形を必要なだけ近似する方法を与えていると解釈することができます。
正
n角形を描くことは円を
n等分することと同じですから、角度を弧度法で表わすとすれば、X-Y平面上に半径
1の円を描いたとき、円周上の
n個の点
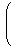 cos cos | | , sin | | 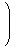 ,
k = 0, ⋯, n-1 ,
k = 0, ⋯, n-1
|
は円を
n等分しています。複素平面上の場合は
| cos | | + i sin | | ,
k = 0, ⋯, n-1
|
と極形式で表現できて、代数方程式
Xn - 1の解、すなわち1のn乗根になっています。
人 物
高木貞治 たかぎ ていじ, 1875-1960
ガウス Gauss, Johann Carl Friedrich, 1777-1855
クライン Klein, Felix Christian, 1849-1925
アルブレヒト・デューラー Dürer, Albrecht, 1471-1528



