7.5節 Lie環
著者:梅谷 武
語句:Lie環, 交代行列, 反エルミート行列, 世界座標系, 物体座標系, 速度ベクトル, 接ベクトル, 随伴表現
線形Lie群のLie環の概念を導入し、三次元単位球面による直交群の被覆がSU(2)の随伴表現と同じものであることを示す。
作成:2009-09-26
更新:2021-03-28
解析的な議論を最小限にするために行列値関数の微分について必要な性質だけまとめます。
証明
略■
形式的冪級数
に行列
X ∈ M(n,K)を代入すると行列のノルムに関して絶対収束することから、行列の指数関数
exp:M(n,K)  GL(n,K), X GL(n,K), X  exp X := eX exp X := eX
|
を定義することができます。
行列の指数関数について次が成り立つ。
| (1)
| | XY = YX ⇒ eX+Y=eX eY, X,Y ∈ M(n,K)
|
|
| (2)
| | (eX)n = enX, X ∈ M(n,K), n ∈ ℤ
|
|
| (3)
| | ePXP-1 = P eX P-1, X ∈ M(n,K), P ∈ GL(n,K)
|
|
| (4)
| |
| (5)
| |
| (6)
| |
| (7)
| | det(eX) = eTr(X), X ∈ M(n,K)
|
|
| (8)
| | (etX) = X etX = etX X, X ∈ M(n,K), t ∈ ℝ
|
|
証明
略■
最初に代数構造としてのLie環を定義します。
K上の線形空間
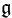
において、積
が定義され、次の条件が満たされるとき、
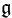
を
K上の
Lie環りーかん, Lie algebraという。
| (LA1)
| [X+Y,Z] = [X,Z] + [Y,Z], X,Y,Z ∈ 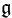 |
| (LA2)
| [λ X,Y] = λ [X,Y], λ ∈ K, X,Y ∈ 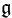 |
| (LA3)
| [X,Y] = -[Y,X], X,Y ∈ 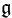 |
| (LA4)
| [X,[Y,Z]] + [Y,[Z,X]] + [Z,[X,Y]], X,Y,Z ∈ 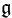 |
次に線形Lie群のLie環を定義します。
線形Lie群
G ⊂ GL(n,K)について、
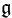 := { X ∈ M(n,K) ∣ etX ∈ G, t ∈ ℝ } := { X ∈ M(n,K) ∣ etX ∈ G, t ∈ ℝ }
|
を線形Lie群
GのLie環という。
線形Lie群
GのLie環
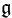
は積
| [X,Y] := XY - YX, X,Y ∈ M(n,K)
|
により、実数体
ℝ上のLie環となる。
証明
略■
線形Lie群
GのLie環は対応するドイツ小文字
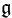
で表すことにします。
証明
略■
| (7.5) | 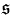 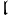 (n,ℝ) =
{ X ∈ M(n,ℝ) ∣ Tr(X) = 0 } (n,ℝ) =
{ X ∈ M(n,ℝ) ∣ Tr(X) = 0 }
|
|
| (7.6) | 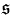 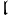 (n,ℂ) =
{ X ∈ M(n,ℂ) ∣ Tr(X) = 0 } (n,ℂ) =
{ X ∈ M(n,ℂ) ∣ Tr(X) = 0 }
|
|
証明
| det(etX) = et Tr(X) = 1 ⇔
Tr(X) = 0
|
■
| (7.7) | 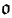 (n) = (n) = 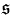 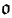 (n) =
{ X ∈ M(n,ℝ) ∣ tX + X = 0 } (n) =
{ X ∈ M(n,ℝ) ∣ tX + X = 0 }
|
|
証明
| t(etX)(etX) = et(tX + X) = En ⇔ tX + X = 0
|
■
| (7.8) | 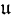 (n) = { X ∈ M(n,ℂ) ∣ X† + X = 0 } (n) = { X ∈ M(n,ℂ) ∣ X† + X = 0 }
|
|
証明
| (etX)†(etX) = et(X† + X) = En ⇔
X† + X = 0
|
■
| (7.9) | 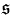 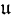 (n) =
{ X ∈ M(n,ℂ) ∣ X† + X = 0,
Tr(X) = 0 } (n) =
{ X ∈ M(n,ℂ) ∣ X† + X = 0,
Tr(X) = 0 }
|
|
証明
略■
物体座標系に固定されている物体の運動は物体座標系の時間変化によって記述することができます。(o1,o2,o3)は世界座標系で表現すると(3,3)特殊直交行列と考えることができますから、物体の運動は時間量から運動群ℝ3 ⋊ SO(3)への写像で表現することができます。以後、時間量は線長量と同型であると仮定し、時間の単位を定めることによって実数ℝと同一視することにしましょう。
原点を固定する物体の運動
R(t)R : ℝ  SO(3), t SO(3), t  R(t) R(t)
|
について考えます。常に
が成り立っています。
時刻
0において世界座標系と物体座標系が一致すると仮定しましょう。これは次のように表現されます。
R(t)の直交性を表す式を微分すると
| tR(t)R(t) + tR(t)R(t) = 0
|
となることから
R(0) = E3を代入すると、
t = 0における接ベクトルは、
より、交代行列となります。逆に任意の交代行列
Xについて
R(t) := etXとおくと
となり、
SO(3)の単位元
E3における接ベクトル空間とLie環
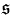
 (3)
(3)は一致することがわかります。
線形Lie群のLie環とは、線形Lie群の単位元における接ベクトル空間に他なりません。
SO(3)のLie環
 (3)
(3)の構造を調べてみましょう。
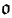 (3)
(3)の元は交代行列ですから、対角成分は
0であり、交代性から成分の決め方の自由度は三つしかありません。したがって、
J1,J2,J3 ∈ 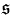
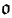 (3)
(3)を
と定めると、これらは
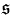
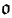 (3)
(3)の基底となり、
と表すことができます。回転のオイラー角表現行列を
Rn(t), n = 1,2,3とすると
| (7.12) | | etJn = Rn(t), n = 1,2,3, t ∈ ℝ
|
|
が成り立っています。
SU(2)のLie環
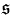
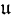 (2)
(2)の構造を調べてみましょう。
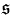
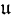 (2)
(2)の元は反エルミート行列ですから、
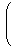 | | 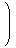 |
∈ Mat(Im ℍ)
|
という形をしています。これは空間
Im ℍの行列表現であり、基底
により
| (7.16) | | Mat(Im ℍ) =
ℝ I ⊕ ℝ J ⊕ ℝ K
|
|
と直和表現されます。
X ∈ 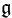
ならば
etX ∈ Gですから、
より
Ad(g)X ∈ 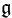
であり、
| Ad(gh) = Ad(g)Ad(h),
Ad(g-1) = Ad(g)-1
|
が成り立つことから、
Adは
Gから
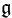
上の一般線形群への準同型であることがわかります。
SU(2)は三次元単位球面
S3の行列表現であることから、全射群準同型
φ:S3  SO(Im ℍ),
a SO(Im ℍ),
a  φa,a φa,a
|
は
Ad : SU(2)  SO(Im ℍ),
g SO(Im ℍ),
g  Ad(g) Ad(g)
|
と同じものであり、次の定理が成り立ちます。
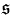
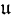 (2) = Mat(Im ℍ)
(2) = Mat(Im ℍ)であり、
SU(2)の
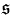
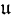 (2)
(2)上への随伴表現は全射準同型
Ad : SU(2)  SO(3) SO(3)
|
を引き起こし、その核は
{E2,-E2}であり、次の群同型を誘導する。
[
2] 江沢 洋, 島 和久,
群と表現, 岩波書店, 2009
数 学
Lie環 りーかん, Lie algebra
交代行列 こうたいぎょうれつ, alternative matrix
反エルミート行列 はんえるみーとぎょうれつ, skew-Hermitian matrix
世界座標系 せかいざひょうけい, world coordinate system
物体座標系 ぶったいざひょうけい, object coordinate system
速度ベクトル そくどべくとる, velocity vector
接ベクトル せつべくとる, tangent vector
随伴表現 ずいはんひょうげん, adjoint representation
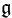 で表すことにします。
で表すことにします。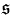
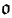 (3)は一致することがわかります。
(3)は一致することがわかります。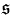
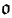 (3)の構造を調べてみましょう。
(3)の構造を調べてみましょう。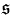
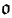 (3)の元は交代行列ですから、対角成分は0であり、交代性から成分の決め方の自由度は三つしかありません。したがって、J1,J2,J3 ∈
(3)の元は交代行列ですから、対角成分は0であり、交代性から成分の決め方の自由度は三つしかありません。したがって、J1,J2,J3 ∈ 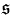
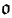 (3)を
(3)を
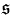
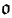 (3)の基底となり、
(3)の基底となり、
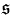
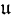 (2)の構造を調べてみましょう。
(2)の構造を調べてみましょう。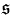
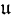 (2)の元は反エルミート行列ですから、
(2)の元は反エルミート行列ですから、
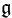 に対して次のように左から作用します。
に対して次のように左から作用します。
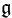 上への随伴表現ずいはんひょうげん, adjoint representationといいます。
上への随伴表現ずいはんひょうげん, adjoint representationといいます。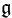 ならばetX ∈ Gですから、
ならばetX ∈ Gですから、
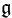 であり、
であり、
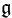 上の一般線形群への準同型であることがわかります。
上の一般線形群への準同型であることがわかります。

