7.3節 空間比例としての四元数
著者:梅谷 武
語句:三次元単位球面, シンプレクティック群
四元数の単位球面が特殊ユニタリ群SU(2)と同型であり、回転群SO(3)を二重被覆することを示す。これにより、四元数論が空間比例論であると結論される。
作成:2009-09-25
更新:2021-03-28
Mat(ℍ)の元
Aについて
AA†を計算してみましょう。
となり、行列式が
1の
Mat(ℍ)の元
Aはユニタリ行列であることがわかります。逆に
SU(2)の元
Aについて
とすると、逆行列は
| A-1 =
| 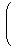 | | 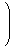 |
|
なので、
d = a, c = -bであり、
| A =
| 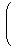 | | 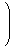 |
|
と書くことができます。ですから
Aは
Mat(ℍ)の元になっています。
| (7.1) | | SU(2) = { A ∈ Mat(ℍ) ∣ det A = 1 }
|
|
このことによって、次の定理が証明できました。
Mat:ℍ → Mat(ℍ)は
S3と
SU(2)の群(さらにはLie群)としての同型を与える。
四元数
a = a0 e + a1 i + a2 j + a3 kについて
Mat(a)の行列式を計算してみます。
| | | (a0 + a1 i)(a0 - a1 i) + (a2 + a3 i)(a2 - a3 i) |
|
| | |
したがって、次の命題が成り立ちます。
四元数
ℍ上の直交群は内積を保存する線形変換のなす群
O(ℍ)として定義されます。これは行列表現すると
| | | { A ∈ GL(4,ℝ) | tA A = A tA = E4 } |
|
| | |
| | |
| | | { A ∈ O(ℍ) ∣ det A = -1 } |
|
となり、これまでと同じようですが、四元数
ℍ上に積が定義されていることにより、通常の線形群とは異なる様相を示します。
a,b ∈ S3とするとき、
φa,b:ℍ  ℍ,
x ℍ,
x  axb axb
|
φa,b:ℍ  ℍ,
x ℍ,
x  axb axb
|
は、ノルムを保存する線形変換ですから直交変換になります。逆にすべての四元数
ℍ上の直交変換はこれで尽くされています。
四元数
ℍ上の直交変換について次が成り立つ。
| (1)
| O+(ℍ)の任意の元はa,b ∈ S3によって
φa,bと書ける。
|
| (2)
| O-(ℍ)の任意の元はa,b ∈ S3によって
φa,bと書ける。
|
証明
略■
空間に付随するベクトル空間
Im ℍ上の直交変換
Aは直交直和分解
により、
| A'
:=
| 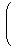 | | 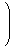 |
|
と一意的に拡張することができます。
A' ∈ O+(ℍ)であれば、
a,b ∈ S3が存在して、直交変換として
A' = φa,bが成り立ちますから、
A'(e)=eより、
| aeb = ab = e ⇒ b = a-1 = a
|
となり、
A' = φa,aと書くことができます。
A' ∈ O-(ℍ)のときは
-A' ∈ O+(ℍ)ですから、
A' = -φa,aと書くことができます。
これにより次の定理が成り立つことがわかりました。
空間に付随するベクトル空間
Im ℍ上の直交変換について次が成り立つ。
| (1)
| O+(Im ℍ)の任意の元はa ∈ S3によって
φa,aと書ける。
|
| (2)
| O-(Im ℍ)の任意の元はa ∈ S3によって
-φa,aと書ける。
|
三次元単位球面
S3から回転群
SO(Im ℍ)への写像
φ:S3  SO(Im ℍ),
a SO(Im ℍ),
a  φa,a φa,a
|
について考えます。
まず、
x ∈ Im ℍについて
x = -xが成り立つので、
| (a x a)- =
a x a
= - a x a
|
より、
axa ∈ Im ℍであり、
φa,a ∈ SO(Im ℍ)がわかります。
a,b ∈ S3について、
| φa,a ∘ φb,b(x)
= a b x b a
= a b x ab
= φab,ab
|
より、
φは群準同型になっています。また、前小節の結果からこれは全射です。
a ∈ S3について、
φa,aが恒等写像であるとすると
が任意の
x ∈ Im ℍについて成り立ちますから、特に
i,j,kについて成り立ち、
a ∈ ℝeであり、
a = ± eであることがわかります。
三次元単位球面
S3から回転群
SO(Im ℍ)への写像
φ:S3  SO(Im ℍ),
a SO(Im ℍ),
a  φa,a φa,a
|
は群の全射準同型であり、その核は
{e,-e}となる。これにより群同型
が誘導される。さらにこれはLie群としての同型を与えている。
証明
略■
実際に
axaを計算してみましょう。
| a = a0 e + a1 i + a2 j + a3 k ∈ S3,
x = x1 i + x2 j + x3 k ∈ Im ℍ
|
とすると
| | | (a0e + Im(a))x(a0e - Im(a)) |
|
| | | (a0e + Im(a))
( 〈 x, Im(a) 〉 e
+ a0x - x × Im(a) ) |
|
| | | ( a0 〈 x, Im(a) 〉
- 〈 Im(a), a0x - x × Im(a) 〉 ) e |
|
| | | + a02 x - a0x × Im(a)
+ 〈 Im(a), x 〉 Im(a) |
|
| | | - a0x × Im(a)
- Im(a) × (x × Im(a)) |
|
ここで、実部はすでに
0になることがわかっていますが計算しても
0になります。虚部をベクトル積の公式
| a × (b × c)
= 〈a,c〉b - 〈a,b〉c
|
を使って展開・整理すると次が得られます。
| (7.4) | | axa =
(2a02 - 1)x + 2〈 Im(a),
x 〉 Im(a)
+ 2a0 Im(a) × x
|
|
この各項を
(3,3)行列で表現します。
これらをまとめます。
a = a0 e + a1 i + a2 j + a3 k ∈ S3について
φa,a ∈ SO(Im ℍ)の行列表現は次のようになる。
0でない四元数
ℍ×は
ℝ+ × S3と同一視することができますから、この結果から
であることがわかり、この意味で四元数は立体図形の向きを保存する相似変換であるということができます。これにより、四元数論とは空間比例論であるという結論に到達できました。
[
1] L.S.ポントリャーギン,
数概念の拡張, 森北出版, 1995
[
2] H.D.エビングハウス,
数 (上), シュプリンガー・フェアラーク東京, 1991
[
3] H.D.エビングハウス,
数 (下), シュプリンガー・フェアラーク東京, 1991
数 学
三次元単位球面 さんじげんたんいきゅうめん,
3 dimensional unit sphere
シンプレクティック群 しんぷれくてぃっくぐん,
symplectic group


