6.6節 運動幾何
著者:梅谷 武
語句:回転群, 運動群, 部分空間, 直交補空間, オイラー角, ジンバルロック, ヨー, ピッチ, ロール
空間の運動群の構造を決定し、オイラー角による回転の表現について述べる。
作成:2009-09-17
更新:2021-03-28
6.6 運動幾何
6.6.1 回転と鏡映
 行列式detを直交群O(3)から乗法群ℝ×への群準同型写像と考えます。
det : O(3) longrightarrow ℝ×,  A longmapsto det A
直交群の元Aは合同変換ですから、特に等積変換です。したがってdet A = 1であり、その像は
det (O(3)) = {1,-1}
という離散集合になります。この写像の核は回転群
SO(3) := { A ∈ GL(3,ℝ) | tA A = A tA = E3, det A = 1 }
となり、直交群は次のように剰余類に分解されます。
O(3) = SO(3) ∪ lb96
-1
0
0
0
1
0
0
0
1
rb96 SO(3)
後にSO(3)が弧状連結であり、直交群の単位元を含む連結成分であることが示されます。この分解に出てくる鏡映変換によって生成される位数2の鏡映群をRef(3)と書くことにすれば、直交群は鏡映群と回転群の直積に分解することができます。

定理6.6.1.2 直交群の構造

直交群O(3)は鏡映群Ref(3)と回転群SO(3)の直積である。
O(3) ≅ Ref(3) × SO(3)
6.6.2 回転の軸
 空間(U,V3)において正規直交座標系(O,e1,e2,e3)を固定して考えます。
 回転群SO(3)の任意の元Aについて、
          det (A - E3)
=
det t(A - E3) = det (tA - E3)
=
det (A-1 - E3) = det A-1 det (E3 - A)
=
det (- E3) det (A - E3) = - det (A - E3)
より、
det (A - E3) = 0
つまり、A - E3は正則ではありませんから、
A x = x
となる0でないベクトルx ∈ V3が存在します。
e1' :=
x
x
とおくとA e1' = e1'が成り立ちます。
 線形空間V3において、その部分集合で線形空間になっているものを部分空間ぶぶんくうかん, subspaceと呼びます。V3の任意の部分集合Vに対して
V⊥ := { x ∈ V3 ∣ 〈 x, v 〉 = 0,  v ∈ V }
とおくと、V⊥はV3の部分空間になっています。これをVの直交補空間ちょっこうほくうかん, orthogonal complementと呼びます。
 e1'が生成する部分空間をV := ℝ e1'とすると、
V3 = V ⊕ V⊥
と直和分解できます。直和分解とは任意の元x ∈ V3が、
x = v + w, v ∈ V, w ∈ V⊥
と一意的に分解できることをいいます。このとき回転Aも
A x = A v + A w,  A V ⊂ V,  A V⊥ ⊂ V⊥
と分解されます。
 V⊥はe1'に属する有向線分に直交する平面上にある有向線分 の同値類ですから、その平面上のベクトルe2',e3'を選んで、 (e1',e2',e3')が正規直交基底となるようにすることができます。 このとき、Aを新しい座標系で表現すると、
lb96
1
0
0
0
a11
a12
0
a21
a22
rb96
となります。ここで、
1
0
0
0
a11
a12
0
a21
a22
 =
a11
a12
a21
a22
 = 1
より、AのV⊥への制限はSO(2)の元であり、結局Aはθ ∈ [0,4∠R)によって
R1(θ) := lb96
1
0
0
0
cos θ
-sin θ
0
sin θ
cos θ
rb96
と表現されることがわかります。つまり、Aはe1'を軸とする二次元的な回転になっています。
6.6.3 オイラー角
 空間(U,V3)において正規直交座標系(O,e1,e2,e3)を固定し、回転群SO(3)の任意の元Aについて、
e1' := A e1, e2' := A e2, e3' := A e3
と置きます。e3'がe3となす角をθ ∈ [0,2∠R]とします。
 θ = 0のとき、Aはe3を軸とする回転ですから、
A = R3(ψ) := lb96
cos ψ
-sin ψ
0
sin ψ
cos ψ
0
0
0
1
rb96,  ψ ∈ [0,4∠R)
と書くことができます。
 0 ＜ θ ＜ 2∠Rのとき、e3'をe3を軸とする負方向の回転によってe2,e3が生成する平面上、e2の負方向に写します。
e' := R3(-ψ) e3',  ψ ∈ [0,4∠R)
さらに、e'をe1を軸とする負方向の回転によってe3に一致させます。
e3 = R1(-θ) e',  ψ ∈ [0,4∠R)
これにより、
e3 = R1(-θ) S3(-ψ) A e3
が成り立ち、R1(-θ) R3(-ψ) Aはe3を軸とする回転であることがわかります。したがって、
R1(-θ) R3(-ψ) A = R3(φ),  φ ∈ [0,4∠R)
と書くことができ、
A = R3(ψ) R1(θ) R3(φ)
が成り立ちます。
 θ = 2∠Rのとき、上でψ = 0と考えると
A = R1(2∠R) R3(φ) = R3(φ)
が成り立ちます。
 結局、次の定理が証明できました。

定理6.6.3.6 回転のオイラー角表現

回転群SO(3)の任意の元Aは、
     A
=
R3(ψ) R1(θ) R3(φ)
=
lb96
cos ψ
-sin ψ
0
sin ψ
cos ψ
0
0
0
1
rb96 lb96
1
0
0
0
cos θ
-sin θ
0
sin θ
cos θ
rb96 lb96
cos φ
-sin φ
0
sin φ
cos φ
0
0
0
1
rb96
θ ∈ [0,2∠R], ψ, φ ∈ [0,4∠R)
と表現することができる。このときの角度の組(ψ, θ, φ)をオイラー角おいらーかく, Euler's anglesと呼ぶ。
 オイラー角表現の行列の積を計算しておきます。
R3(ψ) R1(θ) R3(φ)
=
lb96
cos ψ
-sin ψ
0
sin ψ
cos ψ
0
0
0
1
rb96 lb96
1
0
0
0
cos θ
-sin θ
0
sin θ
cos θ
rb96 lb96
cos φ
-sin φ
0
sin φ
cos φ
0
0
0
1
rb96
=
lb96
cosψcosφ-sinψcosθsinφ
-cosψsinφ-sinψcosθcosφ
sinψsinθ
sinψcosφ+cosψcosθsinφ
-sinψsinφ+cosψcosθcosφ
-cosψsinθ
sinθsinφ
sinθcosφ
cosθ
rb96
 ここでθ = 0もしくはθ = 2∠Rを代入すると
lb96
cos ψ cos φ - sin ψ sin φ
-cos ψ sin φ - sin ψ cos φ
0
sin ψ cos φ + cos ψ sin φ
-sin ψ sin φ + cos ψ cos φ
0
0
0
1
rb96
=
lb96
cos(ψ + φ)
-sin(ψ + φ)
0
sin(ψ + φ)
cos(ψ + φ)
0
0
0
1
rb96
となり、ψとφにどんな値を代入しても、第3軸の回転にしかなりません。これが慣性航法システムにおけるジンバルロックじんばるろっく, gimbal lockと呼ばれる現象の数学的な意味です。オイラー角表現は一意的ではなく、回転軸の選び方はさまざまですが、どの場合においてもこのような特異点が存在します。これはオイラー角表現が特異点の近傍でSO(3)と局所同相になっていないことが原因です。後にSU(2)からSO(3)への被覆写像により、特異点を持たない回転の表現を与えます。SU(2)の元は絶対値が1の四元数と同じものです。
6.6.4 運動群
 オイラー角表現は連続写像
[0,4∠R) × [0,2∠R] × [0,4∠R) longrightarrow SO(3)
(ψ, θ, φ) longmapsto R3(ψ) R1(θ) R3(φ)
を定めますが、これは全射で、弧状連結領域の連続像は弧状連結になることからSO(3)は弧状連結であり、これにより空間の運動群が決定されました。

定理6.6.4.2 運動群の構造

空間における運動群Motion(U)は、平行移動群Trans(U)に内部自己同型によって回転群SO(V3)を作用させた半直積に同型である。
Motion(U) ≅ Trans(U) ⋊ SO(V3)
6.6.5 ヨー・ピッチ・ロール
 オイラー角表現は特異点により、ジンバルロックのような障害が発生する可能性があるものの、回転の表現法としては実用上重要な役割を担っています。ここでは、飛行機等の姿勢制御で使われるヨー・ピッチ・ロールによる表現について、ゲーム用CGデータ標準であるCOLLADA形式やそれを採用している地理情報マークアップ言語KMLに準拠し、リファレンスとして使えるように整理しておきます。
 ヨーよー, yawとは機首を左右に振る動きを表し、ピッチぴっち, pitchとは機首を上下に振る動きを表し、ロールろーる, rollとは機体を軸に左右に回転する動きを表します。
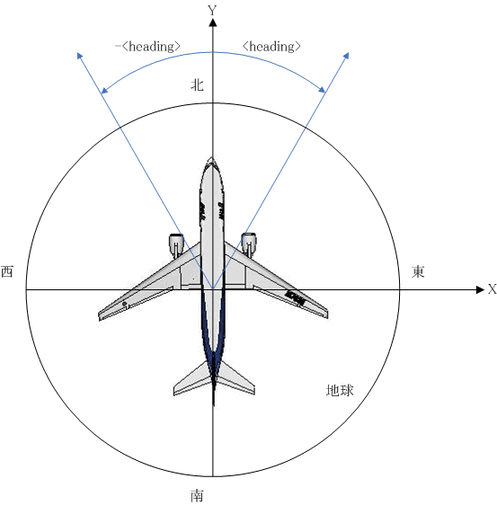
図6.6.5.3 ヨー(yaw,heading)：方位角
ヨー(yaw,heading)：方位角
 ヨーは「heading」というタグで表され、その値ψは負方向の角度で範囲は-180 ＜ ψ ＜ 180[度]、規定値は0です。
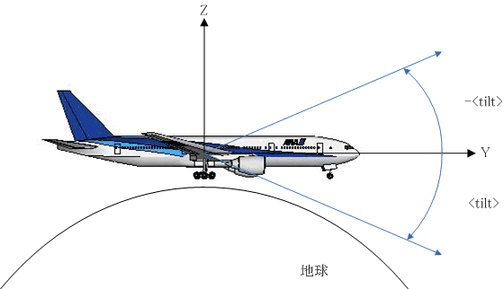
図6.6.5.5 ピッチ(pitch,tilt)：仰角
ピッチ(pitch,tilt)：仰角
 ピッチは「tilt」というタグで表され、その値θの負方向の角度で範囲は-90 ＜ θ ＜ 90[度]、規定値は0です。
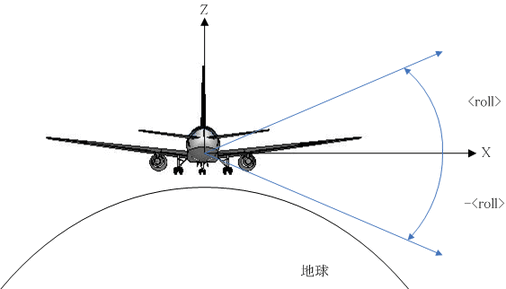
図6.6.5.7 ロール(roll)：傾斜角
ロール(roll)：傾斜角
 ロールは「roll」というタグで表され、その値φの負方向の角度で 範囲は-180 ＜ φ ＜ 180[度]、規定値は0です。
 座標軸は右手系のX-Y-Zで表現され、地球表面上の極点以外の点における局所座標系を表しており、X-Y平面が水平面、Z軸が鉛直方向の上方向、Y軸は北方向、X軸は東方向に対応しています。
 変換はヨー・ピッチ・ロールの順に行われます。CGモデルを仮想空間に配置する場合にはこの順番がもっとも人間の感覚に合っていますが、他の用途では必ずしもこの順番がいいとは限りません。
RY(φ) RX(θ) RZ(ψ)
=
lb96
cos φ
0
sin φ
0
1
0
-sin φ
0
cos φ
rb96 lb96
1
0
0
0
cos θ
-sin θ
0
sin θ
cos θ
rb96 lb96
cos ψ
-sin ψ
0
sin ψ
cos ψ
0
0
0
1
rb96
=
lb96
cosφcosψ+sinφsinθsinψ
-cosφsinψ+sinφsinθcosψ
sinφcosθ
cosθsinψ
cosθcosψ
-sinθ
-sinφcosψ+cosφsinθsinψ
sinφsinψ+cosφsinθcosψ
cosφcosθ
rb96
この式を利用する場合は、COLLADA形式では角度の方向が負であることに注意してください。データ値の符号を反転し、弧度法に変換する前処理が必要です。
6.6.6 参考文献
[1] 山内 恭彦, 杉浦 光夫, 連続群論入門, 培風館, 1960
[2] 横田 一郎, 群と位相, 裳華房, 1971
img
 
 
[3] 平井 武, 線形代数と群の表現(I), 朝倉書店, 2001
img
 
 
数　　学
部分空間 ぶぶんくうかん, subspace
直交補空間 ちょっこうほくうかん, orthogonal complement
オイラー角 おいらーかく, Euler's angles
ジンバルロック じんばるろっく, gimbal lock
ヨー よー, yaw
ピッチ ぴっち, pitch
ロール ろーる, roll
 
Published by SANENSYA Co.,Ltd.