6.3節 外積とベクトル積
著者:梅谷 武
語句:外積, ベクトル積, 法線ベクトル
空間に付随するベクトル空間上の外積とベクトル積を定義する。
作成:2009-09-16
更新:2011-03-08
空間内の二つのベクトル
a,bの外積
a ∧ bは平面ベクトルの外積を利用して定義します。正規直交座標系
(O;e1,e2,e3)により、二つのベクトル
a,bが次のように座標表現されているとします。
| a =
λ1 e1 + μ1 e2 + ξ1 e3
=
|  | |  |
|
| b =
λ2 e1 + μ2 e2 + ξ2 e3
=
|  | |  |
|
三つの基底ベクトルの二つから生成される座標平面を考えます。
二つのベクトル
a,bのこれらの座標平面への射影を次のように記します。
| a23 = μ1 e2 + ξ1 e3,
b23 = μ2 e2 + ξ2 e3
|
| a31 = ξ1 e3 + λ1 e1,
b31 = ξ2 e3 + λ2 e1
|
| a12 = λ1 e1 + μ1 e2,
b12 = λ2 e1 + μ2 e2
|
各座標平面への射影の外積を計算します。
| | |
| | | ( μ1 ξ2 - ξ1 μ2 ) e2 ∧ e3
∈ A23 := ℝ e2 ∧ e3 |
|
| | |
| | | ( ξ1 λ2 - λ1 ξ2 ) e3 ∧ e1
∈ A31 := ℝ e3 ∧ e1 |
|
| | |
| | | ( λ1 μ2 - μ1 λ2 ) e1 ∧ e2
∈ A12 := ℝ e1 ∧ e2 |
|
これらの面積量はそれぞれ意味が異なるので別の種類の量と考えます。そして空間ベクトルの外積を次のように定義します。
V3 × V3  A23 ⊕ A31 ⊕ A12,
(a,b)
A23 ⊕ A31 ⊕ A12,
(a,b)  a ∧ b a ∧ b
|
| a ∧ b :=
a23 ∧ b23 +
a31 ∧ b31 +
a12 ∧ b12
|
座標展開すると次のようになります。
| | | ( μ1 ξ2 - ξ1 μ2 ) e2 ∧ e3
+ ( ξ1 λ2 - λ1 ξ2 ) e3 ∧ e1
+ ( λ1 μ2 - μ1 λ2 ) e1 ∧ e2 |
|
| | |
e2 ∧ e3
-
| |
e3 ∧ e1
+
| |
e1 ∧ e2 |
|
空間に付随するベクトル空間
V3上の二つのベクトルの外積は双線形かつ交代である。すなわち、次が成り立つ。
| (EXT1)
| ( a + b ) ∧ c = a ∧ c + b ∧ c,
a,b,c ∈ V3
|
| (EXT2)
| a ∧ ( b + c ) = a ∧ b + a ∧ c,
a,b,c ∈ V3
|
| (EXT3)
| λ a ∧ b = λ a ∧ b = a ∧ λ b,
a,b ∈ V3, λ ∈ ℝ
|
| (EXT4)
| a ∧ a = 0, a ∈ V3
|
| (EXT5)
| a ∧ b = - b ∧ a, a,b ∈ V3
|
証明
略■
空間内の二つのベクトル
aと
bが張る平行四辺形の面積量は
aから
bへ反時計回りに向かう角度を
θとすると次のように表すことができます。
これを座標表現で計算してみます。
| | | √λ12 + μ12 + ξ12√λ22 + μ22 + ξ22 |
|
|
|
| | |
| | 
| | (λ12 + μ12 + ξ12)(λ22 + μ22 + ξ22)
- (λ1λ2 + μ1μ2 + ξ1ξ2)2 |
| (λ12 + μ12 + ξ12)(λ22 + μ22 + ξ22) |
|
|
 | |
|
より、線長量の単位を
u = e1 = e2 = e3とすると
| | |
| | | √(λ12 + μ12 + ξ12)(λ22 + μ22 + ξ22)
- (λ1λ2 + μ1μ2 + ξ1ξ2)2 u ⊗ u |
|
| | | √( μ1 ξ2 - ξ1 μ2 )2
+ ( ξ1 λ2 - λ1 ξ2 )2
+ ( λ1 μ2 - μ1 λ2 )2
u ⊗ u |
|
となることから、三種類の有向面積量の直和
A23 ⊕ A31 ⊕ A12上のノルムを
| :
A23 ⊕ A31 ⊕ A12  A+ A+
|
| λ e2 ∧ e3 + μ e3 ∧ e1 +
ξ e1 ∧ e2 |
|
:= √λ2 + μ2 + ξ2 u ⊗ u
|
と定めると、
a ∧ bは二つのベクトル
a,bを含む平面上で
aと
bが張る平行四辺形の面積量に一致します。
空間内の二つのベクトル
a,bの外積
a ∧ bのノルム
a ∧ bは
aと
bが張る平行四辺形の面積量である。
二項外積は座標系に依存しますが、そのノルムは座標系に依存しない量です。
空間内の二つのベクトル
a,bのベクトル積
a × bは、これらのベクトルが張る向き付けられた平行四辺形に直交し、正方向にある。さらに、その単位線長比は平行四辺形の単位面積比に一致する。
証明
直交性は内積を計算するとわかる。
| | | λ1 ( μ1 ξ2 - ξ1 μ2 )
+ μ1 ( ξ1 λ2 - λ1 ξ2 )
+ ξ1 ( λ1 μ2 - μ1 λ2 ) |
|
| | | λ2 ( μ1 ξ2 - ξ1 μ2 )
+ μ2 ( ξ1 λ2 - λ1 ξ2 )
+ ξ2 ( λ1 μ2 - μ1 λ2 ) = 0 |
|
正方向であることは各射影平面における正方向成分であることからわかる。■
ベクトル積a × bは、向き付けられた平行四辺形の法線方向と面積とを同時に表現する空間的量になっています。
空間に付随するベクトル空間
V3上のベクトル積について次が成り立つ。
| (VEC1)
| ( a + b ) × c = a × c + b × c,
a,b,c ∈ V3
|
| (VEC2)
| a × ( b + c ) = a × b + a × c,
a,b,c ∈ V3
|
| (VEC3)
| λ a × b = λ a × b = a × λ b,
a,b ∈ V3, λ ∈ ℝ
|
| (VEC4)
| a × a = 0, a ∈ V3
|
| (VEC5)
| a × b = - b × a, a,b ∈ V3
|
証明
外積の性質による。■
ベクトル積は結合的ではありませんが、次の性質によりベクトル空間V3はLie環になります。
空間に付随するベクトル空間
V3上のベクトル積について次が成り立つ。
| (6.1) | | a × (b × c)
= 〈a,c〉b - 〈a,b〉c,
a,b,c ∈ V3
|
|
証明
略■
空間に付随するベクトル空間
V3上のベクトル積について次が成り立つ。
| (6.2) | | a × (b × c)
+ b × (c × a)
+ c × (a × b) = 0
, a,b,c ∈ V3
|
|
空間内の三つのベクトル
a,b,cの外積
a ∧ b ∧ cはそれらが張る平行六面体の有向体積量として定義されます。次の同値な三条件が満たされるときに正方向とし、そうでないときに負方向と定めます。
| (1)
| b ∧ cの正方向にaがある。
|
| (2)
| c ∧ aの正方向にbがある。
|
| (3)
| a ∧ bの正方向にcがある。
|
この定義により次の性質が成り立つことがわかります。
空間に付随するベクトル空間
V3上の三つのベクトルの外積
V3 × V3 × V3  D,
(a,b,c) D,
(a,b,c)  a ∧ b ∧ c a ∧ b ∧ c
|
は多重線形かつ交代であり、右手系の正規直交基底
(e1,e2,e3)を定めるとき、その単位を
uとすれば次が成り立つ。
証明
略■
三つのベクトル
a,b,cが次のように座標表現されているとします。
| a =
λ1 e1 + μ1 e2 + ξ1 e3
=
|  | |  |
|
| b =
λ2 e1 + μ2 e2 + ξ2 e3
=
| 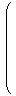 | | 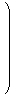 |
|
| c = λ3 e1 + μ3 e2 + ξ3 e3
=
| 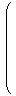 | | 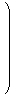 |
|
多重線形と交代性より
| a ∧ b ∧ c
=
det (a, b, c)
e1 ∧ e2 ∧ e3
|
となり、単位
uを使えば、
| a ∧ b ∧ c =
det (a, b, c) u ⊗ u ⊗ u
|
と書くことができます。これに測定写像
u-1:D =
ℝ u ⊗ u ⊗ u  ℝ,
a = ℝ,
a = | | u ⊗ u ⊗ u
 | |
|
を合成することにより、関数
detV3 × V3 × V3  ℝ,
(a,b,c) ℝ,
(a,b,c)  det (a,b,c) det (a,b,c)
|
が定まります。これは座標の取り方に依存するようですが、向きを変えない正規直交座標系の座標変換に関して不変です。
二項外積とベクトルとの外積を多重線形かつ交代となるように自然に拡張すると、例えば次のような計算ができます。
| | |
| |  λ3
λ3
| |
-
μ3
| |
+
ξ3
| |
 e1 ∧ e2 ∧ e3
e1 ∧ e2 ∧ e3
|
|
| | |
関数
detは
(3,3)行列に対する行列式を定めます。
行列式は乗法群としての準同型写像になっています。
証明
略■
体積量表現a ∧ b ∧ cと体積比表現det ( a, b, c )は区別して使うことにします。
数 学
ベクトル積 べくとるせき, vector product
法線ベクトル ほうせんべくとる, normal vector