6.2節 ノルムと内積
著者:梅谷 武
語句:ノルム, 内積
空間に付随するベクトル空間上のノルムと内積を定義する。
作成:2009-09-16
更新:2011-03-08
空間に付随するベクトル空間
V3に属するベクトル
aは空間内の二点
P,Qによって、
a = [PQ]と表されます。このとき、ベクトルの長さによってノルムを定義します。
空間に付随するベクトル空間
V3上のノルムは次の性質を満たす。
| (N1)
| a ≧ 0, a ∈ V3かつa = 0 ⇔ a = 0 |
| (N2)
| λ a = λ a,
a ∈ V3, λ ∈ ℝ |
| (N3)
| a + b ≦ a + b,
a,b ∈ V3 |
証明
略■
正規直交座標系
(O;e1,e2,e3)を定め、任意のベクトル
aを
と座標表現します。線長量
u = e1 = e2 =
e3を単位として線分の長さを測るとき、
a = λ uとおくと、ピュタゴラスの定理から
| λ u ⊗ λ u =
| | u ⊗ | | u +
| | u ⊗ | | u +
| | u ⊗ | | u
|
が成り立ち、テンソル積の双線形性により、
となり、
と求めることができます。
ノルムに単位
uによる測定写像
u-1:L = ℝu  ℝ,
a = ℝ,
a = | | u  u-1(a) = u-1(a) = | |
|
を合成すると
V3  ℝ+,
a ℝ+,
a  u-1( u-1( | | ) =
λ = √μ2 + ν2 + ξ2
|
となります。以後、座標表現されている場合は原則として測定写像を合成します。
空間内の二点
P,Qの距離は
d(P,Q) = [PQ]によって定義されていましたから
が成り立ちます。
空間内の二つのベクトル
a,bの内積は、それらが同一平面上にあることから平面ベクトルの内積と同様に定義することができます。
V3 × V3  A,
(a,b) A,
(a,b)  〈a,b〉 :=
cos θ 〈a,b〉 :=
cos θ | | ⊗ | |
|
正規直交座標系
(O;e1,e2,e3)を定めたときの内積の座標表現を求めます。二つのベクトル
a,bが次のように座標表現されているとします。
| | | λ1 e1 + μ1 e2 + ξ1 e3
=
|  | |  |
|
|
| | | λ2 e1 + μ2 e2 + ξ2 e3
=
|  | |  |
|
このとき余弦定理から次の公式が導かれます。
| (6.2) | | cos θ = | | √λ12 + μ12 + ξ12√λ22 + μ22 + ξ22 |
|
|
|
|
線長量の単位
uによって
| | | √λ12 + μ12 + ξ12 u ⊗ √λ22 + μ22 + ξ22 u |
|
| | | √λ12 + μ12 + ξ12
√λ22 + μ22 + ξ22 u ⊗ u |
|
と書くことができますから、測定写像
u-1:A = ℝ u ⊗ u  ℝ,
a = ℝ,
a = | | u ⊗ u  | |
|
を合成すると次のようになります。
V3 × V3  ℝ,
(a,b) ℝ,
(a,b)  u-1(〈a,b〉) = λ1 λ2 + μ1 μ2 + ξ1ξ2 u-1(〈a,b〉) = λ1 λ2 + μ1 μ2 + ξ1ξ2
|
以後、座標表現されている場合には原則として測定写像を合成します。
| 〈a,b〉
=
ta b
=
( λ1 μ1 ξ1 )
|  | |  |
=
λ1 λ2 + μ1 μ2 + ξ1ξ2
|
空間に付随するベクトル空間
V3上の内積は双線形かつ対称、正値である。すなわち、次が成り立つ。
| (IN1)
| 〈 a + b, c 〉 = 〈 a, c 〉 + 〈 b, c 〉,
a,b,c ∈ V3
|
| (IN2)
| 〈 a, b + c 〉 = 〈 a, b 〉 + 〈 a, c 〉,
a,b,c ∈ V3
|
| (IN3)
| λ 〈 a, b 〉 = 〈 λ a, b 〉 = 〈 a, λ b 〉,
a,b ∈ V3, λ ∈ ℝ
|
| (IN4)
| 〈 a, b 〉 = 〈 b, a 〉,
a,b ∈ V3
|
| (IN5)
| 〈 a, a 〉 ≧ 0, a ∈ V3
かつ
〈 a, a 〉 = 0 ⇔ a = 0
|
証明
略■
証明
略■
空間内の任意のベクトル
a,bについて、次が成り立つ。
| (6.4) | | 〈 a, b 〉 = | |
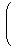
| | ⊗ | | -
| | ⊗ | | -
| | ⊗ | |
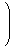
|
|
証明
略■
空間内の任意のベクトル
a,bについて、次が成り立つ。
証明
略■
空間に付随するベクトル空間
V3上の正規直交基底
(e1,e2,e3)について、次が成り立つ。
| (6.6) | | 〈 ei, ej 〉 = δij, i,j = 1,2,3
|
|
証明
略■