6.1節 空間ベクトル
著者:梅谷 武
語句:空間ベクトル, 空間座標系
空間ベクトルを定義し、空間に付随するベクトル空間が三次元実線形空間であることを示す。
作成:2009-09-16
更新:2011-03-08
空間U内に二点A,Bが与えられたときに、公準1によってそれらを線分で結ぶことができます。空間内の有向線分とは二点間を結ぶ線分において始点と終点を指定したものです。
有向線分は空間上の平行移動を定め、二つの有向線分が同じ平行移動を定めるという関係は同値関係になります。
Arrow3 = { 空間U内の有向線分全体 }として、
Arrow3をこの同値関係
∼で分割したものを
V3× := Arrow3/∼と書き、その元をベクトルと呼びます。平面上の平面ベクトルと区別したいときには
空間ベクトルくうかんべくとる, space vectorと呼びます。
V3×の二つのベクトルの加法を、それらが置かれた平面上の加法として定義します。始点と終点が一致するものも有向線分と考え、これにより生成されるベクトルを0とします。V3 := V3× ∪ {0}を空間Uに付随するベクトル空間と呼びます。a ∈ V3について、有向線分AB ∈ aを適当に選び、これの始点と終点を入れ替えたものを含むベクトルを-a = [BA]と定めるとV3は加法群になります。0は零元で、任意の元aについて-aが逆元です。
空間
Uにベクトル空間
V3が付随していると考えるとき、
(U,V3)と書きます。
P ∈ U, a ∈ V3が与えられたとき、始点を
Pとする有向線分
PQ ∈ aを選び、
U × V3  U, (P,a) U, (P,a)  Q := P + a Q := P + a
|
と定めることによってベクトル空間
V3は加法群として空間
Uに右から作用します。
V3の加法は
| (P + a) + b = P + (a + b),
P ∈ U, a, b ∈ V3
|
が成り立つように定義されています。加法群は可換ですからこれは左からの作用と考えることもできますが、慣例により、右からの作用として表記します。
空間
(U,V3)において、原点
Oと
Oを通る平面と、その平面上の正規直交基底
(e1,e2)を定めます。命題XI-12「平面上に与えられた点から垂線を立てること。」により、
Oからその平面に垂線を立て、その垂線上に原点
Oを始点とし、長さが与えられた基底ベクトルと同じ有向線分を定め、それが属するベクトルを
e3とします。命題XI-13「異なる二直線を平面上の同じ点から同じ方向へ垂直に立てることはできない。」により、このような平面上の正規直交基底の拡張は一回しかできません。これにより空間内の任意の点
Pは
| P = O + λ1 e1 + λ2 e2 + λ3 e3,
λ1,λ2,λ3 ∈ ℝ
|
と一意的に表現することができます。
空間
Uに付随するベクトル空間
V3の元は、空間
U内の有向線分の同値類ですから、任意の元
a ∈ V3はある点
P ∈ Uによって、
と書くことができ、次の命題が成り立ちます。
空間
(U,V3)に付随するベクトル空間
V3は三次元実線形空間であり、正規直交基底となるベクトルの組
(e1,e2,e3)により、
と表すことができる。
空間
(U,V3)に付随するベクトル空間
V3の任意の元
aは正規直交基底
(e1,e2,e3)により一意的に
| a = λ1 e1 + λ2 e2 + λ3 e3,
λ1, λ2,λ3 ∈ ℝ
|
と表され、写像
V3  ℝ3,
a ℝ3,
a  (λ1, λ2, λ3) (λ1, λ2, λ3)
|
は実線形空間としての同型を与えます。このとき、さらに
Uの原点
Oを与えることにより、空間座標系
(O;e1,e2,e3)が定まります。
空間
U上の任意の点
Pに対して
なる
aが一意的に定まりますから、正規直交基底
(e1,e2,e3)を使って
| P = O + λ1 e1 + λ2 e2 + λ3 e3,
λ1, λ2,λ3 ∈ ℝ
|
と表現することができます。この対応により定まる写像
U  ℝ3,
P ℝ3,
P  (λ1, λ2, λ3) (λ1, λ2, λ3)
|
は全単射であり、
(λ1, λ2, λ3)を点
Pの座標と呼びます。
点
P,Qの座標を
(λ1, λ2, λ3), (μ1, μ2, μ3)とするとき、有向線分
PQの定めるベクトルを求めてみましょう。
| | | O + λ1 e1 + λ2 e2 + λ3 e3 |
|
| | | O + μ1 e1 + μ2 e2 + μ3 e3 |
|
より、
であり、
PQ = OQ - OPから、
| [PQ] =
(μ1 - λ1) e1 + (μ2 - λ2) e2
+ (μ3 - λ3) e3
|
となります。
空間内の平面上に平面座標系(O;e1,e2)を定め、それに垂直な基底ベクトルe3を決めるときに、その決め方は二通りあります。それは平面によって空間が二つの領域に分割されるからです。そのどちらに原点を始点とする有向線分が属するかということを二つのベクトルの外積を利用して表現します。
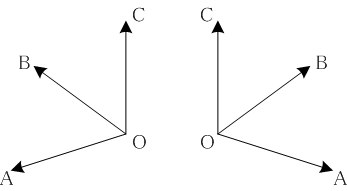
外積e1 ∧ e2が定める平行四辺形が表になる方向を正の方向、裏になる方向を負の方向と定めます。そして、e3が外積e1 ∧ e2の正の方向にあるとき、空間座標系(O;e1,e2,e3)は右手系であるといい、負の方向にあるとき、左手系であるといいます。
OA ∈ e1,
OB ∈ e2,
OC ∈ e3
として左手系を左に、右手系を右に図示します。
空間(U,V3)において、二つの座標系(O;e1,e2,e3),(O';e1',e2',e3')が与えられたとしましょう。このとき、二つの座標系で表現される二つの座標の間の関係について考えます。
まず、後の座標系を前の座標系で表しておきます。
| | |
| | |
| | |
| | | O + t1 e1 + t2 e2 + t3 e3 |
|
任意の点
Pを与え、その
(O;e1,e2,e3)による座標を
(p1, p2, p3)、
(O';e1',e2',e3')による座標を
(p1', p2', p3')とします。
| | | O + p1 e1 + p2 e2 + p3 e3 |
|
| | | O' + p1' e1' + p2' e2' + p3' e3' |
|
それぞれ代入すると
| | | O + t1 e1 + t2 e2 + t3 e3
+ p1' e1' + p2' e2' |
|
| | | O + t1 e1 + t2 e2 + t3 e3 |
|
| | | + p1' a11 e1 + p1' a21 e2 + p1' a31 e3 |
|
| | | + p2' a12 e1 + p2' a22 e2 + p2' a32 e3 |
|
| | | + p3' a13 e1 + p3' a23 e2 + p3' a33 e3 |
|
| | |
| | | + ( t1 + p1' a11 + p2' a12 + p3' a13 ) e1 |
|
| | | + ( t2 + p1' a21 + p2' a22 + p3' a23 ) e2 |
|
| | | + ( t3 + p1' a31 + p2' a32 + p3' a33 ) e3 |
|
係数を比較すると
| | | t1 + p1' a11 + p2' a12 + p3' a13 |
|
| | | t2 + p1' a21 + p2' a22 + p3' a23 |
|
| | | t3 + p1' a31 + p2' a32 + p3' a33 |
|
これを行列表現します。
さらにまとめて行列表現します。
同じように座標系
(O';e1',e2',e3')から
(O'';e1'',e2'',e3'')への座標変換
が与えられたとしましょう。このとき、座標変換を合成して座標系
(O;e1,e2,e3)から
(O'';e1'',e2'',e3'')への座標変換を作ることができます。
二つの変換行列の積が合成した座標変換の変換行列になります。
もし、(O;e1,e2,e3)と(O'';e1'',e2'',e3'')が
一致していれば、合成した変換行列は単位行列になりますから、逆変換の行列は元の行列の逆行列になることがわかります。
数 学
空間ベクトル くうかんべくとる, space vector