2.5節 外積
著者:梅谷 武
語句:外積, 行列式
平面に付随するベクトル空間の外積について述べる。
作成:2009-09-01
更新:2011-03-08
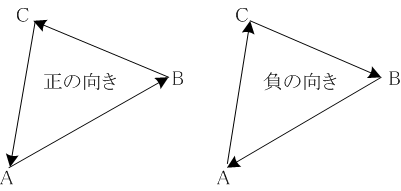
直線は平面を二つの領域に分割します。有向線分が与えられた場合、分割された領域の右側と左側が識別することができるようになります。直線図形をその境界の頂点列ABCで表すときに直線図形の内部が有向線分AB, BC, CAの左側にあるとき、または回転が反時計回りであるとき、直線図形ABCは正の向きであるといい、右側にあるとき、回転が時計回りであるとき、負の向きであるといいます。正の向きの場合は表面、負の向きの場合は裏面を見ていると考えます。
向き付けられた平面図形の面積は正の向きの場合は正の面積量、負の向きの場合は負の面積量であると定めると、面積量は向き付けられた平面図形の面積を表していると考えることができます。
内積の定義において、余弦を正弦に変えると二つのベクトルa,bが張る平行四辺形の面積になることに気が付きます。そこで次のような新しい計量を定義してみましょう。
二つのベクトルが同じ場合は
と定義するのが妥当です。このことから
| (a+b) ∧ (a+b) = a ∧ b + b ∧ a = 0
|
となり、
が導かれます。この性質に合うように正弦の定義を次のように拡張します。
| 無角・平角のとき
| |
| 直角のとき
| |
| 三直角のとき
| |
| 上記以外で平角より小さいとき
| |
| 上記以外で平角より大きいとき
| |
その上で、
a ∧ bの定義における角
θを
aから
bへ反時計回りに向かう角と定めます。
平面に付随するベクトル空間
V2上の外積は双線形かつ交代である。すなわち、次が成り立つ。
| (EXT1)
| ( a + b ) ∧ c = a ∧ c + b ∧ c,
a,b,c ∈ V2
|
| (EXT2)
| a ∧ ( b + c ) = a ∧ b + a ∧ c,
a,b,c ∈ V2
|
| (EXT3)
| λ a ∧ b = λ a ∧ b = a ∧ λ b,
a,b ∈ V2, λ ∈ ℝ
|
| (EXT4)
| a ∧ a = 0, a ∈ V2
|
| (EXT5)
| a ∧ b = - b ∧ a, a,b ∈ V2
|
証明
略■
二つのベクトル
a,bが次のように座標表現されているとします。
| | | λ1 e1 + μ1 e2 =
| 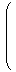 | | 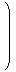 |
|
| | | λ2 e1 + μ2 e2 =
| 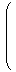 | | 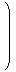 |
|
このとき、
| | | ( λ1 e1 + μ1 e2 ) ∧ ( λ2 e1 + μ2 e2 ) |
|
| | | λ1 e1 ∧ ( λ2 e1 + μ2 e2 )
+ μ1 e2 ∧ ( λ2 e1 + μ2 e2 ) |
|
| | | λ1 μ2 e1 ∧ e2
+ μ1 λ2 e2 ∧ e1 |
|
| | |
より、写像
V2 × V2  ℝ,
(a,b) ℝ,
(a,b)  det(a,b) := λ1 μ2 - μ1 λ2 det(a,b) := λ1 μ2 - μ1 λ2
|
が定まります。これは座標系の取り方に依存するようですが、向きを変えない正規直交座標系の座標変換に関して、この値が不変であることが後にわかります。
平面に付随するベクトル空間
V2において正規直交座標系を定めることによって定義される写像
det : V2 × V2  ℝ,
(a,b) ℝ,
(a,b)  det(a,b) det(a,b)
|
は交代双線形形式である。
証明
略■
行列式は乗法群としての準同型写像になっています。
証明
略■
外積を座標表現すると
となり、線長量の単位
u = e1 = e2を使えば、
と書くことができます。これに測定写像
u-1 : A =
ℝ u ⊗ u  ℝ,
a= ℝ,
a= | | u ⊗ u  | |
|
を合成すると行列式に一致します。
V2 × V2  ℝ,
(a, b) ℝ,
(a, b)  u-1(a ∧ b) =
det(a, b) u-1(a ∧ b) =
det(a, b)
|
外積については、面積量表現を
a ∧ b、面積比表現を
det( a, b )として区別することにします。
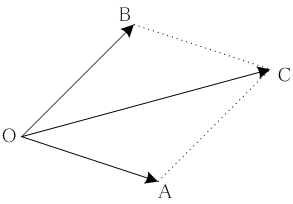
平面の原点Oを始点とするa,bに属する有向線分をOA, OBとし、それらの和をOCとすると、外積a ∧ bは有向平行四辺形OACBの面積量に一致します。
数 学
外積 がいせき, exterior product
行列式 ぎょうれつしき, determinant