2.4節 ノルムと内積
著者:梅谷 武
語句:ノルム, 内積, クロネッカーのデルタ
平面に付随するベクトル空間のノルムと内積について述べる。
作成:2009-09-01
更新:2011-03-08
2.4 ノルムと内積
2.4.1 ベクトル空間のノルム
 平面に付随するベクトル空間V2のノルムはベクトルの長さとして自然に定義することができます。ベクトルa ∈ V2は平面上に二点P,Qをとって、a=[PQ]と表わすことができます。このとき、
a
 := [PQ]
によって、ノルム
  
:V2 longrightarrow L+,  a longmapsto
a
を定めます。

命題2.4.1.2 ノルムの性質

平面に付随するベクトル空間V2は次のノルムとしての性質を満たす。
(N1) a ≧ 0かつa = 0 ⇔ a = 0,  a ∈ V2
(N2) λ a = λ a,  λ ∈ ℝ,  a ∈ V2
(N3) a + b ≦ a + b,  a,b ∈ V2

証明

(N3) 命題I-20「任意の三角形において、任意の二辺の和は、残りの辺より大きい。」■
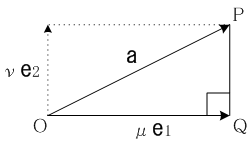
 平面上に正規直交座標系(O;e1,e2)を定めるとき任意のベクトルaは、
a = μ e1 + ν e2
と座標表現することができます。さらに平面上の点P,Qによってa=[OP],  μ e1=[OQ], ν e2=[QP]と表すことができ、三角形OPQは角OQPを直角とする直角三角形になります。
図2.4.1.5 正規直交座標系のノルム
正規直交座標系のノルム
 命題I-47「直角三角形において、直角に対する辺上の正方形は、直角を挟む辺上の正方形の和に等しい。」を面積量Aの等式として表現すれば、
a
 ⊗
a
 =
μ e1
 ⊗
μ e1
 +
ν e2
 ⊗
ν e2
となり、線長量u = e1 = e2を単位とすれば、a = λ uとおくと
λ u ⊗ λ u = |μ| u ⊗ |μ| u + |ν| u ⊗ |ν| u
が成り立つことから、
λ2 = μ2 + ν2
となり、
λ = √μ2 + ν2
が得られます。
 正規直交座標系においては線長量Lの単位u ∈ L+が決められていますから、 ノルムに単位uによる測定写像
u-1:L = ℝ u longrightarrow ℝ,  a =
a
u
u longmapsto u-1(a) =
a
u
を合成すると、ノルムは
  
:V2 longrightarrow ℝ+,  a longmapsto u-1(
a
) = λ = √μ2 + ν2
という非負の実数値関数となり、この関数もノルムの性質を満たします。
 平面上の二点P,Qの距離はd(P,Q) = [PQ]によって定義されていましたから、距離はノルムによって表わすことができます。

命題2.4.1.9 平面上の距離のノルムによる表現

平面上の二点P,Qの距離について、次が成り立つ。
(2.1)
d(P,Q) =
[PQ]
 =
[OP] - [OQ]
2.4.2 ベクトル空間の内積
 平面幾何においてはさまざまな状況で二つのベクトルの関係性について考えることが求められますが、内積はそのための計量技法の一つです。
 平面上に二つのベクトルa,bが与えられたとき、原点Oを定めると、二点P,Qによりa = [OP], b = [OQ]と表すことができます。このとき、原論はθ = ∠POQが直角であるか(命題I-47)、鈍角であるか(命題II-12)、鋭角であるか(命題II-13)の三つの場合に分け、次のようにピュタゴラスの定理における面積補正を行っています。
直角のとき
補正無し
鈍角のとき
cos θ
a
 ⊗
b
を加える
鋭角のとき
cos θ
a
 ⊗
b
を引く
この補正量が内積に他なりません。ここで、1.10節における余弦の定義を次のように拡張しておきます。
無角のとき
cos θ = 1
鋭角のとき
cos θ =
d
b
直角のとき
cos θ = 0
鈍角のとき
cos θ = -
d
b
平角のとき
cos θ = -1
これによりピュタゴラスの定理の拡張を次のように表現できます。

定理2.4.2.3 余弦定理

平面上の二つのベクトルa,bを、原点Oを始点とする有向線分により、a = [OP],  b = [OQ] と表わすとき、c = [PQ], θ=∠POQとおくと次が成り立つ。
(2.2)
c
 ⊗
c
 =
a
 ⊗
a
 +
b
 ⊗
b
 - 2 cos θ
a
 ⊗
b
 正規直交基底
e1 = lb72
1
0
rb72,   e2 = lb72
0
1
rb72
によって、二つのベクトルa,bが次のように座標表現されているとします。
                         a
=
λ1 e1 + μ1 e2   = lb72
λ1
μ1
rb72
b
=
λ2 e1 + μ2 e2   = lb72
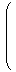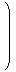λ2
μ2
rb72
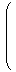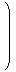このとき余弦定理は次のように表現されます。
                    
(λ2 - λ1)2 + (μ2 - μ1)2
=
(λ12 + μ12) + (λ22 + μ22) - 2 cos θ √λ12 + μ12 √λ22 + μ22
 cos θに関して整理すると次の公式が導かれます。

命題2.4.2.6

(2.3)
cos θ =
λ1λ2 + μ1μ2
√λ12 + μ12 √λ22 + μ22

定義2.4.2.7 内積

平面に付随するベクトル空間V2上の内積ないせき, inner productを次のように定義する。
V2 × V2 longrightarrow A,  (a, b) longmapsto 〈 a, b 〉 := cos θ
a
 ⊗
b
 正規直交座標系(O;e1,e2)が与えられているときは、線長量の単位uによって
          
a
 ⊗
b
=
√λ12 + μ12 u ⊗ √λ22 + μ22 u
=
√λ12 + μ12√λ22 + μ22(u ⊗ u)
と書くことができます。測定写像
u-1:A = ℝ u ⊗ u longrightarrow ℝ,  a=
a
u ⊗ u
u ⊗ u longmapsto
a
u ⊗ u
を合成すると次のようになります。
V2 × V2 longrightarrow ℝ,  (a, b) longmapsto u-1(〈a, b〉) = λ1 λ2 + μ1 μ2
以後、簡単のために測定写像を合成した場合でもu-1(〈⋯, ⋯〉)を単に〈⋯, ⋯〉と書くことにします。
〈a, b〉 = ta b = ( λ1 μ1 ) lb72
λ2
μ2
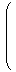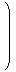rb72 = λ1 λ2 + μ1 μ2

命題2.4.2.9 内積の性質

平面に付随するベクトル空間V2上の内積は双線形かつ対称、正値である。すなわち、次が成り立つ。
(IN1) 〈 a + b, c 〉 = 〈 a, c 〉 + 〈 b, c 〉,  a,b,c ∈ V2
(IN2) 〈 a, b + c 〉 = 〈 a, b 〉 + 〈 a, c 〉,  a,b,c ∈ V2
(IN3) λ 〈 a, b 〉 = 〈 λ a, b 〉 = 〈 a, λ b 〉,  a,b ∈ V2, λ ∈ ℝ
(IN4) 〈 a, b 〉 = 〈 b, a 〉,  a,b ∈ V2
(IN5) 〈 a, a 〉 ≧ 0, a ∈ V2 かつ 〈 a, a 〉 = 0  ⇔  a = 0

証明

略■

命題2.4.2.11 内積とノルム(I)

平面上の任意のベクトルaについて、次が成り立つ。
(2.4)
a
 = √〈 a, a 〉

証明

〈a, a〉 =
a
 ⊗
a
は一辺の長さがaであるような正方形の面積量であるから、これを正方化すればその一辺の長さaになる。■

命題2.4.2.13 内積とノルム(II)

平面上の任意のベクトルa,bについて、次が成り立つ。
(2.5)
〈 a, b 〉 =
1
2
 lb36
a + b
 ⊗
a + b
 -
a
 ⊗
a
 -
b
 ⊗
b
 rb36

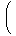証明

          〈 a + b, a + b 〉
=
〈 a, a 〉 + 〈 a, b 〉 + 〈 b, a 〉 + 〈 b, b 〉
=
a
 ⊗
a
 +
b
 ⊗
b
 + 2 〈 a, b 〉
■

命題2.4.2.15 シュヴァルツの不等式

平面上の任意のベクトルa,bについて、次が成り立つ。
(2.6)
〈 a, b 〉
 ≦
a
 ⊗
b

証明

〈 a, b 〉
 =
cos θ
a
 ⊗
b
 ≦
a
 ⊗
b
■

定義2.4.2.17 クロネッカーのデルタ

写像
ℕ × ℕ longrightarrow {0,1},  (i, j) longmapsto δij
δij = lc72
0,
i
≠
j
1,
i
=
j
をクロネッカーのデルタくろねっかーのでるた, Kronecker deltaと呼ぶ。

命題2.4.2.18 正規直交性

平面に付随するベクトル空間V2上の正規直交座標系(O;e1,e2)について、次が成り立つ。
(2.7)
〈 ei, ej 〉 = δij,  i,j = 1,2

証明

略■
数　　学
内積 ないせき, inner product
クロネッカーのデルタ くろねっかーのでるた, Kronecker delta
 
Published by SANENSYA Co.,Ltd.