第1章において、原論を幾何学の基礎とするために自然哲学的な議論を積み重ねてきました。この第2章以降では、幾何学の理論を実際に現場で使えるような形式で表現するとともに、その際にどうしても必要となる解析学の技法を使います。

 これまで原論の立場を尊重して、完備性を仮定しないで議論を進めてきましたが、今後は平面や線長量、線長比の完備性を仮定し、実数論に基づく解析学の結果を利用することがあります。そのため線長比R_Lを実数ℝと同一視し、線長量のような線長比R_L上の線形空間を、実数ℝ上の線形空間として実線形空間じつせんけいくうかん, real linear spaceと略します。

 しかし、数とは自然数や整数のことであり、有理数は数比であり、実数は量比であるという立場には変わりがありません。説明や証明においてもなるべく第1章で準備した概念に基づくことにします。

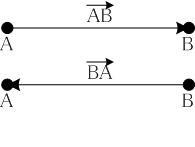
 平面を点集合Eで表すことにします。平面E上に二点A,Bが与えられたときに、公準1によってそれらを線分で結ぶことができます。有向線分ゆうこうせんぶん, oriented segmentとは二点間を結ぶ線分において始点と終点を指定したものです。始点Aと終点Bを結ぶ有向線分をABと書くことにします。始点と終点の順序は線分の向きを定めており、同じ二点でも始点と終点を入れ替えたものは異なる有向線分を表しています。したがって、A ≠ B ⇒ AB ≠ BAが成り立ちます。

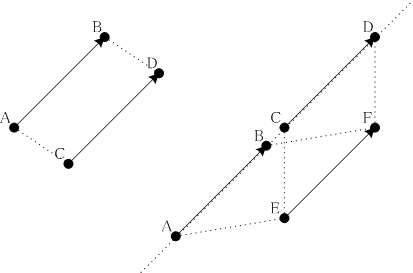
 有向線分は平面上の平行移動を定めます。実際、有向線分をABが与えられたとき、任意の点Cについて、Cが直線AB上になければ、点DをABとCDが平行でかつACとBDが平行になるようにとることができます。Cが直線AB上にあるときは直線AB上にない点Eをとり、点FをABとEFが平行でかつAEとBFが平行になるようにします。さらに点DをEFとCDが平行でかつECとFDが平行になるようにとることができます。このようにして、平面E上の任意の点を有向線分ABの方向に同じ長さだけ平行移動することができます。

 二つの有向線分が同じ平行移動を定めるという関係は同値関係になります。Arrow² = { 平面E上の有向線分全体 }として、この同値関係∼で分割したものをV^2× := Arrow²/∼と書き、その元をベクトルべくとる, vectorと呼びます。

 有向線分が始点から終点までの線分という図形であるのに対し、ベクトルは平面上のすべての点に一斉に作用する機能をもっています。

 ABの同値類としてのベクトルは[AB]と表されます。またV^2×の元としてのベクトルを太字の英小文字でaのように記すことにします。aがABを含む場合は、 あるいは と表されます。

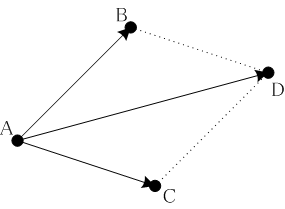
 V^2×に加法を定義します。a, b ∈ V^2×について、有向線分AB ∈ aを適当に選び、Aを始点とするAC ∈ bを選びます。そして、ABをCを始点とするように平行移動させたときの終点をDとします。このとき、有向線分ADが生成するベクトルをa + b := [AD]と定めます。

 始点と終点が一致するものも有向線分と考え、これにより生成されるベクトルを0とします。を平面Eに付随するベクトル空間べくとるくうかん, vector spaceと呼びます。a ∈ V²について、有向線分AB ∈ aを適当に選び、これの始点と終点を入れ替えたものを含むベクトルを-a = [BA]と定めるとV²は加法群になります。0は零元で、任意の元aについて-aが逆元です。

 平面Eにベクトル空間V²が付随していると考えるとき、(E,V²)と書きます。P ∈ E, a ∈ V²が与えられたとき、始点をPとする有向線分PQ ∈ aを選び、 と定めることによってベクトル空間V²は加法群として平面Eに右から 作用します。V²の加法は が成り立つように定義されています。加法群は可換ですからこれは左からの作用と考えることもできますが、慣例により、右からの作用として表記します。

 任意のP,Q ∈ Eについて、a = [PQ] ∈ V²によりP + a = Qとすることができます。この性質は群が推移的すいいてき, transitiveに作用しているといわれ、このとき、群が作用する集合は等質空間とうしつくうかん, homogeneous spaceと呼ばれます。平面(E,V²)において、平面Eは変換群V²の等質空間です。また、P + a = Pであればa = 0となります。これを群が忠実ちゅうじつ, faithfulに作用しているといいます。

 平面E上の点Oとその点を通る無限直線αが与えられたとき、 と定めると加法群としてV²の部分群になり、直線αに右から推移的に作用します。直線αにベクトル空間V_αが付随していると考えるとき、(α,V_α)と書きます。

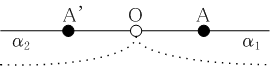
 Oと異なる点Aを固定します。このとき、直線αから点Oを除くと、二つの連結領域α₁,α₂に分割されます。Aはそのどちらかに含まれますが、A ∈ α₁であるとします。

 このとき、 とおくと、V_α = V_α1 ∪ {0} ∪ V_α2と分割されます。V_α1, V_α2はそれぞれ同一直線上の同じ方向をもつベクトルを集めた集合ですが、その集合内では方向無しで長さだけで元を識別できることから線分の等長類である線長量とみなすことができます。V_α1を線長量の正の部分L⁺に対応させ、V_α2を負の部分L^-に対応させ、0ベクトルに零元を対応させることによりV_α ≅ L、すなわち一次元実線形空間として同じものと考えることができます。

 e := [OA]はV_αの基底になります。

 直線α上の0でないベクトル全体の集合 の比 について考えます。これは第１章で考えた無向量の比ではなく、ベクトルという有向量の比ですが、方向を反転する負をとる操作が加法の中に自然に組み込まれているために比例の定義をそのまま拡張することができます。

 これにより、直線上のベクトル比全体の集合ℛ_Vα^×を比例関係∝で分割した同値類の集合R_Vα^× := ℛ_Vα^×/∝を考えることができますが、これは対称化した線長比ℝ^×に一致します。

 V_αの実線形空間としての自己同型群について考えます。線形空間の自己同型写像は正則せいそく, regularな線形変換と呼ばれます。V_α上の正則な実線形変換のなす群は一般線形群いっぱんせんけいぐん, general linear groupと呼ばれ、GL(V_α, ℝ)という記号で表されます。

 線長論により、二つの線長比が比例するとはそれらが定める線長量上の比を保存する変換、すなわち相似変換が等しいことであることが導かれました。これは対称化しても成り立ち、直線上のベクトル比が比例するとはそれらが定める直線上の相似変換が等しいことと同等です。一次元実線形空間においては、相似変換と正則な線形変換は一致しますから、一般線形群GL(V_α, ℝ)は、直線上のベクトル比、言い換えれば対称化した線長比ℝ^×に一致することがわかります。

 線長比ℝ^×は直線上のベクトル比を比例類として表現したものであり、一般線形群GL(V_α, ℝ)は相似変換として表現したものに他なりません。