1.8節 線長量の線形代数
著者:梅谷 武
語句:線形空間, 線形写像, 線形形式, 線形独立, 基底, 次元, 座標, 単位, 測定, 双対空間, 双対性
線長量が一次元線形空間であること、単位と測定が双対関係にあることを示す。
作成:2009-08-27
更新:2011-03-08
1.8 線長量の線形代数
1.8.1 線形空間と基底
 環Rと加群Mにおいて作用
R × M longrightarrow M,  (a,x) longmapsto ax
が定められていて、
(1) a(x + y) = ax + ay,  a ∈ R, x,y ∈ M
(2) (a + b)x = ax + bx,  a,b ∈ R, x ∈ M
(3) (ab)x = a(bx),  a,b ∈ R, x ∈ M
(4) 1x = x,  1 ∈ R, x ∈ M
が成り立つときにRをMの作用域さよういき, operator domain、Mを作用域Rをもつ加群、R上の加群、あるいはR-加群といいます。
 ここまでの議論によって、線長量Lはアルキメデス的順序体RL上の加群であることがわかりました。R-加群においては慣例としてRの元は係数と呼ばれ、axは係数倍と呼ばれますが、原論の立場ではRLは数ではなく、あくまでも比ですから、それぞれ比、比例倍というような言い方が適切でしょう。
 体上の加群は線形空間と呼ばれますが、これを改めて定義します。

定義1.8.1.4 線形空間

体Kと加群Vについて、作用
K × V longrightarrow V,  (λ,a) longmapsto λ a
が定義され、次の条件が満たされるとき、VをK上の線形空間せんけいくうかん, linear spaceという。
(LS1) 1 a = a,  1 ∈ K, a ∈ V
(LS2) (λ μ)a = λ (μ a),  λ, μ ∈ K, a ∈ V
(LS3) (λ + μ)a = λ a + μ a,  λ, μ ∈ K, a ∈ V
(LS4) λ (a + b) = λ a + λ b,  λ ∈ K, a, b ∈ V

定義1.8.1.5 線形写像

V,WをK上の線形空間とするとき、加群としての準同型写像f:V → Wが
f(λ a) = λ f(a),  λ ∈ K, a ∈ V
を満たすとき、K-線形写像せんけいしゃぞう, linear mappingという。特にK自身をK上の線形空間とみたとき、K-線形写像をK-線形形式せんけいけいしき, linear formという。また、Vから自分自身への線形写像を線形変換せんけいへんかん, linear transformationという。
 体K上の線形空間において、その元の列{ e1, ⋯, ek }, k ∈ ℕの線形結合せんけいけつごう, linear combinationとは次の形で表現されるものです。
λ1 e1 + ⋯ + λk ek,  λ1, ⋯, λk ∈ K
この元の列が線形独立せんけいどくりつ, linearly independentであるとは、
λ1 e1 + ⋯ + λk ek = 0  ⇒  λ1 = ⋯ = λk = 0
が成り立つことです。線形独立でないとき線形従属せんけいじゅうぞく, linearly dependentであるといいます。

命題1.8.1.7

線形独立な元の列{ e1, ⋯, ek }, k ∈ ℕの線形結合は一意的な表現である。すなわち、
λ1 e1 + ⋯ + λk ek = μ1 e1 + ⋯ + μk ek  ⇒ λi = μi,  i = 1, ⋯, k

証明

略■
 体K上の線形空間Vの基底きてい, basisとは線形独立な元の列であって、Vを生成するもののことです。すなわち、Vの任意の元がその元の列の線形結合として表現されることです。
 体Kのn個の直積
Kn := { (λ1, λ2, ⋯ ,λn) | λi ∈ K,  i = 1, ⋯, n }
に対して、K上の作用を
μ (λ1, λ2, ⋯ ,λn) := (μ λ1, μ λ2, ⋯ ,μ λn)
と定めることによって体K上の線形空間になります。

命題1.8.1.11

体K上の線形空間Vがn個の基底を持てば、Knに同型である。

証明

略■
 異なる自然数m,nに対してKmとKnは同型にはなりませんから、上の命題は有限個の基底をもつ線形空間の代数的構造は、基底を成す元の個数によって決定されることを意味しています。
 体K上の線形空間Vが有限個の基底をもつとき、その個数を線形空間の次元じげん, dimensionと呼び、
dimK V
と書くことにします。
1.8.2 単位と測定
 線分の長さを測るとは、単位u ∈ L+を定めて、測定対象となる線分a ∈ L+との比a:uを求めることです。これは自己同型写像として考えると
a =
a
u
u,  a ∈ L+
なる比を求めることです。これがどんな線分についても可能であることを、
L+ = RL+ u := { λ u | λ ∈ RL+ }
というように表現します。このことをL+はRL+上単位uによって生成せいせい, generateされるといいます。これは線長量を対称化してもそのまま成り立ち、LはRL上単位uによって生成されます。
L = RL u := { λ u | λ ∈ RL }
 ここまでの結果をまとめます。

命題1.8.2.3

線長量Lは線長比RL上の一次元線形空間であり、正の元u ∈ L+を単位とすると、uは基底となり、LはRL上uによって生成される。すなわち、次が成り立つ。
L = RL u

証明

略■
 このとき、比
a
u
 ∈ RL
をaの単位uに関する測定値あるいは座標ざひょう, coordinateといいます。
 単位を定めて線分の長さを測ること、すなわち測定法は次の測定写像で表現することができます。
u-1 : L = RL u longrightarrow RL,  a =
a
u
 u longmapsto u-1(a) =
a
u
線分aを基底uで座標表現し、その座標に対応させる写像です。測定写像はRL-線形形式です。すなわち、次が成り立ちます。
         u-1(a + b)
=
u-1(a) + u-1(b),  a,b ∈ L
u-1(
s
t
a )
=
s
t
u-1(a),  a ∈ L,
s
t
 ∈ RL
 線長量Lの順序加群としてのノルム
 
:L longrightarrow L+, a longmapsto
a
は次のように定義されました。
a
 = lc96
a,
a
∈
L+
0,
a
=
0
-a,
a
∈
L-
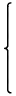 線長量上のノルムは比例倍を保存する性質がありますので、それを含めてノルムの性質としてまとめておきます。

命題1.8.2.9 線長量上のノルムの性質

線長量Lのノルムについて次が成り立つ。
(正値性) a ≧ 0かつa = 0 ⇔ a = 0,  a ∈ L
(比例倍) λ a = λ a,  λ ∈ RL, a ∈ L
(三角不等式) a + b ≦ a + b,  a,b ∈ L

証明

略■
 単位u ∈ L+を定めたときに、線長量のノルムに単位uによる測定写像を合成すると
 
:L longrightarrow RL+, a longmapsto
a
u
測定値の絶対値となり、これも上のノルムの性質を満たします。単位を定めたときにはこれをノルムと考えることにしましょう。これは通常のノルム概念と一致します。

定義1.8.2.12 単位をもつ線長量上のノルム

線長量Lにおいて単位u ∈ L+を定めるとき、そのノルムを順序加群としてのノルムに単位uによる測定写像を合成したものと定める。
a
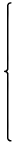 = lc144
a
u
,
a
∈
L+
0,
a
=
0
-
a
u
,
a
∈
L-
 単位uによる測定写像を使うと平面E上の距離
d : E × E longrightarrow L+,  (P,Q) longmapsto d(P,Q)
を
du : E × E longrightarrow RL+,  (P,Q) longmapsto du(P,Q)
du(P,Q) := lc96
[PQ]
u
P ≠ Q のとき
0
P = Q のとき
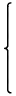と書くことができます。これは通常の距離概念と一致します。
 φ:L → RLを任意のRL-線形形式とし、
a
b
 := φ(u)
とおくと
φ(
s
t
u ) =
s
t
φ(u) =
s
t
a
b
ですから、
v :=
b
a
u
とおくとφ = v-1が成り立ちます。このことからL*でL上の線形形式全体の集合を表すと
L* = { u-1 | u ∈ L }
と書くことができることがわかります。言い換えれば、単位と測定法は一対一に対応しています。
 次に測定対象となる線分a ∈ Lを固定して、いろいろな測定法で測ってみることを考えましょう。これは次の写像で表現することができます。
a : L* longrightarrow RL,  u-1 longmapsto u-1(a) =
a
u
L*は自然にRL-線形空間となり、これをLの双対空間そうついくうかん, dual spaceと呼んでいます。この写像はRL-線形形式であり、さらにすべてのL*上のRL-線形形式はこの形で得られることから、
L ≅ (L*)*
であることがわかります。この性質をLとL*の双対性そうついせい, dualityといいます。
1.8.3 参考文献
[1] 小島 順, "量の計算"を見直す, 数学セミナー, 1977.8～1978.1
数　　学
作用域 さよういき, operator domain
線形空間 せんけいくうかん, linear space
線形写像 せんけいしゃぞう, linear mapping
線形形式 せんけいけいしき, linear form
線形変換 せんけいへんかん, linear transformation
線形結合 せんけいけつごう, linear combination
線形独立 せんけいどくりつ, linearly independent
線形従属 せんけいじゅうぞく, linearly dependent
基底 きてい, basis
次元 じげん, dimension
生成 せいせい, generate
座標 ざひょう, coordinate
双対空間 そうついくうかん, dual space
双対性 そうついせい, duality
 
Published by SANENSYA Co.,Ltd.