1.6節比の公式集

著者:梅谷武
語句:交叉比, 合併, 分離, 反転, 同位比, 乱比例

第V巻の命題をなるべくそのままの形で定式化して証明する。

作成:2009-08-25
更新:2011-03-08

1.6 比の公式集

この節は無向量の比の公式集として使えるように、第V巻の命題を整理しながら、なるべくそのままの形で定式化して証明していきます。また一部について線長量の場合の例を図示しました。

命題1.6.2 (V-8)

無向量M⁺の元a,b,cについて次が成り立つ。

a ＞ b ⇒ a:c ＞ b:c, c:a ＜ c:b

証明

自然数mをm(a-b) ＞ cとなるようにとり、自然数nを(n+1)c ＞ mb ≧ ncとなるようにとると、

ma ＞ (n+1)c, mb ＜ (n+1)c

となり、a:c ＞ b:c, c:a ＜ c:bが成り立つ。■

命題1.6.4 (V-9)

無向量M⁺の元a,b,cについて次が成り立つ。

a:c ∝ b:c ⇒ a = b

c:a ∝ c:b ⇒ a = b

証明

a ≠ bならば、命題V-8よりa:c ∝ b:c, c:a ∝ c:bに矛盾。■

命題1.6.6 (V-10)

無向量M⁺の元a,b,cについて次が成り立つ。

a:c ＞ b:c ⇒ a ＞ b

c:a ＞ c:b ⇒ a ＜ b

証明

a:c>b:cならば自然数m,nが存在して

ma ＞ nc, mb ≦ nc

となるからma＞mbが成り立つ。このことからa>bがわかる。次も同様。■

命題1.6.8 (V-12)

無向量M⁺の元a,b,c,dについて次が成り立つ。

a:b ∝ c:d ⇒ a:b ∝ (a+c):(b+d)

証明

ma ⋛ nb ⇒ mc ⋛ nd

より

m(a+c) ⋛ n(b+d)

が導かれる。■

図1.6.10 同位項の和

命題1.6.11 (V-14)

無向量M⁺の元a,b,c,dにおいてa:b ∝ c:dならば次が成り立つ。

a ＞ c ⇒ b ＞ d

a = c ⇒ b = d

a ＜ c ⇒ b ＜ d

証明

a ＞ c ⇒ b ＞ dを示す。

a ＞ c

⇒

a:b ＞ c:b [命題V-8]

⇒

c:d ＞ c:b [仮定]

⇒

b ＞ d [命題V-10]

■

命題1.6.13 (V-15)

無向量M⁺の元a,bと任意の自然数mについて次が成り立つ。

a:b ∝ ma:mb

証明

m'a ⋛ n'b ⇒ m'ma ⋛ n'nb

■

二つの比が比例するとき、それらの前項対前項と後項対後項も比例しますが、この操作を交叉比こうさひをとるといいます。

命題1.6.16 (V-16)

無向量M⁺の元a,b,c,dについて次が成り立つ。

a:b ∝ c:d ⇒ a:c ∝ b:d

証明

任意の自然数m,nについて、命題V-15より、

ma:mb ∝ nc:nd

である。命題V-14より、

ma ⋛ nc ⇒ mb ⋛ nd

であるから、a:c ∝ b:dが成り立つ。■

図1.6.18 交叉比

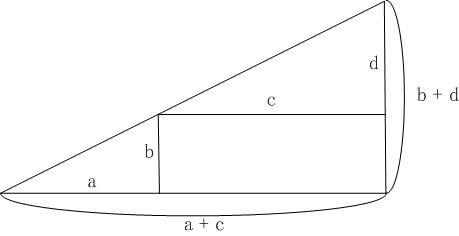
比の合併がっぺいとは前項と後項の和の後項に対する比をとることです。

命題1.6.20 (V-18)

無向量M⁺の元a,b,c,dについて次が成り立つ。

a:b ∝ c:d ⇒ (a+b):b ∝ (c+d):d

証明

ma ⋛ nb ⇒ mc ⋛ nd

より

m(a+b) ⋛ (m+n)b ⇒ m(c+d) ⋛ (m+n)d

■

図1.6.22 合併・分離・反転

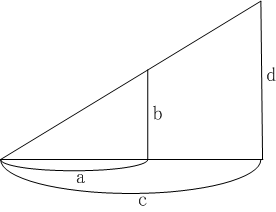
比の分離ぶんりとは合併された比を元に戻すことです。

命題1.6.24 (V-17)

無向量M⁺の元a,b,c,dについて次が成り立つ。

(a+b):b ∝ (c+d):d ⇒ a:b ∝ c:d

証明

m(a+b) ⋛ (m+n)b ⇒ m(c+d) ⋛ (m+n)d

より

ma ⋛ nb ⇒ mc ⋛ nd

■

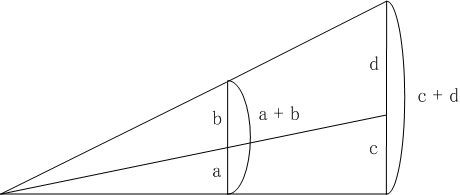
比の反転はんてんとは合併された比(a+b):bにおいて、前項の前項と後項の差に対する比(a+b):aをとることです。合併された二つの比が比例するとき、それらの反転も比例します。より一般的に次の命題が成り立ちます。

命題1.6.27 (V-19)

無向量M⁺の元a, b, c ＜ a, d ＜ bについて次が成り立つ。

a:b ∝ c:d ⇒ a:b ∝ (a - c):(b - d)

証明

a:b ∝ c:d

⇒

a:c ∝ b:d [命題V-16]

⇒

(a - c):c ∝ (b - d):d [命題V-17]

⇒

(a - c):(b - d) ∝ c:d [命題V-16]

■

命題1.6.29 (V-20)

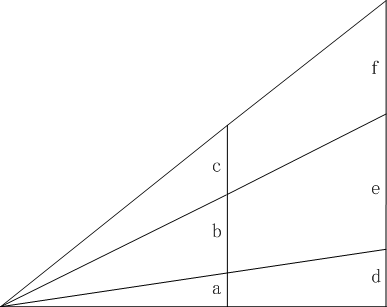
無向量M⁺の元の二つの列(a,b,c),(d,e,f)においてa:b ∝ d:e, b:c ∝ e:fならば次が成り立つ。

a ＞ c

⇒

b ＞ d

a = c

⇒

b = d

a ＜ c

⇒

b ＜ d

証明

a ＞ c ⇒ d ＞ fを示す。

a ＞ c

⇒

a:b ＞ c:b [命題V-8]

⇒

d:e ＞ f:e [仮定]

⇒

d ＞ f [命題V-10]

■

命題1.6.31 (V-21)

無向量M⁺の元の二つの列(a,b,c),(d,e,f)においてa:b ∝ e:f, b:c ∝ d:eならば次が成り立つ。

a ＞ c

⇒

b ＞ d

a = c

⇒

b = d

a ＜ c

⇒

b ＜ d

証明

a>c ⇒ d>fを示す。

a ＞ c

⇒

a:b ＞ c:b [命題V-8]

⇒

e:f ＞ e:d [仮定]

⇒

d ＞ f [命題V-10]

■

二組の同じ個数の無向量の列において、対応するどの二つの隣接項の比も比例するとき任意の同位項どうしの比も比例しますが、このような比を同位比どういひといいます。

命題1.6.34 (V-22)

無向量M⁺の元の二つの列(a,b,c),(d,e,f)においてa:b ∝ d:e, b:c ∝ e:fならばa:c ∝ d:fが成り立つ。

証明

命題V-4より、

ma:nb ∝ md:ne, nb:lc ∝ ne:lf

よって、命題V-20を(ma,nb,lc),(md,ne,lf)に当てはめれば、

ma ⋛ lc ⇒ md ⋛ lf

となり、定義よりa:c ∝ d:fである。■

図1.6.36 同位比

次の命題の仮定が満たされるとき、二組の三個の無向量の列は乱比例らんぴれいするといいます。

命題1.6.38 (V-23)

無向量M⁺の元の二つの列(a,b,c),(d,e,f)においてa:b ∝ e:f, b:c ∝ d:eならばa:c ∝ d:fが成り立つ。

証明

命題V-15より、

a:b ∝ ma:mb, e:f ∝ ne:nf

仮定からa:b ∝ e:fであるから、

ma:mb ∝ ne:nf

命題V-16よりb:c ∝ d:eの交叉比は等しい。

b:d ∝ c:e

命題V-15より、

b:d ∝ mb:md, c:e ∝ nc:ne

であるから、

mb:md ∝ nc:ne

よって、命題V-21を(ma,mb,md),(nc,ne,nf)に当てはめれば、

ma ⋛ nc ⇒ md ⋛ nf

となり、定義よりa:c ∝ d:fである。■

命題1.6.40 (V-24)

無向量M⁺の元a,b,c,d,s,tにおいてa:b ∝ c:d, s:b ∝ t:dならば(a+s):b ∝ (c+t):dが成り立つ。

証明

s:b ∝ t:dより、命題V-7系からb:s ∝ d:tである。 (a,b,s),(c,d,t)に命題V-22を適用すれば、

a:s ∝ c:t

となり、命題V-18より、

(a+s):s ∝ (c+t):t

であるから、((a+s),s,b),((c+t),t,d)に命題V-22を適用すれば、

(a+s):b ∝ (c+t):d

■

命題1.6.42 (V-25)

無向量M⁺の元a,b,c,dにおいてaが最大、dが最小であり、a:b ∝ c:dならばa+d ＞ b+cが成り立つ。

証明

交叉比a:c ∝ b:dに命題V-19を適用すれば、

a:c ∝ (a-b):(c-d)

ここで、a>cより(a-b)>(c-d)であり、順序半加群の計算法則により両辺にb+dを加えれば

a + d ＞ b + c

■

数　　学

交叉比こうさひ
合併がっぺい
分離ぶんり
反転はんてん
同位比どういひ
乱比例らんぴれい

Published by SANENSYA Co.,Ltd.