1.2節 公準と公理
著者:梅谷 武
語句:定義, 公準, 公理, 有向量, 無向量, 可差性, 可差半加群, 順序半加群, 閉包, アルキメデス性
語句:定義, 公準, 公理, 有向量, 無向量, 可差性, 可差半加群, 順序半加群, 閉包, アルキメデス性
原論の論証体系のあらまし、図形に関する公準、量に関する公理、無向量を特徴付けるの可差性とアルキメデス性について述べる。
作成:2009-08-20
更新:2011-03-08
更新:2011-03-08
原論は第I巻の冒頭で、定義ていぎ, definitionとして幾何の用語を日常的に使われる言葉で説明し、公準こうじゅん, postulateとして図形の性質に関する原則を、公理こうり, axiomにおいて量の性質に関する原則を列挙しています。原論のすべての命題の証明にはこの公準と公理が使われていますが、これら自身は原論の体系内において証明されることはありません。
原論の定義・公準・公理は現代数学のそれとは異なり、単に証明することができないものを大雑把に分類したような使われ方をしています。第II巻以降の冒頭にも定義がありますが、その中には公理や公準とした方がいいようなものもあります。例えば、第V巻の定義4はいわゆる「アルキメデスの公理」と呼ばれるもので、全体の流れからすると第I巻の量に関する公理の中に入れるのが適当です。これが第V巻の冒頭にあるのは、原論が長い時間をかけ、多くの人の仕事が編集されて成立したという事情によるものと思われます。これはエウドクソスEudoxus, 前390頃-前337頃が比例論を構築するに当たって必要になった公理を冒頭で追加したものと想像されます。
公準1.2.2.1 (公準1)
任意の点から任意の点へ直線を引くことができる。 平面上の任意の場所に二点が与えられたときに、その二点を結ぶ直線を引くことができるというものです。我々は図形を点の集合と考えていますから、これは直線が平面の部分集合になっていることも含んでいます。これは平面に距離を導入することを可能にするものですので、次のように言い換えておきます。
公準1.2.2.3 (公準1')
任意の点から任意の点へ直線を引くことができ、その直線の長さが二点間の距離である。 より精密な議論のために記号を導入します。平面上の二点A,Bについて、始点Aと終点Bを結ぶ直線をABで表します。同じように始点をB、終点をAとする直線はBAと書かれますが、これらは線分としては同じと考えます。記号で表せばAB = BAとなります。
次章で導入される有向線分の場合は同じ二点A,Bを結ぶ直線でも、始点と終点を区別してAB ≠ BAとなります。直線について方向を考えない場合、特に有向線分と区別したいときに無向線分むこうせんぶん, undirected segmentと呼ぶことにします。
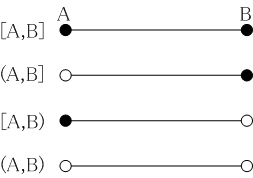
無向線分においても始点Aと終点Bは位置として異なりますから、位置の違いが問題になるときや、線分を領域として扱うことを強調したいときは、始点Aと終点Bを結ぶ直線を[A,B]と書き、さらに[A,B]から端点Aを除いた点集合を(A,B]、[A,B]から端点Bを除いた点集合を[A,B)、[A,B]から両端点A,Bを除いた点集合を(A,B)と書くことにします。
次の公準は平面が無限に広がっていることを要請するものです。
公準1.2.2.9 (公準2)
任意の直線は、どちらの方向にもいくらでも伸ばすことができる。 これは平面上に距離が導入された段階で、次のように言い換えることができます。
公準1.2.2.11 (公準2')
平面上の無限直線は有界ではなく、直線上の任意の点を中心とする円と必ず二点で交わる。 次の公準は、中心点とそれを端点とする直線を与えれば、それを半径とする円が描けることを要請するものです。これは直線を自由に回転させることができることも意味しています。
公準1.2.2.13 (公準3)
任意の中心と任意の半径の円を描くことができる。 これは命題I-2の「与えられた直線と同じ長さの直線を与えられた点から作図すること」とは主張している内容が異なることに注意してください。原論の公準では、中心点とそれを始点とする直線である半径を与えなければ円を描くことができません。命題I-2によって初めてコンパスのように自由に半径を調整して円を描くことができるようになっています。
次の公準はヒルベルトも指摘しているように角を半直線に囲まれた領域と定義する立場では、命題として証明することができます。
公準1.2.2.16 (公準4)
すべての直角は互いに等しい。 最後は有名な平行線公準です。
公準1.2.2.18 (公準5)
二つの直線と交わる直線の同じ側の内角の和が二直角より小さいならば、二つの直線を同じ側に伸ばしていけばいつかは交わる。 ここで平行の概念を導入しておきましょう。
定義1.2.2.20 (I-23)
平行へいこう, parallelな直線とは、同じ平面上にある複数の直線でどちらの方向にどれだけ伸ばしても交わることのないものである。 平行線公準はその後の研究によって、「任意の直線とその直線上に無い
任意の点を与えたとき、その点を通り、与えられた直線に平行な直線は
唯一つ存在する」という命題と同等であることがわかっています。
原論では、二つの図形を比較して、等しい、大きい、小さいという関係性について論ずることがその主な目的の一つになっています。geometryはギリシャ語のγεωμετρίαが英訳されたものですが、これは土地(geo)を測ること(metry)に由来しています。これを文字通り日本語に訳せば測地学あるいは測量学となります。
以下、量を比較するための原理として与えられている公理について解説していきます。この量に関する公理群によって、量に代数構造が導入されることになります。
原論において、二つの図形、例えば三角形が等しいといったときに、合同か、あるいは面積が等しいかの二種類の意味があります。また直線が等しいといったときにはその長さが等しいことを意味しますが、同じ長さの直線でも位置や方向を考える場合は別のものとして取り扱わなければなりません。このようにある二つの物を比較して等しいという場合には、その意味に誤解が生じないようにしなければなりません。
ある性質をもった図形全体の集合を考えます。これは例えば、Line = {平面上の線分全体}、Area = {平面上の直線図形全体}というようなものです。原論における量りょう, quantityとは、このような集合に含まれる二つの図形が「等しい」という恒等概念や「大きい」「小さい」という順序関係を導入して、その図形集合を分類しようとするものです。この「等しい」という恒等概念に要求される性質を最初の公理が表しています。
公理1.2.4.3 (公理1)
同じものに等しいものは互いに等しい。 これはある種の図形全体の集合において二つの図形が等しいという関係が同値関係になっていると解釈することができます。
定義1.2.4.5 同値関係
集合における任意の二元の関係∼が次の性質を満たすとき、同値関係どうちかんけい, equivalence relationという。| (反射律) | 任意の元aについてa ∼ a |
| (対称律) | 任意の二元a,bについてa ∼ b ⇒ b ∼ a |
| (推移律) | 任意の三元a,b,cについてa ∼ b, b ∼ c ⇒ a ∼ c |
公理1.2.4.6 (公理1')
量とは図形の同値類のことである。 例えば Line において、公準で許された作図によって互いにぴったり重なり合うという関係∼は同値関係になります。このとき互いに同値な元をすべて集めて Line の部分集合を作ります。このような部分集合の全体の集合を考えると、どの部分集合どうしも交わりがなく、なおかつそれらすべてを合併すると Line になります。このように同値関係は集合を分割します。これを集合の類別といい、各部分集合を同値類と呼びます。同値類全体の集合を商集合といい、Line/∼と書きます。このとき商集合L+ := Line/∼を長さという量の集合であると考えるわけです。
今後、L+を線長量せんちょうりょうと呼ぶことにして、線分の等長類すなわちL+の元を英小文字でaのように記し、線分すなわち Line の元をギリシア小文字でαのように記すことにします。aがα=ABを含む場合、
あるいは
と表し、α=ABはaの代表元であるといいます。
| α = AB ∈ a |
| a = [α] = [AB] |
このとき、自然に線分ABに対してその同値類である長さ[AB]を対応させる写像が定まります。
| Line |
説明の都合上、公理2,3と公理4,5の順番を入れ替えます。
公理1.2.5.2 (公理2)
重ね合わせることができるものは互いに等しい。公理1.2.5.3 (公理3)
全体は部分より大きい。 これは平面図形が作図によってぴったり重ね合わせることができれば等しいとみなし、重ね合わせたときに領域として包含関係が生ずるときに、それによって大小を決めるという比較原理について述べています。
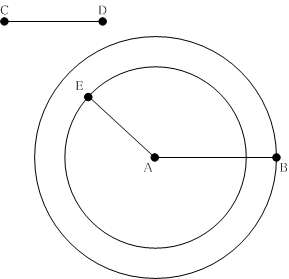
まず、直線の場合を考えてみましょう。二つの線分AB,CDが与えられたとすると、命題I-2「与えられた直線と同じ長さの直線を与えられた点から作図すること。」により、CD ∼ AEなる線分AEを引くことができます。公準3より、Aを中心とし半径ABの円と半径AEの円を描くことができますが、このとき、次の三通りの場合が考えられます。
| (1) | 半径ABの円と半径AEの円が一致する。 |
| (2) | 半径ABの円の内部に半径AEの円が含まれる。 |
| (3) | 半径AEの円の内部に半径ABの円が含まれる。 |
(1)の場合、円の定義からABとAEの長さは等しく、[AB] = [CD]となります。(2)の場合、半径AEの円とABの交点E'が存在し、AE ∼ AE'となり、[AE'] ⊂ [AB]ですから、[AB] > [CD]となります。(3)の場合、半径ABの円とAEの交点B'が存在し、AB ∼ AB'となり、[AB'] ⊂ [AE]ですから、[AB] < [CD]となります。
このようにして、線長量Lに平面上の領域としての包含関係と一致する順序を定めることができます。これは次の意味で順序関係であり、さらに全順序になっています。
定義1.2.5.9 順序関係
集合における任意の二元の関係≦が次の性質を満たすとき、その関係を順序じゅんじょ, orderという。| (反射律) | 任意の元aについてa ≦ a |
| (反対称律) | 任意の二元a,bについてa ≦ b, b ≦ a ⇒ a=b |
| (推移律) | 任意の三元a,b,cについてa ≦ b, b ≦ c ⇒ a ≦ c |
| (全順序) | 任意の二元a,bについてa ≦ bまたはb ≦ a |
a ≦ bかつa ≠ bのときa < b、a ≧ bかつa ≠ bのときa > bと書くことにします。
公理1.2.5.11 (公理2')
二つの図形を平面上の領域として等しくできるならば量として等しい。公理1.2.5.12 (公理3')
二つの図形に平面上の領域として包含関係をもたせることができれば、それは量としての順序関係になる。 この量の比較原理は線長量L+にはうまく適用できますが、広がりをもった直線図形においてはこれだけではうまくいきません。領域としての包含関係をうまくもたせることができない場合でも、量としての恒等性あるいは大小関係について論ずることが必要になってきます。原論においては、等積変形により一辺を共通にもつ長方形にする方法、正方化する方法、相似な図形の一辺の比を比較する方法の三種類の方法によって面積を比較しています。これについては後の面積論において論じます。
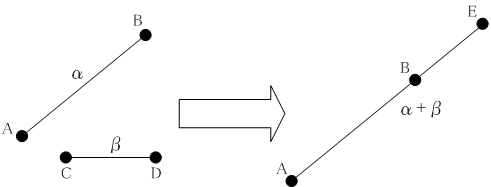
公準2「任意の直線は、どちらの方向にもいくらでも伸ばすことができる」と命題I-2「与えられた直線と同じ長さの直線を与えられた点から作図すること」によって、任意の二つの線分を継ぎ足して新しい線分を作図することができます。
線分α=AB, β=CDが与えられたときに、AからBへ向かう方向へ点Eをとり、[A,B] ⊊ [A,E]かつ[B,E] ∼ [C,D]とすることができます。このときα + β = AB + CD := AEによって線分の和を定義します。
同じようにCからDへ向かう方向へ点Fをとり、[C,D] ⊊ [C,F]かつ[D,F] ∼ [A,B]とすることができて、β + α = CD + AB := CFとなります。
次の公理は線分の和が長さの和を引き起こすことを要請するものです。
公理1.2.6.6 (公理4)
等しいものに等しいものを加えた和は互いに等しい。 これはα ∼ α', β ∼ β'ならばα + β ∼ α' + β'、すなわち、線分の和は同じ長さの同値類の代表の取り方によらずに定まることを意味しています。これにより長さの和を[α] + [β] := [α+β]と定義することができます。
これは次の可換図式で表現されます。
|
さらに量は加法に関して可換律と結合律を満たします。
定義1.2.6.10 半加群
集合Sの二つの元a, bについて加法a+b ∈ Sが定義されていて次の性質を満たすとき、Sは半加群はんかぐん, semi-moduleであるという。| (可換律) | 任意の二元a,bについて、a + b = b + a |
| (結合律) | 任意の三元a,b,cについて、(a + b) + c = a + (b + c) |
| (零元) | 0 ∈ Sが存在し、任意の元aについて、a + 0 = 0 + a = a |
公理1.2.6.11 (公理4')
量は加法に関して半加群となる。 線分の和が半加群の性質を満たすことは作図によって証明することができます。Lineには始点と終点が一致する線分、すなわち点は含まれないものとします。したがって、L+には零元が含まれません。これは次に述べる無向量にも当てはまります。
線分を量として考えるときに、長さだけでなく方向を加味した有向量ゆうこうりょう, vectorまで考えることができます。原論では方向についても考慮していますが、これを量として代数的に扱うことはありません。原論が代数的に扱っているのは長さや広さのような無向量むこうりょう, scalarに限られています。量が半加群をなすことについては、無向量も有向量も同じですが、ここで議論する可差性は無向量だけがもつ特別な性質です。
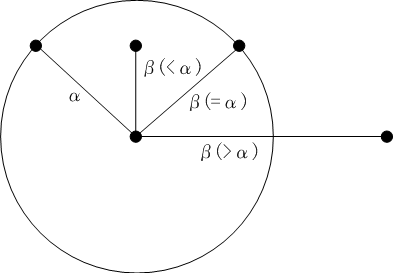
命題I-3「長さが異なる二つの直線が与えられたとき、長い方から短い方の長さを切り取ること」の証明の手法を利用すると、二つの線分α,βが与えられたとき、αとβの関係は下図の三通りのいずれかになることがわかります。
αがβより長いとき、α = β + γなる線分γを作図することができます。これをγ = α - βと書きます。βがαより長いとき、β = α + γなる線分γを作図することができます。これをγ = β - αと書きます。
公理1.2.7.5 (公理5)
等しいものから等しいものを引いた差は互いに等しい。 これはα ∼ α', β ∼ β'であり、α = β + γなるγが存在し、α' = β' + γ'なるγ'が存在するとき、γ ∼ γ'あるいはα - β ∼ α' - β'と書くことができます。すなわち、線分の差は同じ長さの同値類の代表の取り方によらずに定まることを意味しています。これにより[α] - [β] := [α-β]によって長さの差を定義することができます。
一般に半加群に順序や減法を導入することを可能にするこの性質を次のように定義します。
定義1.2.7.8 可差半加群
半加群の任意の二元a,bについて、次のいずれか一つが成り立つとき、可差性かさせい, differentiabilityをもつといい、このような半加群を可差半加群かさはんかぐん, differentiable semi-module という。| (1) | a = b + cなるcが存在する。 |
| (2) | a = b |
| (3) | b = a + cなるcが存在する。 |
可差半加群において、
と定めると順序になります。これにより可差半加群は全順序集合となり、次のような強い性質をもちます。
| (1) or (2) ⇒ a ≦ b | |
| (2) or (3) ⇒ a ≧ b |
命題1.2.7.10 可差半加群における順序の単調性
可差半加群の順序には次の性質がある。| (単調性) | 任意の三元a,b,cについてa < b ⇒ a + c < b + c |
証明
a=b+rとするとa+c=(b+r)+c=b+(r+c)=b+(c+r)=(b+c)+rであるからa + c < b + c。■定義1.2.7.12 順序半加群
単調性がある順序をもつ半加群を順序半加群じゅんじょはんかぐん, ordered semi-moduleという。 順序半加群では次のような計算法則が成り立ちます。
命題1.2.7.14 順序半加群の計算法則
順序半加群において、次が成り立つ。| (1) | 任意の四元a,b,c,dについてa < b, c < d ⇒ a + c < b + d |
| (2) | 任意の三元a,b,cについてa = b ⇔ a + c = b + c |
| (3) | 任意の三元a,b,cについてa < b ⇔ a + c < b + c |
証明
(1) 定義より、a + c < b + c, c + b < d + b。(2) ⇒は集合の元として同じものを別の記号で表していることから。
⇐はa < b, b < aのどちらを仮定しても単調性より矛盾が生ずることから。
(3) ⇒は定義より。⇐はb < aを仮定すると単調性より矛盾が生じ、a = bを仮定すると(4)より矛盾が生ずることから。■
上の(2) ⇐の性質は加法における簡約律と呼ばれますが、これにより差の一意性が導かれます。
ここまでの議論で可差半加群においては減法が定義できることがわかりました。簡約律が成り立ち、減法が定義されると移項ができるようになります。すなわち、a < b, a > cのとき次が成り立ちます。
| a = b + c ⇔ a - c = b |
可差半加群は定義から零元をもつことができませんが、順序半加群として零元を付加することができます。
命題1.2.7.20 可差半加群の閉包
零元をもたない順序半加群Nに0を付け加えた集合N := N ∪ {0}について、- a + 0 = 0 + a = a, a ∈ N
- a > 0, a ∈ N
証明
略。■ 可差性の他にもう一つ重要な性質があります。それはエウドクソスによるとされる第V巻の冒頭で定義4として述べられ、アルキメデスArchimedes, 前287頃-前212がよく使ったことから現代では慣例として「アルキメデス的」と呼ばれている性質です。
定義1.2.8.2 V-4
順序半加群の元aと自然数nについて、| na := a + ⋯ + a (n個の和) |
これにより次のように公理を言い換えておきます。
公理1.2.8.4 (公理5')
無向量はアルキメデス的可差半加群である。人 物
エウドクソス Eudoxus, 前390頃-前337頃アルキメデス Archimedes, 前287頃-前212
数 学
定義 ていぎ, definition公準 こうじゅん, postulate
公理 こうり, axiom
無向線分 むこうせんぶん, undirected segment
平行 へいこう, parallel
量 りょう, quantity
同値関係 どうちかんけい, equivalence relation
線長量 せんちょうりょう
順序 じゅんじょ, order
全順序 ぜんじゅんじょ, total order
半加群 はんかぐん, semi-module
有向量 ゆうこうりょう, vector
無向量 むこうりょう, scalar
可差性 かさせい, differentiability
この文脈で可微分性が論じられることはないので暫定的な英訳としてこの語を割り当てた。
可差半加群 かさはんかぐん, differentiable semi-module順序半加群 じゅんじょはんかぐん, ordered semi-module
閉包 へいほう, closure
アルキメデス的 あるきめですてき, Archimedean
Published by SANENSYA Co.,Ltd.