1.10節角度論

著者:梅谷武
語句:余弦, 正弦, 正接, 三角法, 円周率, 弧度法, 三角関数

ピュタゴラスの定理の拡張、三角法、弧度法について述べる。

作成:2009-08-28
更新:2021-03-21

1.10 角度論

1.10.1 ピュタゴラスの定理の拡張

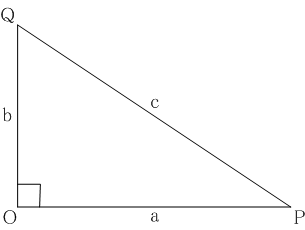
第I巻命題I-47はいわゆるピュタゴラスPythagoras, 前572頃-前494頃の定理です。

命題1.10.1.2 I-47

直角三角形において、直角に対する辺上の正方形は直角を挟む辺上の正方形の和に等しい。

図1.10.1.3 命題I-47

これは平面上の点Oを始点とする線分OPと線分OQが直交するとき、線長量a = [OP], b = [OQ],c = [PQ]の間に

c ⊗ c = a ⊗ a + b ⊗ b

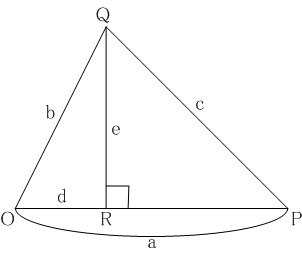
という面積量の関係式が成り立つことを意味しています。第II巻ではこれが拡張されます。命題II-12は鈍角三角形の場合です。

命題1.10.1.5 II-12

鈍角三角形において、鈍角に対する辺上の正方形は、鈍角を挟む二辺上の正方形の和より、鈍角を挟む一つの辺とその辺の延長へ下ろされた垂線までの延長部分によって定まる長方形の二倍だけ大きい。

これは平面上の点Oを始点とする線分OPと線分OQのなす角∠ POQが鈍角であるとき、QRをQからOPをPからOへ向かう方向へ延長した直線上へ下ろした垂線としたとき、線長量a = [OP], b = [OQ], c = [PQ], d = [OR]の間に

c ⊗ c = a ⊗ a + b ⊗ b + 2 ( a ⊗ d )

という面積量の関係式が成り立つことを意味しています。

図1.10.1.7 命題II-12

原論の証明は、e = [QR]としたとき、

(a+d) ⊗ (a+d) = a ⊗ a + d ⊗ d + 2 (a ⊗ d)

の両辺にe ⊗ eを加えると、ピュタゴラスの定理により、左辺はc ⊗ cに等しく、右辺におけるd ⊗ d + e ⊗ eはb ⊗ bに等しいので求める関係式が成り立つ、となっています。

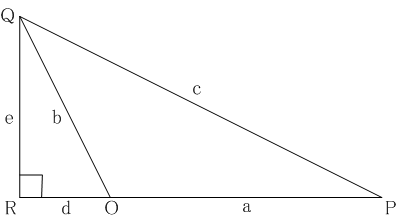
命題II-13は鋭角三角形の場合です。

命題1.10.1.10 II-13

鋭角三角形において、鋭角に対する辺上の正方形は、その鋭角を挟む二辺上の正方形の和より、鋭角を挟む一つの辺とその辺へ下ろされた垂線により分割される部分によって定まる長方形の二倍だけ小さい。

これは平面上の点Oを始点とする線分OPと線分OQのなす角∠ POQが鋭角であるとき、QRをQからOP上へ下ろした垂線としたとき、線長量a = [OP], b = [OQ], c = [PQ], d = [OR]の間に

c ⊗ c = a ⊗ a + b ⊗ b - 2 (a ⊗ d)

という面積量の関係式が成り立つことを意味しています。

図1.10.1.12 命題II-13

原論の証明は、命題II-7「直線が任意に分割されるとき、全体の直線上の正方形と一つの部分上の正方形の和は、全体とその部分が定める長方形の二倍と残りの部分上の正方形の和に等しい。」を使って、

d ⊗ d + a ⊗ a = 2 (a ⊗ d) + (a - d) ⊗ (a - d)

を導き、e = [QR]とおいて両辺にe ⊗ eを加えるとピュタゴラスの定理により、右辺における(a-d) ⊗ (a-d) + e ⊗ eはc ⊗ cに等しく、左辺におけるd ⊗ d + e ⊗ eはb ⊗ bに等しいので求める関係式が成り立つ、となっています。

1.10.2 三角法

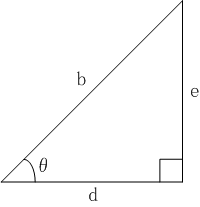
ピュタゴラスの定理を鈍角あるいは鋭角に拡張するとき、

2(a ⊗ d)

という面積量は正方形の和の過不足を補うものです。ここでdという線長量は線長比b:dを使って

d =

と書くことができます。この比は角∠ POQによって定まり、線長量bには依存しません。この比のことを余弦よげん, cosineといいます。同じように角度によってのみ定まる線長比b:eを正弦せいげん, sine、線長比d:eを正接せいせつ, tangentといいます。角度をθで表わしたとき、正弦をsin θ、余弦をcos θ、正接をtan θと書きます。

古代ギリシアの天文学者アリスタルコスAristarchus, 前310頃-前230頃は、『太陽と月の大きさと距離について』という著作において、地球から太陽と地球から月までの距離の比や、太陽、月、地球の直径の比などを求めています。このように角度を直角三角形の辺の比で表して測量や天文学に応用する方法は三角法さんかくほう, trigonometryと呼ばれています。

sin θ

cos θ

tan θ

この記法を使うと

a ⊗ d = cos θ a ⊗ b

と書くことができますが、この面積量は角度θと線長量a,bの両方の要素を一度に合わせて表現できる便利なもので、後に二つのベクトルの関係性を測る内積へと拡張されることになります。

1.10.3 弧度法

原論における円の面積に関する主張は、命題XII-2「円は直径上の正方形に比例する。」にとどまりますが、エウクレイデスが原論を編纂した時期より少し後に、アルキメデスArchimedes, 前287頃-前212が『円の測定』において、次の命題を取尽し法によって証明しています。

定理1.10.3.2 アルキメデス

円は半径と円周と同じ長さの線分が直角を挟む辺となるような直角三角形に等しい。

証明

略■

アルキメデスの証明は原論の体系を踏襲していますので、原論を継承・発展させたものと認めることにし、円周や円弧の長さはアルキメデスの議論において定義されるものとします。

二つの円の半径をr₁, r₂、円周をl₁, l₂とし、面積の双線形を使うと

r₁ ⊗ r₁ : r₁ ⊗ l₁

∝

r₂ ⊗ r₂ : r₂ ⊗ l₂

r₁ ⊗ r₁ : r₁ ⊗

l₁

r₁

∝

r₂ ⊗ r₂ : r₂ ⊗

l₂

r₂

r₁ ⊗ r₁ :

l₁

r₁

(r₁ ⊗ r₁)

∝

r₂ ⊗ r₂ :

l₂

r₂

(r₂ ⊗ r₂)

r₁ : l₁

∝

r₂ : l₂

となり、円周が半径に比例することがわかります。

系1.10.3.6

円周は直径に比例する。

以後、円の直径と円周の線長比を円周率えんしゅうりつ, circle ratioと呼び、πで表すことにします。

図1.10.3.8 弧度法

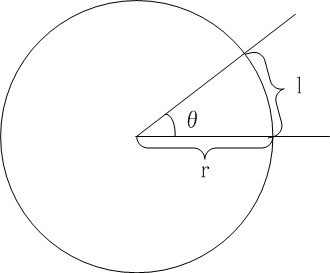
角θが与えられたとき、その頂点を中心とする半径rの円を描き、その円と角θの領域との交線である円弧をlとします。このとき、円周が直径に比例することと同じ論法によって同じ角度を挟む円弧が直径に比例することが証明できます。

系1.10.3.10

同じ角度を挟む円弧は直径に比例する。

したがって、角θによって定まる線長比r:lは半径rのとり方によらずに定まります。角度をこのようにして定まる線長比によって表現する方法を弧度法こどほう, circular methodといいます。弧度は直角を∠Rで表すとき、4∠Rが円周率πで表されることを利用して、πを基準にして表現されます。

↔

∠R

↔

2∠R

↔

4∠R

↔

2π

1.10.4 回転量

1.1節において角度は半直線の組によって囲まれた領域であると定義しました。しかし、命題I-23『与えられた直線上に、与えられた直線角を作図すること。』により、二つの角度の加法を定義すると和が一回転を超えてしまうという問題が起こります。これは直角を∠Rで表すことにすると、和が4∠Rを超える場合があるということです。

このため角度そのものではなく、角度を定める半直線の回転の度合いを量W⁺として考えます。そうするとWはアルキメデス的可差半加群となり、代数的には線長量L⁺や面積量A⁺と同じ構造を持ちます。W⁺を対称化したものをWと書くことにしましょう。

図1.10.4.3 回転量

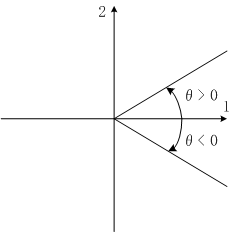
角度を回転量に対応させるために、まず角度を定める半直線の一方を平面の正規直交基底の最初の軸の原点から正方向に合わせます。もう一方の半直線が反時計回りに回転する方向を正、その逆の時計回りに回転する方向を負と定めます。こうすると回転量Wの区間[0,4∠R)が図形としての角度と一対一に対応します。

正弦sin θ、余弦cos θ、正接tan θは回転量Wから線長比R_Lへの関数と考えることができます。これらを三角関数さんかくかんすう, trigonometric functionと呼びます。区間[0,4∠R)内については角度としての線長比をとり、区間外の回転量θについては

θ + 4n∠R ∈ [0,4∠R)

なる整数nを求めて対応する角度の線長比をとるようにします。この定義から三角関数は4∠Rを周期とする周期関数になることがわかります。

後で必要になる三角関数の公式をまとめておきます。

命題1.10.4.7 三角関数の公式

θ,α,β ∈ Wについて次が成り立つ。

sin² θ + cos² θ = 1

sin (-θ) = -sin θ

cos (-θ) = cos θ

sin ( θ + ∠R ) = cos θ

(1.8)

cos ( θ + ∠R ) = -sin θ

(1.9)

sin ( θ + 2∠R ) = -sin θ

(1.10)

cos ( θ + 2∠R ) = -cos θ

(1.11)

sin ( α + β ) = sin α cos β + cos α sin β

(1.12)

sin ( α - β ) = sin α cos β - cos α sin β

(1.13)

cos ( α + β ) = cos α cos β - sin α sin β

(1.14)

cos ( α - β ) = cos α cos β + sin α sin β

証明

略■

回転量Wも一次元線形空間になります。

命題1.10.4.10

回転量Wは線長比R_L上の一次元線形空間であり、直角∠Rを単位と定めると次のように表すことができる。

W = R_L ∠R

証明

略■

回転量を弧度法で表すこともできます。この場合は三角関数は線長比R_Lから線長比R_Lへの関数であり、2πを周期とする周期関数になります。三角関数を角度で表すか弧度法で表すかはそのときの文脈で決めるものとします。

1.10.5 参考文献

[1] 上垣渉, アルキメデスを読む, 日本評論社, 1999

[2] 上垣渉, はじめて読む数学の歴史, 角川学芸出版, 2016

人　　物

ピュタゴラス Pythagoras, 前572頃-前494頃
アリスタルコス Aristarchus, 前310頃-前230頃
アルキメデス Archimedes, 前287頃-前212

数　　学

余弦よげん, cosine
正弦せいげん, sine
正接せいせつ, tangent
三角法さんかくほう, trigonometry
円周率えんしゅうりつ, circle ratio
弧度法こどほう, circular method
三角関数さんかくかんすう, trigonometric function

Published by SANENSYA Co.,Ltd.