1.1節 平面幾何の構成要素
著者:梅谷 武
語句:点, 線, 直線, 面, 平面, 図形, 角, 円
語句:点, 線, 直線, 面, 平面, 図形, 角, 円
点, 線, 円等の平面幾何の構成要素を定義する。
作成:2009-08-19
更新:2021-03-21
更新:2021-03-21
「点(點,テン,会意・形声)」は占いで場所を示すための黒いしるしのことを意味しています。「卜(ボク,象形)」は亀の甲を焼いたときの割れ目を描いたものでうらないを意味し、物や場所を示す「口」を付けて、卜によって物や場所を選ぶ「占(セン,会意)」となりました。「黑(黒,コク,会意)」の下部は火を、上部は煙突に点々とすすがついたさまを表しています。「點」は後に略されて「点」となりました。
幾何においては、位置という概念の究極の形態、まさに位置そのものであるものを意味し、長さ、広がりや厚さなどいかなる意味でも大きさをもちません。したがって、それを分割することはできません。ここでは幾何の考察の対象となるすべての図形は点の集合であると考えます。
原論では次のように定義しています。
定義1.1.1.4 (I-1)
点てん, pointとはそれ以上分割できないものである。 作図する際には、筆を使って平面上の任意の場所に点を打つことができます。本来、点には大きさがありませんが、図で象徴的に示すときは小さな黒い丸を使います。
「線(綫,セン,会意・形声)」は岩穴から一筋わきだす泉のような糸のように細長いものを意味します。「泉(セン,象形)」は丸い穴から水が湧き出る様を描いています。両刃の剣に鳶口のように直角に長い柄をつけて敵を引っ掛けるように使った武器である「戈(ほこ,象形)」を二つ並べた「戔(セン,会意)」は、刃物で削りに削って残りが少ないことを意味し、それに糸をつけた「綫(セン,会意・形声)」は細い糸を表します。後に「線」が有力となりました。
幾何においては、点を運動させたときの軌跡のことを意味します。
線を作図するには筆先を平面上に付けたまま運動させます。筆先は広がりをもたないのでその軌跡である線も広がりをもつことはありません。運動を開始したときの点である始点してん, starting pointと終了したときの点である終点しゅうてん, end pointをその線の端点たんてん, edge pointといいます。
原論では次のように定義しています。
定義1.1.2.6 (I-2)
線せん, lineとは長さをもち、幅をもたないものである。定義1.1.2.7 (I-3)
線の端はし, edgeは点である。 一般に平面上にある点の集合を領域りょういき, domainと呼びます。領域が連結れんけつ, connectedであるとは、領域に含まれる任意の二点に対して、それらを結ぶ線で、その線に含まれている点がすべて領域に含まれるようなものが存在するときのことをいいます。任意の線は領域と考えると連結です。
端点は線からその点を除いた領域が連結であるような点として特徴付けることができます
「直(チョク,象形)」は上にまじないの印をつけた目の象形で、まっすぐ見つめることを意味しています。
定義1.1.3.2 (I-4)
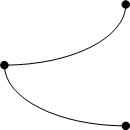
直線ちょくせん, straight lineとは点がまっすぐに並んだ線である。 原論ではまっすぐであるということはどういうことなのかについては説明していませんが、ここでは線を作図するときの筆の運動の方向が一定であることを意味するものとします。二点間を結ぶ直線には最短線という重要な性質があり、これにより距離としての機能を果たすことになります。「直」という字の意味から、物理光学的に直線とは平面上のある方向から見たときに見えなくなる線のことであると解釈することもできるでしょう。
現代ではこの図のような有限の長さの直線を線分せんぶん, segmentと呼び、直線という言葉を無限に長い直線のこととして扱うことが一般的ですが、原論では線分を直線と呼び、無限に長い直線を無限直線むげんちょくせん, infinite lineと呼んでいます。ここでは線分や直線を有限か無限かの違いをはっきり区別する必要があるときに、線分あるいは無限直線という言葉を用い、そうでないときには直線ということにしましょう。
「面(メン,指事)」は、人の頭部を表わす象形を、顔の輪郭を示す「口」で囲んで人の顔を表わします。幾何においては、線に囲まれた領域を意味します。
定義1.1.4.2 (I-5)
面めん, surfaceとは長さと広さをもち、容積をもたないものである。定義1.1.4.3 (I-6)
面の端は線である。 面は空間内の立体的な図形の表面という意味で使われ、曲面も含んでいます。平面幾何といっても三次元的な空間内で考えています。
「平(ヘイ,象形)」は浮き草が水面にたいらに浮かんだ姿を描いています。平面とは限りなく広がる平らな面のことです。
定義1.1.5.2 (I-7)
平面へいめん, plain surfaceとは直線が平らに並んだ面である。 「図(圖,ズ,会意)」は米倉の象形である「啚」を「口」で囲んで耕作地の境界を表します。「形(ケイ,会意・形声)」は、かたやわくを意味する象形で音符の「井(ケイ)」と模様を表す「彡」を合わせてかたちを表します。
図形は境界に囲まれた領域として定義されます。
定義1.1.6.3 (I-13)
境界きょうかい, boundaryとは何かの端である。定義1.1.6.4 (I-14)
図形ずけい, figureとは一つあるいは複数の境界に囲まれたものである。 直線を固定してその中だけの世界を考えれば、その直線内の二つの点を結ぶ直線はその二点を境界とする図形です。いいかえれば線分では二つの端点が境界になっています。平面を固定してその中だけの世界を考えれば、その平面内の線に囲まれる領域は、その線を境界とする図形です。空間内で面に囲まれる領域は、その面を境界とする図形です。
境界によって、直線、平面、空間はそれぞれ図形の内部と外部に分割されます。図形の内部の点と外部の点を線で結ぶと必ず境界と交わります。
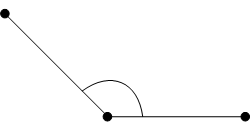
「角(カク,象形)」は∧型のつのを描いたもので、外側がかたく中空のつのを表しています。幾何においては二つの線が交わったときの∧型の部分を意味します。原論ではまず、一般の線に対する角を定義します。
定義1.1.7.2 (I-8)
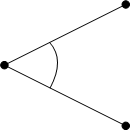
平面角へいめんかく, plane angleとは平面上で交わり、同一直線上にはない二つの線の間の傾きのことである。 これは交点における各々の接線が成す角のことを意味し、第Ⅲ巻において円と直線、円と円が接するということが定義され、円弧と弦の成す角等について論じられています。接線の成す角という意味を考えれば、平面角はすべて次の直線角であるとみなすことができます。
定義1.1.7.5 (I-9)
平面角を成す二つの線がともに直線であるとき、直線角ちょくせんかく, rectilinearという。 角という概念の本質は何でしょうか。ヒルベルトHilbert, David, 1862-1943はこれを交点から出る半直線の組とそれらに囲まれた領域のことであると定義しています。これは半直線の組から二つの角が導かれるため、その二つを区別するために角という領域には内部と外部があるということを明確に示したものです。そして、二つの半直線を辺へん, side、その交点を頂点ちょうてん, vertexと呼んでいます。いいかえれば、角はその二辺を境界とする図形です。角についてはこの定義がより具体的でわかりやすいと思われます。
二つの角を比較して等しい、大きい、小さいということは、頂点と一つの辺が一致するように作図する、すなわち図形としての角を運動させると領域として等しい、大きい、小さいということに一致します。二つの図形を重ね合わせて、領域の包含関係で比較するというのが、原論において量を測る基本的な技法であることが次節で述べられます。
原論では弧度法を使って角度を数で表現することはありませんが、直角を基準とし、その等分・等倍、鈍角、鋭角というような大掴みな分類で角度を論じています。
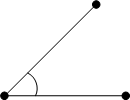
定義1.1.7.10 (I-10)
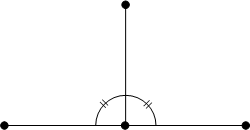
直線が別の直線の上に立ち、隣り合う角が互いに等しいときそれぞれの角を直角ちょっかく, right angleといい、その直線は別の直線と垂直すいちょく, perpendicularであるという。 直角と比較して大きいか小さいかで鈍角と鋭角を定義します。
「鈍(ドン,会意・形声)」は、音符の「屯(トン)」が草の芽が地上に出ようとしてなかなか出られないさまを表し、「金」と合わせて金属のかどがふくれてとがっていないことを意味します。
定義1.1.7.14 (I-11)
鈍角どんかく, obtuse angleとは直角より大きい角のことである。 「鋭(エイ,会意・形声)」は、音符の「兌(タイ=エイ)」がはぎとることを意味し、「金」と合わせてはぎとるために使うするどい金属のきっさきを意味します。
定義1.1.7.17 (I-12)
鋭角えいかく, acute angleとは直角より小さい角のことである。 第IV巻においては円に正多角形を内接あるいは外接させる作図法について論じられています。例えば命題IV-10「底辺を挟む角がそれぞれ残りの角の二倍であるような二等辺三角形を作図すること。」によって、命題IV-11「与えられた円に等辺で等角な五角形を内接させること。」を証明しています。
このように作図できる角については詳細に論じられていますが、原論はあくまでも数学の理論体系を構築することを目的としており、建築や工芸の現場においては、定規とコンパスの有限回の操作だけでは作図できない図形を描くことが必要になります。ドイツ・ルネサンスを代表する画家アルブレヒト・デューラーDürer, Albrecht, 1471-1528は『測定法教則』で「理論を学ばなければ真の工匠にはなりえない」と原論を賛美する一方で、さまざまな数学器具を使った実践的な近似作図法について詳細に解説しています。
「員(イン,会意)」は、三つの足(四足のものを方鼎という)と二つの耳をもつ器で、後に祭器となった「鼎(かなえ)」の象形である「貝」と丸いものの象形である「口」を会わせて、丸い形の器を意味し、転じてまるい物、物を数える単位を表わすようになりました。「圓(エン,会意・形声)」は「員」とまるい囲いの象形である「口」をさらに会わせて、まるい囲いを意味します。後に略されて「円」となりました。
定義1.1.8.2 (I-15/16)
円えん, circleとは円周えんしゅう, circumferenceと呼ばれる一つの線の境界で囲まれた平面図形であって、その中にある一つの点から円周上の点に引かれた直線の長さがすべて等しいようなものである。そして、その点を円の中心ちゅうしん, centerという。 「径(ケイ,会意・形声)」はまっすぐを意味する音符「坙(ケイ)」に、道を表す象形「彳」を合わせて、まっすぐで短い小道を表します。
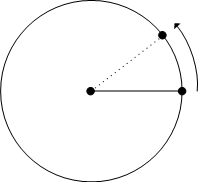
円の中心から円周上の点に引かれた線分もしくは線分の長さを半径はんけい, radiusといいます。円は中心を固定して半径を回転させたときの運動する端点の軌跡であると考えることができます。次節の公準3で円が自由に描けることが要請されます。
原論における次の定義は直径を定義しながら、それが円を二分することも要請しています。これはすべての平角が等しいことに対応しています。
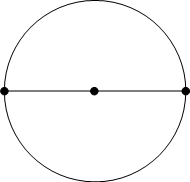
定義1.1.8.7 (I-17)
直径ちょっけい, diameterとは、円の中心を通り、円周上に両端をもつ直線であり、それによって円は二分される。人 物
ヒルベルト Hilbert, David, 1862-1943代表的著作『幾何学基礎論』において『原論』の平面幾何を公理論的に再構築しようと試みた。
アルブレヒト・デューラー Dürer, Albrecht, 1471-1528数 学
点 てん, point始点 してん, starting point
終点 しゅうてん, end point
端点 たんてん, edge point
線 せん, line
端 はし, edge
領域 りょういき, domain
連結 れんけつ, connected
直線 ちょくせん, straight line
線分 せんぶん, segment
無限直線 むげんちょくせん, infinite line
面 めん, surface
平面 へいめん, plain surface
境界 きょうかい, boundary
図形 ずけい, figure
平面角 へいめんかく, plane angle
直線角 ちょくせんかく, rectilinear
辺 へん, side
頂点 ちょうてん, vertex
直角 ちょっかく, right angle
垂直 すいちょく, perpendicular
鈍角 どんかく, obtuse angle
鋭角 えいかく, acute angle
円 えん, circle
円周 えんしゅう, circumference
中心 ちゅうしん, center
半径 はんけい, radius
直径 ちょっけい, diameter
Published by SANENSYA Co.,Ltd.