1.2 有向量
著者:梅谷 武
語句:並進,ベクトル,アフィン平面,並進群,推移的,等質空間,アフィン空間,アフィン標構,アフィン座標,正規直交基底,余弦定理,内積,クロネッカーのデルタ,外積,ベクトル積,法線ベクトル
有向量に関する用語と記号を整理する。
作成:2010-05-10
更新:2011-03-08
ベクトルとは平面あるいは空間上の並進を定めるものと考えてよい。
始点と終点が一致するものも有向線分と考え、これにより生成されるベクトルを0すると、ベクトル全体の集合であるベクトル空間は実数ℝ上の線形空間となる。
P ∈ E, a ∈ V2が与えられたとき、始点を
Pとする有向線分
PQ ∈ aを選び、
E × V2  E, (P,a) E, (P,a)  Q := P + a Q := P + a
|
と定めることによりベクトル空間
V2は加法群として平面
Eに右から作用する。この加法群を
並進群へいしんぐん, translation groupと呼ぶ。
V2の加法は
| | |
| | | P + (a + b),
P ∈ E, a, b ∈ V2 |
|
が成り立つように定義されている。
アフィン平面(E,V2)において、平面Eは並進群V2の等質空間である。
P ∈ U, a ∈ V3が与えられたとき、始点を
Pとする有向線分
PQ ∈ aを選び、
U × V3  U, (P,a) U, (P,a)  Q := P + a Q := P + a
|
と定めることによりベクトル空間
V3は並進群として空間
Uに右から作用する。
アフィン空間(U,V3)において、空間Uは並進群V3の等質空間である。
アフィン平面
(E,V2)に付随するベクトル空間
V2は二次元実線形空間であり、基底となるベクトルの組
(e1,e2)により、次のように表すことができる。
V2の任意の元
aは基底
(e1,e2)により一意的に
| a = λ1 e1 + λ2 e2,
λ1, λ2 ∈ ℝ
|
と表され、写像
V2  ℝ2,
a ℝ2,
a  (λ1, λ2) (λ1, λ2)
|
は実線形空間としての同型を与える。
アフィン空間
(U,V3)に付随するベクトル空間
V3は三次元実線形空間であり、基底となるベクトルの組
(e1,e2,e3)により、
と表すことができる。
V3の任意の元
aは基底
(e1,e2,e3)により一意的に
| a = λ1 e1 + λ2 e2 + λ3 e3,
λ1, λ2,λ3 ∈ ℝ
|
と表され、写像
V3  ℝ3,
a ℝ3,
a  (λ1, λ2, λ3) (λ1, λ2, λ3)
|
は実線形空間としての同型を与える。
さらに、
Uの原点
Oを与えることにより、アフィン標構
(O;e1,e2,e3)が定まる。空間
U上の任意の点
Pに対して
なる
aが一意的に定まるので、基底
(e1,e2,e3)を使って
| P = O + λ1 e1 + λ2 e2 + λ3 e3,
λ1, λ2,λ3 ∈ ℝ
|
と表現することができる。これにより定まる写像
U  ℝ3,
P ℝ3,
P  (λ1, λ2, λ3) (λ1, λ2, λ3)
|
は全単射であり、
(λ1, λ2, λ3)を点
Pのアフィン座標と呼ぶ。
平面ベクトルのノルムはベクトルの長さとして自然に定義することができる。ベクトル
a ∈ V2は平面上に二点
P,Qをとり、有向線分の同値類
a=[PQ]と表わすことができる。このとき、線長量
Lの単位
u ∈ L+が定められているならば
| :V2  ℝ,
a ℝ,
a  | | := | |
|
によって、ノルムを定める。
V2はこれによりノルム空間となる。
正規直交基底
(e1,e2)を定め、ベクトル
aを
と表現する。ベクトル
aの長さを
λ uとおくと、ピュタゴラスの定理から
| λ u ⊗ λ u =
| | u ⊗ | | u +
| | u ⊗ | | u
|
が成り立ち、テンソル積の双線形性により、
となり、
と求めることができる。
平面上の二点
P,Qの距離をノルムを使って次のように定義することができる。
これにより平面は距離空間となる。
正規直交基底
によって、二つのベクトル
a,bが次のように座標表現されているとする。
| | | λ1 e1 + μ1 e2 =
| 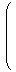 | | 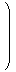 |
|
| | | λ2 e1 + μ2 e2 =
| 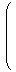 | | 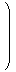 |
|
このとき余弦定理は次のように表現される。
| | |
| | | (λ12 + μ12) + (λ22 + μ22) -
2 cos θ √λ12 + μ12 √λ22 + μ22 |
|
に関して整理すると次の公式が導かれる。
平面に付随するベクトル空間
V2上の
内積ないせき, inner productを次のように定義する。
V2 × V2  A,
(a, b) A,
(a, b)  〈 a, b 〉 :=
cos θ 〈 a, b 〉 :=
cos θ | | ⊗ | |
|
正規直交基底を使って表現し、単位
uによる測定写像
(u ⊗ u)-1を合成すれば、次のような実双線形形式となる。
V2 × V2  ℝ,
(a, b) ℝ,
(a, b)  (u ⊗ u)-1(〈 a, b 〉) =
λ1 λ2 + μ1 μ2
(u ⊗ u)-1(〈 a, b 〉) =
λ1 λ2 + μ1 μ2
|
慣例により測定写像
(u ⊗ u)-1は書かない。
| 〈a, b〉
=
ta b
=
( λ1 μ1 )
| 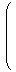 | | 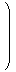 |
=
λ1 λ2 + μ1 μ2
|
平面に付随するベクトル空間
V2上の内積は双線形かつ対称、正値である。すなわち、次が成り立つ。
| (IN1)
| 〈 a + b, c 〉 = 〈 a, c 〉 + 〈 b, c 〉,
a,b,c ∈ V2
|
| (IN2)
| 〈 a, b + c 〉 = 〈 a, b 〉 + 〈 a, c 〉,
a,b,c ∈ V2
|
| (IN3)
| λ 〈 a, b 〉 = 〈 λ a, b 〉 = 〈 a, λ b 〉,
a,b ∈ V2, λ ∈ ℝ
|
| (IN4)
| 〈 a, b 〉 = 〈 b, a 〉,
a,b ∈ V2
|
| (IN5)
| 〈 a, a 〉 ≧ 0, a ∈ V2
かつ
〈 a, a 〉 = 0 ⇔
a = 0
|
平面上の任意のベクトル
a,bについて、次が成り立つ。
| (1.2) | | 〈 a, b 〉 = | |
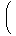 | | ⊗ | | -
| | ⊗ | |
- | | ⊗ | | 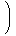
|
|
平面上の任意のベクトル
a,bについて、次が成り立つ。
平面に付随するベクトル空間
V2上の正規直交座標系
(O;e1,e2)について、次が成り立つ。
| (1.4) | | 〈 ei, ej 〉 = δij, i,j = 1,2
|
|
直線図形をその境界の頂点列ABCで表すときに直線図形の内部が有向線分AB, BC, CAの左側にあるとき、または回転が反時計回りであるとき、直線図形ABCは正の向きであるといい、右側にあるとき、回転が時計回りであるとき、負の向きであるという。正の向きの場合は表面、負の向きの場合は裏面を見ていると考える。
向き付けられた平面図形の面積は正の向きの場合は正の面積量、負の向きの場合は負の面積量であると定める。
平面に付随するベクトル空間
V2上の
外積がいせき, exterior productを次のように定義する。
V2 × V2  A,
(a, b) A,
(a, b)  a ∧ b :=
sin θ a ∧ b :=
sin θ | | ⊗ | |
|
これは二つの平面ベクトル
a,bが張る平行四辺形の面積に他ならない。
二つのベクトルが同じ場合は
と定義する。このことから
| (a+b) ∧ (a+b) = a ∧ b + b ∧ a = 0
|
となり、
が導かれる。
正規直交基底により、二つのベクトル
a,bが次のように座標表現されているとする。
| | | λ1 e1 + μ1 e2 =
| 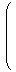 | | 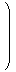 |
|
| | | λ2 e1 + μ2 e2 =
| 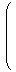 | | 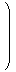 |
|
このとき、
| | | ( λ1 e1 + μ1 e2 ) ∧ ( λ2 e1 + μ2 e2 ) |
|
| | | λ1 e1 ∧ ( λ2 e1 + μ2 e2 )
+ μ1 e2 ∧ ( λ2 e1 + μ2 e2 ) |
|
| | | λ1 μ2 e1 ∧ e2
+ μ1 λ2 e2 ∧ e1 |
|
| | |
より、外積は次のように表現される。
V2 × V2  ℝ,
(a,b) ℝ,
(a,b)  a ∧ b =
det(a,b) := λ1 μ2 - μ1 λ2 a ∧ b =
det(a,b) := λ1 μ2 - μ1 λ2
|
平面に付随するベクトル空間
V2上の外積は双線形かつ交代である。すなわち、次が成り立つ。
| (EXT1)
| ( a + b ) ∧ c = a ∧ c + b ∧ c,
a,b,c ∈ V2
|
| (EXT2)
| a ∧ ( b + c ) = a ∧ b + a ∧ c,
a,b,c ∈ V2
|
| (EXT3)
| λ a ∧ b = λ a ∧ b = a ∧ λ b,
a,b ∈ V2, λ ∈ ℝ
|
| (EXT4)
| a ∧ a = 0, a ∈ V2
|
| (EXT5)
| a ∧ b = - b ∧ a, a,b ∈ V2
|
空間内の平面上にアフィン標構(O;e1,e2)を定め、それに垂直な基底ベクトルe3を決めるときに、その決め方は二通りある。それは平面によって空間が二つの領域に分割されるからである。そのどちらに原点を始点とする有向線分が属するかということを二つのベクトルの外積を利用して表現する。
外積e1 ∧ e2が定める平行四辺形が表になる方向を正の方向、裏になる方向を負の方向と定める。そして、e3が外積e1 ∧ e2の正の方向にあるとき、アフィン標構(O;e1,e2,e3)あるいは基底(e1,e2,e3)は右手系であるといい、負の方向にあるとき左手系であるという。
空間ベクトルのノルムもベクトルの長さとして定義することができる。ベクトル
a ∈ V3は空間内に二点
P,Qをとり、有向線分の同値類
a=[PQ]と表わすことができる。このとき、線長量
Lの単位
u ∈ L+が定められているならば
| :V3  ℝ,
a ℝ,
a  | | := | |
|
によって、ノルムを定める。
V3はこれによりノルム空間となる。
正規直交基底
(e1,e2,e3)を定め、ベクトル
aを
と表現する。ベクトル
aの長さを
λ uとおくと、ピュタゴラスの定理から
| λ u ⊗ λ u =
| | u ⊗ | | u +
| | u ⊗ | | u +
| | u ⊗ | | u
|
が成り立ち、テンソル積の双線形性により、
となり、
と求めることができる。
空間内の二点
P,Qの距離をノルムを使って次のように定義することができる。
これにより空間は距離空間となる。
空間内の二つのベクトル
a,bの内積は、それらが同一平面上にあることから平面ベクトルの内積と同様に定義することができる。
V3 × V3  A,
(a,b) A,
(a,b)  〈a,b〉 :=
cos θ 〈a,b〉 :=
cos θ | | ⊗ | |
|
正規直交基底
(e1,e2,e3)を定めたときの内積の座標表現を求める。二つのベクトル
a,bが次のように座標表現されているとする。
| | | λ1 e1 + μ1 e2 + ξ1 e3
=
| 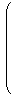 | | 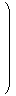 |
|
|
| | | λ2 e1 + μ2 e2 + ξ2 e3
=
| 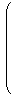 | | 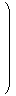 |
|
このとき余弦定理から次の公式が導かれる。
| cos θ = | | √λ12 + μ12 + ξ12√λ22 + μ22 + ξ22 |
|
|
|
線長量の単位
uにより
| | | √λ12 + μ12 + ξ12 u ⊗ √λ22 + μ22 + ξ22 u |
|
| | | √λ12 + μ12 + ξ12
√λ22 + μ22 + ξ22 u ⊗ u |
|
と書くことができるから、測定写像
(u ⊗ u)-1を合成すると次のようになる。
V3 × V3  ℝ,
(a,b) ℝ,
(a,b)  (u ⊗ u)-1(〈a,b〉)
= λ1 λ2 + μ1 μ2 + ξ1ξ2 (u ⊗ u)-1(〈a,b〉)
= λ1 λ2 + μ1 μ2 + ξ1ξ2
|
慣例により測定写像
(u ⊗ u)-1は書かない。
| 〈a,b〉
=
ta b
=
( λ1 μ1 ξ1 )
| 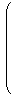 | | 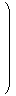 |
=
λ1 λ2 + μ1 μ2 + ξ1ξ2
|
空間に付随するベクトル空間
V3上の内積は双線形かつ対称、正値である。すなわち、次が成り立つ。
| (IN1)
| 〈 a + b, c 〉 = 〈 a, c 〉 + 〈 b, c 〉,
a,b,c ∈ V3
|
| (IN2)
| 〈 a, b + c 〉 = 〈 a, b 〉 + 〈 a, c 〉,
a,b,c ∈ V3
|
| (IN3)
| λ 〈 a, b 〉 = 〈 λ a, b 〉 = 〈 a, λ b 〉,
a,b ∈ V3, λ ∈ ℝ
|
| (IN4)
| 〈 a, b 〉 = 〈 b, a 〉,
a,b ∈ V3
|
| (IN5)
| 〈 a, a 〉 ≧ 0, a ∈ V3
かつ
〈 a, a 〉 = 0 ⇔ a = 0
|
空間内の任意のベクトル
a,bについて、次が成り立つ。
| (1.6) | | 〈 a, b 〉 = | |
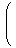
| | ⊗ | | -
| | ⊗ | | -
| | ⊗ | |
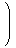
|
|
空間内の任意のベクトル
a,bについて、次が成り立つ。
空間に付随するベクトル空間
V3上の正規直交基底
(e1,e2,e3)について、次が成り立つ。
| (1.8) | | 〈 ei, ej 〉 = δij, i,j = 1,2,3
|
|
空間内の二つのベクトル
a,bの外積
a ∧ bは平面ベクトルの外積を利用して定義する。正規直交基底
(e1,e2,e3)により、二つのベクトル
a,bが次のように座標表現されているとする。
| a =
λ1 e1 + μ1 e2 + ξ1 e3
=
| 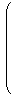 | | 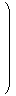 |
|
| b =
λ2 e1 + μ2 e2 + ξ2 e3
=
| 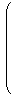 | | 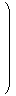 |
|
三つの基底ベクトルの二つから生成される座標平面を考える。
二つのベクトル
a,bのこれらの座標平面への射影を次のように記す。
| a23 = μ1 e2 + ξ1 e3,
b23 = μ2 e2 + ξ2 e3
|
| a31 = ξ1 e3 + λ1 e1,
b31 = ξ2 e3 + λ2 e1
|
| a12 = λ1 e1 + μ1 e2,
b12 = λ2 e1 + μ2 e2
|
各座標平面への射影の外積を計算する。
| | |
| | | ( μ1 ξ2 - ξ1 μ2 ) e2 ∧ e3
∈ A23 := ℝ e2 ∧ e3 |
|
| | |
| | | ( ξ1 λ2 - λ1 ξ2 ) e3 ∧ e1
∈ A31 := ℝ e3 ∧ e1 |
|
| | |
| | | ( λ1 μ2 - μ1 λ2 ) e1 ∧ e2
∈ A12 := ℝ e1 ∧ e2 |
|
これらの面積量はそれぞれ意味が異なるので別の種類の量と考える。そして空間ベクトルの外積を次のように定義する。
V3 × V3  A23 ⊕ A31 ⊕ A12,
(a,b)
A23 ⊕ A31 ⊕ A12,
(a,b)  a ∧ b a ∧ b
|
| a ∧ b :=
a23 ∧ b23 +
a31 ∧ b31 +
a12 ∧ b12
|
座標展開すると次のようになる。
| | | ( μ1 ξ2 - ξ1 μ2 ) e2 ∧ e3
+ ( ξ1 λ2 - λ1 ξ2 ) e3 ∧ e1
+ ( λ1 μ2 - μ1 λ2 ) e1 ∧ e2 |
|
| | |
e2 ∧ e3
-
| |
e3 ∧ e1
+
| |
e1 ∧ e2 |
|
空間に付随するベクトル空間
V3上の二つのベクトルの外積は双線形かつ交代である。すなわち、次が成り立つ。
| (EXT1)
| ( a + b ) ∧ c = a ∧ c + b ∧ c,
a,b,c ∈ V3
|
| (EXT2)
| a ∧ ( b + c ) = a ∧ b + a ∧ c,
a,b,c ∈ V3
|
| (EXT3)
| λ a ∧ b = λ a ∧ b = a ∧ λ b,
a,b ∈ V3, λ ∈ ℝ
|
| (EXT4)
| a ∧ a = 0, a ∈ V3
|
| (EXT5)
| a ∧ b = - b ∧ a, a,b ∈ V3
|
空間内の二つのベクトル
aと
bが張る平行四辺形の面積量は
aから
bへ反時計回りに向かう角度を
θとすると次のように表すことができる。
これを座標表現で計算する。
| | | √λ12 + μ12 + ξ12√λ22 + μ22 + ξ22 |
|
|
|
| | |
| | 
| | (λ12 + μ12 + ξ12)(λ22 + μ22 + ξ22)
- (λ1λ2 + μ1μ2 + ξ1ξ2)2 |
| (λ12 + μ12 + ξ12)(λ22 + μ22 + ξ22) |
|
|
 | |
|
より、線長量の単位を
u = e1 = e2 = e3とすると
| | |
| | | √(λ12 + μ12 + ξ12)(λ22 + μ22 + ξ22)
- (λ1λ2 + μ1μ2 + ξ1ξ2)2 u ⊗ u |
|
| | | √( μ1 ξ2 - ξ1 μ2 )2
+ ( ξ1 λ2 - λ1 ξ2 )2
+ ( λ1 μ2 - μ1 λ2 )2
u ⊗ u |
|
となることから、三種類の有向面積量の直和
A23 ⊕ A31 ⊕ A12上のノルムを
| :
A23 ⊕ A31 ⊕ A12  A+ A+
|
| λ e2 ∧ e3 + μ e3 ∧ e1 +
ξ e1 ∧ e2 |
|
:= √λ2 + μ2 + ξ2 u ⊗ u
|
と定めると、
a ∧ bは二つのベクトル
a,bを含む平面上で
aと
bが張る平行四辺形の面積量に一致する。
空間内の二つのベクトル
a,bの外積
a ∧ bのノルム
a ∧ bは
aと
bが張る平行四辺形の面積量である。
空間ベクトルの二項外積は座標系に依存するが、そのノルムは座標系に依存しない。
空間内の二つのベクトル
a,bのベクトル積
a × bは、これらのベクトルが張る向き付けられた平行四辺形に直交し、正方向にある。さらに、その単位線長比は平行四辺形の単位面積比に一致する。
ベクトル積a × bは、向き付けられた平行四辺形の法線方向と面積とを同時に表現する空間的量になっている。
空間に付随するベクトル空間
V3上のベクトル積について次が成り立つ。
| (VEC1)
| ( a + b ) × c = a × c + b × c,
a,b,c ∈ V3
|
| (VEC2)
| a × ( b + c ) = a × b + a × c,
a,b,c ∈ V3
|
| (VEC3)
| λ a × b = λ a × b = a × λ b,
a,b ∈ V3, λ ∈ ℝ
|
| (VEC4)
| a × a = 0, a ∈ V3
|
| (VEC5)
| a × b = - b × a, a,b ∈ V3
|
ベクトル積は結合的ではないが、次の性質によりベクトル空間V3はLie環になる。
空間に付随するベクトル空間
V3上のベクトル積について次が成り立つ。
| (1.9) | | a × (b × c)
= 〈a,c〉b - 〈a,b〉c,
a,b,c ∈ V3
|
|
空間に付随するベクトル空間
V3上のベクトル積について次が成り立つ。
| (1.10) | | a × (b × c)
+ b × (c × a)
+ c × (a × b) = 0
, a,b,c ∈ V3
|
|
空間内の三つのベクトル
a,b,cの外積
a ∧ b ∧ cはそれらが張る平行六面体の有向体積量として定義される。次の同値な三条件が満たされるときに正方向とし、そうでないときに負方向と定める。
| (1)
| b ∧ cの正方向にaがある。
|
| (2)
| c ∧ aの正方向にbがある。
|
| (3)
| a ∧ bの正方向にcがある。
|
この定義により次の性質が成り立つ。
空間に付随するベクトル空間
V3上の三つのベクトルの外積
V3 × V3 × V3  D,
(a,b,c) D,
(a,b,c)  a ∧ b ∧ c a ∧ b ∧ c
|
は多重線形かつ交代であり、右手系の正規直交基底
(e1,e2,e3)を定めるとき、その単位を
uとすれば次が成り立つ。
三つのベクトル
a,b,cが次のように座標表現されているとする。
| a =
λ1 e1 + μ1 e2 + ξ1 e3
=
|  | |  |
|
| b =
λ2 e1 + μ2 e2 + ξ2 e3
=
| 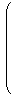 | | 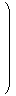 |
|
| c = λ3 e1 + μ3 e2 + ξ3 e3
=
| 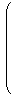 | | 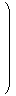 |
|
多重線形と交代性より
| a ∧ b ∧ c
=
det (a, b, c)
e1 ∧ e2 ∧ e3
|
となり、単位
uを使えば、
| a ∧ b ∧ c =
det (a, b, c) u ⊗ u ⊗ u
|
と書くことができる。これに測定写像
(u ⊗ u ⊗ u)-1を合成することにより、関数
detV3 × V3 × V3  ℝ,
(a,b,c) ℝ,
(a,b,c)  det (a,b,c) det (a,b,c)
|
が定まる。これは向きを変えない正規直交標構の座標変換に関して不変である。
二項外積とベクトルとの外積を多重線形かつ交代となるように自然に拡張すると、例えば次のような計算ができる。
| | |
| | 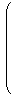 λ3
λ3
| |
-
μ3
| |
+
ξ3
| |
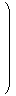 e1 ∧ e2 ∧ e3
e1 ∧ e2 ∧ e3
|
|
| | |
関数
detは
(3,3)行列に対する行列式を定める。
行列式は乗法群としての準同型写像になっている。
[
1] 梅谷 武,
幾何学事始, pisan-dub.jp, 2009
数 学
並進 へいしん, translation
ベクトル べくとる, vector
アフィン平面 あふぃんへいめん, affine plane
並進群 へいしんぐん, translation group
推移的 すいいてき, transitive
等質空間 とうしつくうかん, homogeneous space
アフィン空間 あふぃんくうかん, affine space
アフィン標構 あふぃんひょうこう, affine frame
アフィン座標 あふぃんざひょう, affine coordinates
正規直交基底 せいきちょっこうきてい,orthonormal basis
余弦定理 よげんていり, cosine theorem
内積 ないせき, inner product
クロネッカーのデルタ くろねっかーのでるた, Kronecker delta
外積 がいせき, exterior product
ベクトル積 べくとるせき, vector product
法線ベクトル ほうせんべくとる, normal vector