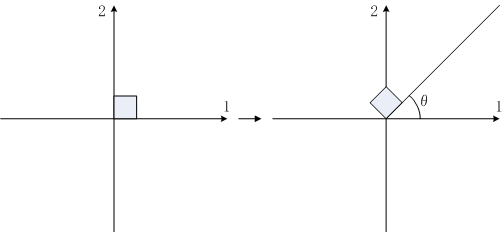
前節において合同変換群の原点の固定部分群は直交群O(V²)に一致することがわかりました。ここでは直交群の構造を2次行列表現O(2)で考えます。 より、 これを成分の関係式にすると 最初の二式から、α, β ∈ [0,4∠R)が一意的に存在して、 となり、最後の式より、 ですから、 となり、βをθと書き直せば が成り立ちます。最初の解は行列式が1であり、図形を反時計回りにθだけ回転させる回転行列かいてんぎょうれつ, rotation matrixです。

 回転行列の全体は直交群の部分群であり、回転群かいてんぐん, rotation groupSO(2)と呼ばれます。 二番目の解は、 と2軸に関して左右対称に裏返す鏡映きょうえい, reflectionと回転に分解することができます。

 この鏡映が生成する位数2の部分群をRef(2)と書くことにしましょう。直交群は鏡映群と回転群の直積に分解することができます。

 行列を位相群として考えるために、実数上の(n,n)行列全体をM(n,ℝ)に 次のようにノルムを導入します。

 このノルムにより、M(n,ℝ)上に距離を定義することができます。

 位相空間という概念を定義していませんが、ここでは距離が定義されていることと考えてかまいません。

 次に位相空間の連結性を定義しますが、ここでは弧状連結性として定義します。多様体上では連結性と弧状連結性が一致することがわかっており、ここで論じている線形Lie群も多様体です。

 平面上において、一点だけからなる集合は弧状連結ですが、二点以上の有限集合は弧状連結ではありません。一般線形群の中で鏡映群Ref(2)は弧状連結ではありません。連続写像 は全単射になるので、SO(2)は弧状連結です。

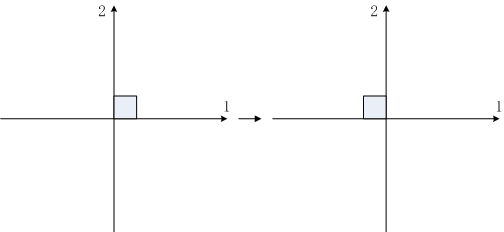
 ユークリッド幾何における運動とは、平面上の図形を合同変換によって連続的に動かすことをいいます。言い換えれば、運動とは合同変換群の単位元からの道のことです。したがって、平面における運動全体の集合、すなわち平面の運動群うんどうぐん, motion groupは合同変換群の単位元を含む弧状連結成分に他なりません。

 平面に付随するベクトル空間の回転群を次のようにおきます。 運動群の原点の固定部分群は回転群SO(V²)に一致します。