6. 最短経路問題
著者:梅谷 武
重み付きグラフの最短経路問題をダイクストラのアルゴリズムで解く。
作成:2023-10-14
更新:2024-10-23
更新:2024-10-23
ここではグラフとして連結単純グラフを考えることにする。
重み付きグラフG = (V,E,φ,w)の部分グラフHの重さw(H)は
により定義される。多くの最適化問題はある性質をもつ最軽量の部分グラフを求めることに帰着される。二頂点間の最軽量の経路、言い換えれば最短経路を求める問題が最短経路問題さいたんけいろもんだい, shortest path problem(shortest path problem)である。
| w(H) = |
|
重み付きグラフGの二頂点u,vを結ぶ道の重さを長さ(length)、二頂点u,vを結ぶ最短経路の長さを二頂点間の距離(distance)と呼び、d(u,v)と書くことにする。また頂点uと部分グラフHについて
と定義する。
| d(u,H) := |
|
u0∈S⊊V(G)、Sc := V(G)-Sとするとき、d(u0,Sc)を与えるv∈Scが存在し、u0とvを結ぶ最短路が
となる。このとき
であり、
が成り立つ。
| u0, u1, ⋯ un-1, un = v, u0,⋯,un-1∈S, un=v∈Sc |
| d(u0,v) = d(u0,un-1) + w(un-1v) |
| d(u0,Sc) = |
|
S0 := {u0}とし、それに頂点を追加しながら
というu0からすべての頂点への最短経路が求まった頂点集合SiのGまで到達する拡大列を作るのがダイクストラ(Dijkstra)のアルゴリズムである。
| S0 ⊂ S1 ⊂ ⋯ ⊂ Si ⊂ ⋯ ⊂ G |
|
|
| ||||||
|
|
ダイクストラのアルゴリズムは最短経路が複数ある場合にそのうちの一つを求めて終わる。すべての最短経路を求めるにはアルゴリズムの変更が必要になる。詳細についてはⅣ-1の参考文献を参照のこと。
- ハッシュ表dを初期化、d(v0) := 0, d(v) := ∞(v≠v0)
- ハッシュ表parentを初期化
- 優先度付きキューpqを初期化、pqに(0,v0)をpush
- while (pqは空でない)
- pqから(d,v)をpop
- for (vのすべての近傍nbr)
- alt := d(v) + w(u,nbr)
- if (alt < d(v))
- d(v) := alt
- Parent(nbr) := v
- pqに(alt,nbr)をpush
- dとParentを返す。
dijkstra.rkt
#lang racket
(require data/heap)
(require "graph.rkt")
(provide dijkstra graph-to-dot-dijkstra)
(define (dijkstra g start)
(define vertices (get-vertices g))
(define distance (make-hash))
(define parent (make-hash))
(for ([v vertices])
(hash-set! distance v +inf.0))
(hash-set! distance start 0)
(define pq (make-heap (λ (a b) (< (car a) (car b)))))
(heap-add! pq (cons 0 start))
(let loop ()
(unless (zero? (heap-count pq))
(define d (car (heap-min pq)))
(define v (cdr (heap-min pq)))
(heap-remove-min! pq)
(for ([nbr (neighbors g v)])
(define key (make-key v nbr (get-type g)))
(define edge (car (hash-ref (get-fibers g) key)))
(define w (weight g edge))
(define alt (+ d w))
(when (< alt (hash-ref distance nbr))
(hash-set! distance nbr alt)
(hash-set! parent nbr v)
(heap-add! pq (cons alt nbr))))
(loop)))
; rooted spanning tree
(define rst (make-graph 'directed))
(for-each (λ (v) (add-vertex! rst v)) vertices)
(for ([v (hash-keys parent)])
(define u (hash-ref parent v))
(define key (make-key u v (get-type g)))
(define edge (car (hash-ref (get-fibers g) key)))
(add-edge! rst u v edge))
; return values
(values distance parent rst))
(define (graph-to-dot-dijkstra g distance rst filename)
(call-with-output-file filename
(λ (out)
(define graph-label (if (eq? (get-type g) 'undirected) "graph" "digraph"))
(define edge-connector (if (eq? (get-type g) 'undirected) "--" "->"))
(fprintf out "~a G {\n" graph-label)
(for-each
(λ (v)
(define dist (hash-ref distance v))
(fprintf out " ~a [label=\"~a:~a\" shape=circle];\n" v v dist))
(get-vertices g))
(for-each
(λ (e)
(define edge (hash-ref (get-edges g) e))
(define v1 (car edge))
(define v2 (cdr edge))
(define label (if (weighted? g)
(number->string (weight g e))
(symbol->string e)))
(define is-in-rst (or (edge? rst v1 v2) (edge? rst v2 v1)))
(define style
(if is-in-rst
" [label=\"~a\" penwidth=2.5]"
" [label=\"~a\"]"))
(fprintf out " ~a ~a ~a~a;\n"
v1 edge-connector v2 (format style label)))
(hash-keys (get-edges g)))
(fprintf out "}\n"))
#:exists 'replace))
Ⅳ-1の参考文献[9]の例題2.12の例である。[9]にはアルゴリズムの流れがステップ毎の図で説明されている。
graph61.rkt:
#lang racket
(require "graph.rkt")
(require "dijkstra.rkt")
(define graph61 (make-graph 'undirected))
(add-vertex! graph61 'a)
(add-vertex! graph61 'b)
(add-vertex! graph61 'c)
(add-vertex! graph61 'd)
(add-vertex! graph61 's)
(add-vertex! graph61 't)
(add-weighted-edge! graph61 's 'a 'e1 1)
(add-weighted-edge! graph61 's 'c 'e2 3)
(add-weighted-edge! graph61 't 'b 'e3 2)
(add-weighted-edge! graph61 't 'd 'e4 5)
(add-weighted-edge! graph61 'a 'b 'e5 8)
(add-weighted-edge! graph61 'a 'c 'e6 4)
(add-weighted-edge! graph61 'b 'c 'e7 2)
(add-weighted-edge! graph61 'b 'd 'e8 4)
(add-weighted-edge! graph61 'c 'd 'e9 3)
(graph-to-dot graph61 "graph61.dot")
(define-values (dist par rst) (dijkstra graph61 's))
(displayln dist)
(displayln par)
(graph-to-dot-dijkstra graph61 dist rst "graph61-rst.dot")
次のgraph61.dotとgraph61-rst.dotは上記プログラムの出力をエディタで編集したものである。
graph61.dot:
graph G {
layout=neato;
node [shape=circle];
s [pos="0,1!"];
t [pos="3,1!"];
a [pos="1,2!"];
b [pos="2,2!"];
c [pos="1,0!"];
d [pos="2,0!"];
s -- a [label="1"];
a -- c [label="4"];
b -- c [label="2"];
t -- b [label="2"];
c -- d [label="3"];
t -- d [label="5"];
a -- b [label="8"];
s -- c [label="3"];
b -- d [label="4"];
}
graph61.png:
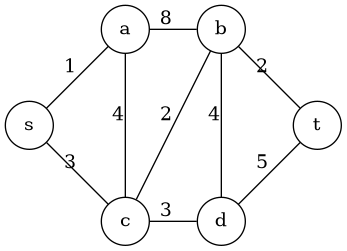

graph61-rst.dot:
graph G {
layout=neato;
node [shape=circle];
s [pos="0,1!"];
t [pos="3,1!"];
a [pos="1,2!"];
b [pos="2,2!"];
c [pos="1,0!"];
d [pos="2,0!"];
s -- a [label="1"];
a -- c [label="4"];
b -- c [label="2"];
t -- b [label="2"];
c -- d [label="3"];
t -- d [label="5"];
a -- b [label="8"];
s -- c [label="3"];
b -- d [label="4"];
}
graph61-rst.png:
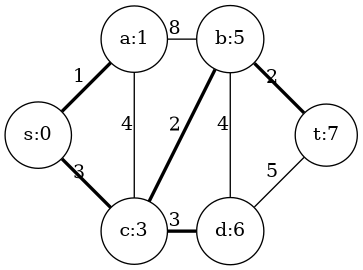

This document is licensed under the MIT License.
Copyright (C) 2024 Takeshi Umetani