3. 木と最小全域木
著者:梅谷 武
木に関する用語を定義し、最小全域木の求め方について述べる。
作成:2023-04-07
更新:2024-10-23
更新:2024-10-23
定義3.1 木
グラフが閉路をもつことを巡回じゅんかい, cyclic(cyclic)、閉路をもたないことを非巡回ひじゅんかい, acyclic(acyclic)という。木き, tree(tree)とは連結な非巡回グラフのことである。森もり, forest(forest)とは非連結な非巡回グラフのことである。単一の頂点のみから成る木を自明な木じめいなき, trivial tree(trivial tree)という。木や森において次数1の頂点を葉は, leaf(leaf)という。
命題3.2 木の性質
- 木の任意の二頂点間にはただ一つの道が存在する。
- 頂点数が2以上の木には葉が少なくとも1個存在する。
- 木の頂点の個数は辺の個数より一つ多い。
- 頂点数が2以上の木には葉が少なくとも2個存在する。
証明
(1):連結性から木の二頂点v,wを結ぶ歩道そして道が存在する。このような道が二つあるとすればそれらをつないで閉じた歩道を作ることができて、それには回路そして閉路が含まれる。これは木であることに反するので、このような道は唯一つである。(2):任意の頂点vを選び、それに接続する辺eとeのvとは異なる端点v'を定める。仮定よりこのような辺eと端点v'は存在する。v'の次数が1であれば終わる。そうでなければv'に接続する辺e'を選べる。このようにしてvから始まる道を伸ばしていくと仮定より回路にはならないので頂点の有限性より必ず終点がある。この終点の次数は1である。
(3):頂点数に関する帰納法による。一つの頂点から成る自明な木は辺を含まない。二つの頂点から成る木は辺を一つ含む。頂点数kの木の辺数がk-1であることを帰納法の仮定とし、頂点数k+1の木Tの辺数がkであることを示す。
(2)よりTには次数1の頂点vがある。vは辺eで他の部分とつながっている。vとeを除いたグラフをT'とする。T'は回路を含まず、任意の二点を結ぶ歩道があるので木である。T'は頂点数kであり、帰納法の仮定より辺数はk-1である。TはT'に頂点vと辺eを加えたものなので、Tの辺数はkである。
(4):T = (V,E)とする。(2)より次数1の頂点は少なくとも1個ある。これ以外の頂点次数がすべて2以上とすると次数の和は
| 2(|V| - 1) + 1 |
| 2|E| = 2(|V| - 1) |
定理3.3 木の特徴付け
グラフG = (V,E)について次は同値である。- Gは木である。すなわち連結で閉路をもたない。
- Gの任意の二頂点間は唯一つの道で結ばれる。
- Gは連結で、|E| = |V|-1である。
- Gは閉路をもたず、|E| = |V|-1である。
証明
(1)⇒(2):命題3.2(1).(2)⇒(1):任意の二頂点間を結ぶ道があるので連結である。また命題3.2(2)の証明から任意の二頂点間を結ぶ道が唯一つであれば閉路を含まない。
(1)⇒(3):命題3.2(3).
(3)⇒(1):Gに閉路Cが含まれるとする。命題1.10(3)よりCから一辺を除いたグラフをG'とするとG'は連結である。G'が閉路をもつなら、同じ操作で閉路から一辺を除き連結部分グラフを得る。この操作を繰り返すと最終的には閉路をもたない連結部分グラフG''を得るがその作り方により|G| = |G''|で辺数は|E|より少ない。G''は木であるからこれは矛盾である。したがってGは閉路をもたない。
(1)⇒(4):命題3.2(3).
(4)⇒(1):Gが連結でないとするとGを連結成分に分けることができる。
| G = G1 ∪ G2 ∪ ⋯ ∪ Gn |
| |E| = |
| , |V| = |
|
定義3.4 根付き木
根付き木ねつきぎ, rooted tree(rooted tree)とは根ね, root(root)と呼ばれる一つの頂点が定められた木のことである。根付き木において任意の頂点を定めたとき、根とその頂点を結ぶ道が唯一つ存在する。その道の長さ(辺数)をその頂点のレベルれべる, level(level)という。根自身のレベルは0である。
根付き木におけるレベルの最大値を、その根付き木の高さたかさ, height(height)という。
根付き木において、ある頂点の子こ, child(child)とは、その頂点に隣接する頂点でその頂点よりもレベルが一つ高い頂点のことである。
根付き木において、ある頂点の親おや, parent(parent)とは、その頂点に隣接する頂点でその頂点よりもレベルが一つ低い頂点のことである。
根付き木において、同じ親の子であるような相異なる頂点を兄弟きょうだい, sibling(sibling)という。
根付き木において、根からある頂点wへの道の途中にある頂点vについて、vをwの先祖せんぞ, ancestor(ancestor)といい、wをvの子孫しそん, descendant(descendant)という。
根付き木において、子をもつ頂点を内点ないてん, internal vertex(internal vertex)という。根は葉になる可能性がある唯一の内点である。
定義3.5 部分木
根付き木Tにおいて、ある内点vの子孫全体の集合をV'、V'の各頂点に接続する辺全体の集合をE'とするとき、グラフT' = (V',E')はTの部分グラフである。これはvを根とする根付き木であり、vを根とする部分木ぶぶんぎ, subtree(subtree)と呼ばれる。 家系図のように兄弟に順序が付いているときは順序木を使って表現する。
定義3.6 順序木
兄弟に順序が付いている根付き木を順序木じゅんじょぎ, ordered tree(ordered tree)という。 実際の応用では順序木における兄弟数を制限することが多い。
定義3.7 m分木
兄弟数が高々m個であるような順序木をm分木mぶんぎ, m-ary tree(m-ary tree)という。特にm = 2のとき、二分木にぶんぎ, binary tree(binary tree)という。
二分木における兄弟の兄を左、弟を右で指し示す。内点の左の子を頂点とする部分木を左部分木ひだりぶぶんぎ, left subtree(left subtree)、右の子を頂点とする部分木を右部分木みぎぶぶんぎ, right subtree(right subtree)という。
定義3.9 重み付きグラフ
グラフG = (V,E,φ)が重み関数w:E → ℝ(非負値)をもつとき、G = (V,E,φ,w)を重み付きグラフおもみつきぐらふ, weighted graph(weighted graph)という。重み付きグラフG = (V,E,φ,w)の重さw(G)とはそのすべての辺の重みの総和のことである。| w(G) = |
|
定義3.10 最小全域木
重み付きグラフの最軽量全域木を最小全域木さいしょうぜんいきぎ, minimum spanning tree(minimum spanning tree)という。 最小全域木を求めるクラスカル(Kruskal)のアルゴリズム[2]を実装する。
素集合構造あるいはUnion-Find木[1]と呼ばれるデータ構造を準備しておく。
- make-disjoint-set:各頂点にその親となる頂点を対応させるハッシュ表parentを、各頂点に対して自分自身を親として初期化する。ハッシュ表rankは各頂点にその木の高さを対応させるもので、木を結合するときにその高さを低くするために使われる。
- find:指定した頂点の親を返す。
- union:二つの頂点が共通の親をもたなければそれらを結合する。
(define (make-disjoint-set vertices)
(define parent (make-hash))
(define rank (make-hash))
(for-each (λ (v)
(hash-set! parent v v)
(hash-set! rank v 0))
vertices)
(list parent rank))
(define (find parent x)
(if (equal? (hash-ref parent x) x)
x
(begin
(hash-set! parent x (find parent (hash-ref parent x)))
(hash-ref parent x))))
(define (union parent rank x y)
(define root-x (find parent x))
(define root-y (find parent y))
(unless (equal? root-x root-y)
(let ([rank-x (hash-ref rank root-x)]
[rank-y (hash-ref rank root-y)])
(cond [(< rank-x rank-y) (hash-set! parent root-x root-y)]
[(> rank-x rank-y) (hash-set! parent root-y root-x)]
[else
(hash-set! parent root-y root-x)
(hash-set! rank root-x (+ rank-x 1))]))))
G = (V(G),E(G),φ,w)の最小全域木Tを求める。
- V(T) := V(G), E(T) := ∅
- n := |V(T)|, w(e1)≦w(e2)≦⋯≦ w(en)となるよう添え字を付ける。
- 素集合構造を初期化。i := 1
- while (|E(T)| < n-1)
- eiの端点対(x,y)について共通の親をもたなければE(T)にeiを追加し、i := i + 1とし、xとyを結合する。
- T = (V(T),E(T))を返す。
(define (kruskal-mst g)
(define vertices (get-vertices g))
(define edges (sort (hash-keys (get-edges g))
(λ (e1 e2) (< (weight g e1) (weight g e2)))))
(define mst (make-graph (get-type g)))
(define disjoint-set (make-disjoint-set vertices))
(define parent (first disjoint-set))
(define rank (second disjoint-set))
(for-each (λ (v) (add-vertex! mst v)) vertices)
(define n (length vertices))
(define edge-count 0)
(for ([edge edges])
(when (< edge-count (- n 1))
(define v1 (car (hash-ref (get-edges g) edge)))
(define v2 (cdr (hash-ref (get-edges g) edge)))
(unless (equal? (find parent v1) (find parent v2))
(add-weighted-edge! mst v1 v2 edge (weight g edge))
(union parent rank v1 v2)
(set! edge-count (+ edge-count 1)))))
mst)
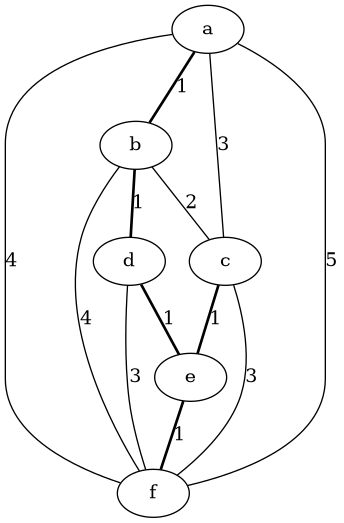
graph31.rkt:
#lang racket
(require "graph.rkt")
(require "kruskal.rkt")
(define graph31 (make-graph 'undirected))
(add-vertex! graph31 'a)
(add-vertex! graph31 'b)
(add-vertex! graph31 'c)
(add-vertex! graph31 'd)
(add-vertex! graph31 'e)
(add-vertex! graph31 'f)
(add-weighted-edge! graph31 'a 'b 'e1 1)
(add-weighted-edge! graph31 'a 'c 'e2 3)
(add-weighted-edge! graph31 'b 'c 'e3 2)
(add-weighted-edge! graph31 'b 'd 'e4 1)
(add-weighted-edge! graph31 'c 'e 'e5 1)
(add-weighted-edge! graph31 'd 'e 'e6 1)
(add-weighted-edge! graph31 'd 'f 'e7 3)
(add-weighted-edge! graph31 'e 'f 'e8 1)
(add-weighted-edge! graph31 'b 'f 'e9 4)
(add-weighted-edge! graph31 'c 'f 'e10 3)
(add-weighted-edge! graph31 'a 'f 'e11 5)
(add-weighted-edge! graph31 'a 'f 'e12 4)
(define mst (kruskal-mst graph31))
(gen-dot-png graph31 mst "graph31.dot")
graph31.png:

#lang racket
(require "graph.rkt")
(provide make-disjoint-set find union
has-cycle? kruskal-mst gen-dot-png)
(define (make-disjoint-set vertices)
(define parent (make-hash))
(define rank (make-hash))
(for-each (λ (v)
(hash-set! parent v v)
(hash-set! rank v 0))
vertices)
(list parent rank))
(define (find parent x)
(if (equal? (hash-ref parent x) x)
x
(begin
(hash-set! parent x (find parent (hash-ref parent x)))
(hash-ref parent x))))
(define (union parent rank x y)
(define root-x (find parent x))
(define root-y (find parent y))
(unless (equal? root-x root-y)
(let ([rank-x (hash-ref rank root-x)]
[rank-y (hash-ref rank root-y)])
(cond [(< rank-x rank-y) (hash-set! parent root-x root-y)]
[(> rank-x rank-y) (hash-set! parent root-y root-x)]
[else
(hash-set! parent root-y root-x)
(hash-set! rank root-x (+ rank-x 1))]))))
(define (has-cycle? g)
(define vertices (get-vertices g))
(define edges (hash-keys (get-edges g)))
(define disjoint-set (make-disjoint-set vertices))
(define parent (first disjoint-set))
(define rank (second disjoint-set))
(for/or ([edge edges])
(define v1 (car (hash-ref (get-edges g) edge)))
(define v2 (cdr (hash-ref (get-edges g) edge)))
(let ([root1 (find parent v1)]
[root2 (find parent v2)])
(if (equal? root1 root2)
#t
(begin
(union parent rank v1 v2)
#f)))))
(define (kruskal-mst g)
(define vertices (get-vertices g))
(define edges (sort (hash-keys (get-edges g))
(λ (e1 e2) (< (weight g e1) (weight g e2)))))
(define mst (make-graph (get-type g)))
(define disjoint-set (make-disjoint-set vertices))
(define parent (first disjoint-set))
(define rank (second disjoint-set))
(for-each (λ (v) (add-vertex! mst v)) vertices)
(define n (length vertices))
(define edge-count 0)
(for ([edge edges])
(when (< edge-count (- n 1))
(define v1 (car (hash-ref (get-edges g) edge)))
(define v2 (cdr (hash-ref (get-edges g) edge)))
(unless (equal? (find parent v1) (find parent v2))
(add-weighted-edge! mst v1 v2 edge (weight g edge))
(union parent rank v1 v2)
(set! edge-count (+ edge-count 1)))))
mst)
(define (gen-dot-png g mst filename)
(define type (if (eq? (get-type g) 'undirected) "graph" "digraph"))
(define arr (if (eq? (get-type g) 'undirected) "--" "->"))
(define mst-edges (get-edges mst))
(define dot-code
(string-append
(format "~a G {\n" type)
(for/fold ([code ""]) ([edge (hash-keys (get-edges g))])
(define v1 (car (hash-ref (get-edges g) edge)))
(define v2 (cdr (hash-ref (get-edges g) edge)))
(define weight 0)
(if (weighted? g)
(set! weight (hash-ref (get-weight g) edge))
(void))
(define is-mst-edge (hash-has-key? mst-edges edge))
(if (weighted? g)
(string-append code
(format " ~a ~a ~a [label=\"~a\"~a];\n"
v1 arr v2 weight
(if is-mst-edge ", style=bold, penwidth=2" "")))
(string-append code
(format " ~a ~a ~a [label=\"~a\"~a];\n"
v1 arr v2 (symbol->string edge)
(if is-mst-edge ", style=bold, penwidth=2" "")))))
"}\n"))
(call-with-output-file filename
(λ (out) (display dot-code out)) #:exists 'truncate)
(define name (first (string-split filename ".")))
(define pngname (string-append name ".png"))
(define cmd (string-append "dot -Tpng " filename " -o " pngname))
(displayln cmd)
(system cmd))
[1] Wikipedia, Disjoint-set data structure, Wikimedia Foundation, Inc., 2024
[2] Wikipedia, Kruskal's algorithm, Wikimedia Foundation, Inc., 2024
語 句
巡回 じゅんかい, cyclicグラフが閉路をもつこと。
非巡回 ひじゅんかい, acyclicグラフが閉路をもたないこと。
木 き, tree連結な非巡回グラフのこと。
森 もり, forest非連結な非巡回グラフのこと。
自明な木 じめいなき, trivial tree単一の頂点のみから成る木のこと。
葉 は, leaf木や森における次数1の頂点のこと。
根付き木 ねつきぎ, rooted tree根と呼ばれる一つの頂点が定められた木のこと。
根 ね, root木における一つの頂点で根付き木の構造を定めるもののこと。
レベル れべる, level根付き木における各頂点の根からの長さのこと。
高さ たかさ, height根付き木におけるレベルの最大値のこと。
子 こ, child根付き木において、ある頂点に隣接する頂点でその頂点よりもレベルが一つ高い頂点のこと。
親 おや, parent根付き木において、ある頂点に隣接する頂点でその頂点よりもレベルが一つ低い頂点のこと。
兄弟 きょうだい, sibling根付き木における同じ親の子であるような相異なる頂点のこと。
先祖 せんぞ, ancestor根付き木において、根からある頂点wへの道の途中にある頂点vについて、vをwの先祖という。
子孫 しそん, descendant根付き木において、根からある頂点wへの道の途中にある頂点vについて、wをvの子孫という。
内点 ないてん, internal vertex根付き木における子をもつ頂点のこと。
部分木 ぶぶんぎ, subtree根付き木におけるある内点vの子孫全体とそれに接続する辺全体から成る部分グラフのこと。これはvを根とする根付き木であり、部分木と呼ばれる。
順序木 じゅんじょぎ, ordered tree兄弟に順序が付いている根付き木のこと。
m分木 mぶんぎ, m-ary tree兄弟数が高々m個であるような順序木のこと。
二分木 にぶんぎ, binary tree兄弟数が高々2個であるような順序木のこと。
左部分木 ひだりぶぶんぎ, left subtree内点の左の子を頂点とする部分木のこと。
右部分木 みぎぶぶんぎ, right subtree内点の右の子を頂点とする部分木のこと。
全域木 ぜんいきぎ, spanning tree全域部分グラフが木であること。
重み付きグラフ おもみつきぐらふ, weighted graph重み関数(辺集合上の非負実数関数)をもつグラフのこと。
最小全域木 さいしょうぜんいきぎ, minimum spanning tree重み付きグラフにおける最軽量全域木のこと。
This document is licensed under the MIT License.
Copyright (C) 2024 Takeshi Umetani