2. 道と閉路

著者:梅谷武

道と閉路に関連する用語を定義し、オイラーグラフについて述べる。

作成:2023-04-07
更新:2024-10-25

2.1 道と閉路

本章ではグラフは無向グラフとして考える。有向グラフの場合はそれを無向グラフとみなすか、あるいは方向性を考慮した議論にする必要がある。

定義2.1 歩道,小道,道

グラフGの頂点v,wが与えられたとき、vからwへの歩道ほどう, walk(walk)とはv₀ = v, v_n = w (n＞0)なるn + 1個の隣接する頂点列

v₀, v₁, ⋯, v_n

とn個の隣接する辺の列

e₁, ⋯, e_n

から作られる隣り合った頂点と辺が接続しているような頂点と辺の交互列

v₀, e₁, v₁, e₂, ⋯, v_n-1, e_n, v_n

のことである。このときvを始点してん, start vertex(start vertex)、wを終点しゅうてん, end vertex(end vertex)という。
vからwへの小道こみち, trail(trail)とは辺が重複しない歩道のことである。小道を定める相異なる辺の列

e₁, ⋯, e_n

の辺数nを小道の長さという。
vからwへの道みち, path(path)とは頂点が重複しない小道のことである。
始点と終点が一致している歩道(小道,道)を閉じたとじた, closed(closed)歩道(小道,道)といい、一致しない歩道(小道,道)を開いたひらいた, open(open)歩道(小道,道)という。
閉じた小道を回路かいろ, circuit(circuit)、閉じた道を閉路へいろ, cycle(cycle)という。長さkの閉路をk-閉路k-へいろ, k-cycle(k-cycle)といい、kが奇数のとき奇閉路きへいろ, odd cycle(odd cycle)、偶数のとき偶閉路ぐうへいろ, even cycle(even cycle)という。

定義2.2 連結性

グラフGにおいて二つの頂点v,wが連結れんけつ, connected(connected)であるとは、vからwへの歩道が存在することである。
グラフGが連結れんけつ, connected(connected)であるとは、Gの任意の二頂点が連結であることをいう。

連結性はグラフの頂点集合上の同値関係であり、それにより頂点集合を分割することができる。その各分割を連結成分と呼ぶ。連結成分は次のように特徴付けることができる。ここではこれを連結成分の定義とする。

定義2.3 連結成分

グラフHがグラフGの連結成分れんけつせいぶん, connected component(connected component)であるとは、HはGの連結部分グラフであり、Hを真に含むGの部分グラフが連結にならないことである。

補題2.4

グラフGにおいて二頂点v,w間を結ぶ歩道にはv,w間を結ぶ小道が含まれ、v,w間を結ぶ小道にはv,w間を結ぶ道が含まれる。

証明

v,w間を結ぶ歩道を

v₀=v, e₁, v₁, e₂, ⋯, v_n-1, e_n, v_n=w.

に重複辺p,e,qがあったとすると重複の仕方は

⋯,p,e,q,⋯,q,e,p,⋯

と

⋯,p,e,q,⋯,p,e,q,⋯

の二種類である。前者の場合は回路p,e,q,⋯,q,e,pを除いて

⋯,p,⋯

とし、後者の場合は回路⋯,p,e,qを除いて

⋯,p,e,q,⋯

とすると重複辺p,e,qを作る回路が除かれる。これを繰り返せばすべての重複辺が除かれてv,w間を結ぶ小道ができる。
v,w間を結ぶ小道に重複点pがあったとすると重複の仕方は

⋯,p,⋯,p,⋯

となる。回路p,⋯,pを除いて

⋯,p,⋯

とすると重複点を作る回路が除かれる。これを繰り返せばすべての重複点が除かれてv,w間を結ぶ道ができる。■

命題2.5

連結グラフの任意の二頂点間を結ぶ道が存在する
回路に含まれる二頂点はその回路から一辺を除いても小道で結ばれる。
連結グラフの回路から一辺を除いても連結である。

証明

(1):補題2.4より。
(2):p,qを含む回路を

v,⋯,p,⋯,q,⋯,v

とすると左の⋯から一辺を除いたときは

p,⋯,q,⋯,v

中の⋯から一辺を除いたときは

q,⋯,v,⋯,p

右の⋯から一辺を除いたときは

v,⋯,p,⋯,q

がそれぞれp,qを通る小道となる。
(3):連結グラフGの回路Cから一辺eを除いたグラフG'が連結であることを示す。G'の任意の頂点v,wをとる。Gの連結性からv,wを結ぶ歩道Wが存在する。
case 1):eがWに含まれないときはWはG'の歩道である。
case 2):eがWに含まれるときは(2)の方法で作った小道を使ってeに置き換えた歩道をW'とするとW'はv,wを結ぶG'の歩道である。
いずれの場合もv,wを結ぶG'の歩道が存在し、G'は連結である。■

2.2 オイラーグラフ

定義2.6 オイラー回路

グラフGのオイラー小道おいらーこみち, Eulerian trail(Eulerian trail)とはGのすべての辺を含む小道のことであり、オイラー回路おいらーかいろ, Eulerian circuit(Eulerian circuit)とはGのすべての辺を含む回路のことである。

オイラー小道をもつグラフを準オイラーグラフじゅんおいらーぐらふ, semi-Eulerian graph(semi-Eulerian graph)、オイラー回路をもつグラフをオイラーグラフおいらーぐらふ, Eulerian graph(Eulerian graph)という。

補題2.7

グラフGの各頂点の次数が2以上であればGは閉路を含む。

証明

Gがループか多重辺を含めば閉路を含むのでGは単純グラフであるとする。vを任意の頂点とし、頂点列

v₀ = v, v₁, ⋯, v_i. ⋯

をv_i+1がv_iに隣接するように選んでいく。各頂点の次数は2以上なので重複する頂点に到達するまで伸ばしていくことができる。これは閉路となる。■

定理2.8 オイラーグラフ

連結グラフGがオイラー回路をもつための必要十分条件はすべての頂点の次数が偶数となることである。

証明

[⇒]:Gのオイラー回路Pのある頂点vを定めて始点とし、そこから回路を辿りながら、各頂点を通過するときに頂点毎の加算器に通過した辺数を加算していくと最終的に始点は終点と一致して終わる。このとき始点(終点)以外の頂点は通過するときに入力と出力を合わせて2だけ増えていき、始点も出力1が最終的には入力1が加わるので全頂点の次数は偶数になる。
[⇐]:Gの各頂点の次数が偶数であるとすると上の補題2.7から閉路Cを含む。CがGのすべての辺を含めばオイラー回路になる。CがGのすべての辺を含まないと仮定する。GからCを除いた部分グラフをHとするとHはCと共通の頂点をもち、補題よりその頂点を始点とする閉路C_Hを含む。G = C∪C_HであればCとC_Hを合わせた回路がオイラー回路になる。C∪C_HがGに一致しなければ同じことを繰り返していけば最終的にオイラー回路が得られる。■

系2.9 準オイラーグラフ

連結グラフGがオイラー小道をもつための必要十分条件は奇数次数の頂点の個数が0か2であることである。

証明

[⇒]:オイラー小道を

v₀, e₁, v₁, e₂, ⋯, v_n-1, e_n, v_n.

と書くと、始点と終点以外の頂点では入力と出力の相異なる二辺が対になって接続しているので、その頂点の次数は偶数になる。始点と終点が異なる場合、始点は出発時に出力だけ、終点は到着時に入力だけであり、途中に重複してそこを通過するときに入力と出力の相異なる二辺が対になって接続するので、その次数は奇数となる。始点と終点が一致する場合、その次数は偶数となる。
[⇐]:奇数次数の頂点数が2であるとする。奇数次数の二つの頂点u,vを結ぶ新しい辺eを元のグラフGに加えるとG + eは次数が偶数となるのでオイラー回路Cをもつ。このときC - eはGのオイラー小道である。■

無向グラフの例2.1

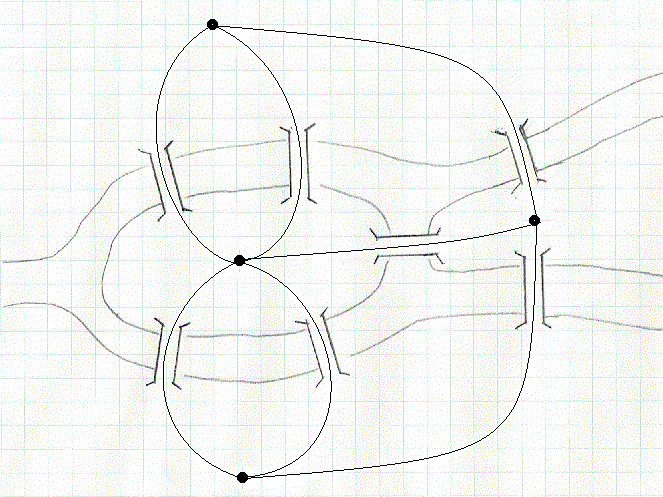
頂点集合V = {a,b,c,d,e,f}、辺集合E = {e₁,e₂,e₃,e₄,e₅,e₆,e₇,e₈,e₉,e₁₀,e₁₁,e₁₂}と写像φが次のように与えられる無向グラフにオイラー小道があるかどうか調べる。

最初にグラフを描く。

graph21.dot:

graph graph21 {
  a;
  b;
  c;
  d;
  e;
  f;
  a -- b [label="e1"];
  a -- c [label="e2"];
  b -- c [label="e3"];
  b -- d [label="e4"];
  c -- e [label="e5"];
  d -- e [label="e6"];
  d -- f [label="e7"];
  e -- f [label="e8"];
  b -- f [label="e9"];
  c -- f [label="e10"];
  a -- f [label="e11"];
  a -- f [label="e12"];
}

$ dot -Tpng graph21.dot -o graph21.png

graph21.png:

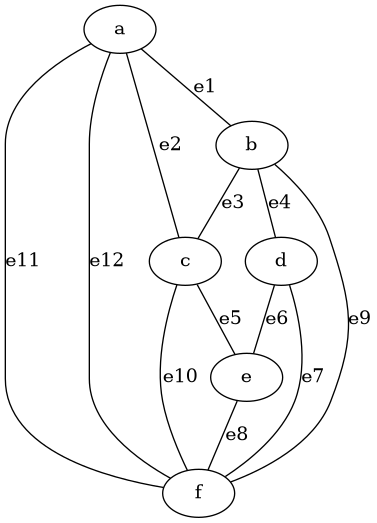
次に次数列を求める。

graph21.rkt:

#lang racket
(require "graph.rkt")
 
(define graph21 (make-graph 'undirected))
(add-vertex! graph21 'a)
(add-vertex! graph21 'b)
(add-vertex! graph21 'c)
(add-vertex! graph21 'd)
(add-vertex! graph21 'e)
(add-vertex! graph21 'f)
(add-edge! graph21 'a 'b 'e1)
(add-edge! graph21 'a 'c 'e2)
(add-edge! graph21 'b 'c 'e3)
(add-edge! graph21 'b 'd 'e4)
(add-edge! graph21 'c 'e 'e5)
(add-edge! graph21 'd 'e 'e6)
(add-edge! graph21 'd 'f 'e7)
(add-edge! graph21 'e 'f 'e8)
(add-edge! graph21 'b 'f 'e9)
(add-edge! graph21 'c 'f 'e10)
(add-edge! graph21 'a 'f 'e11)
(add-edge! graph21 'a 'f 'e12)
 
(define vertices (sort (get-vertices graph21) symbol<?))
(map (λ (v) (cons v (degree graph21 v))) vertices)
(sort (map (λ (v) (degree graph21 v)) vertices) <)

'((a . 4) (b . 4) (c . 4) (d . 3) (e . 3) (f . 6))
'(3 3 4 4 4 6)

次数列は[3,3,4,4,4,6]なのでオイラー小道は存在する。始点をe、終点をdとし、eから小道を伸ばしていく。

e,e₈,f,e₉,b,e₁,a,e₂,c,e₁₀,f,e₁₂,a,e₁₁,f,e₇,d

ここで終点dに到達したのですでに通った辺を除くと

d,e₄,b,e₃,c,e₅,e,e₆,d

という回路が残る。これをつなげばeからdへのオイラー小道になる。

2.3 ケーニヒスベルクの橋

18世紀東プロイセンのケーニヒスベルク(現カリーニングラード)で、町を流れるプルーゲル川にかかる七つの橋すべてをちょうど一度ずつ渡って町を一周する道順はないかということが話題となり、人々はその道順を探すことを楽しんでいたが誰もそれを発見することができなかった。

1736年にオイラーEuler, Leonhard, 1707-1783(Euler, Leonhard, 1707-1783)はケーニヒスベルクの橋の問題を一般化し、それを解く方法に関する論文を発表した。これが現代的なグラフ理論の始まりであるとされている。オイラーの1736年論文では上の定理2.8の必要条件に相当することを証明しているが十分条件を証明していない。この十分条件が証明されたのはドイツの数学者ヒールホルツァーの1873年論文においてである。

図2.10 ケーニヒスベルクの橋

オイラーはケーニヒスベルクの橋の問題を上図のような4頂点/7辺のグラフにオイラー小道があるかどうかの問題に帰着させ、4頂点の次数が[3,3,3,5]であることからオイラー小道が存在しないことを示し、さらに一般のグラフにおけるオイラー小道の存在条件についても考えた。

無向グラフの例2.2

グラフを描く。

graph22.dot:

graph graph22 {
  layout=neato;
  node [shape=point, width=0.1];
  a [pos="0,1!"];
  b [pos="0,0!"];
  c [pos="0,-1!"];
  d [pos="2,0!"];
  a -- b;
  a -- b;
  b -- c;
  b -- c;
  a -- d;
  b -- d;
  c -- d;
}

$ dot -Tpng graph22.dot -o graph22.png

graph22.png:

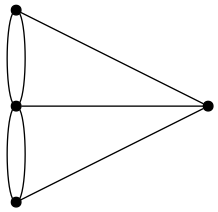
次数列を求める。

graph22.rkt:

#lang racket
(require "graph.rkt")
 
(define graph22 (make-graph 'undirected))
(add-vertex! graph22 'a)
(add-vertex! graph22 'b)
(add-vertex! graph22 'c)
(add-vertex! graph22 'd)
(add-edge! graph22 'a 'b 'e1)
(add-edge! graph22 'a 'b 'e2)
(add-edge! graph22 'b 'c 'e3)
(add-edge! graph22 'b 'c 'e4)
(add-edge! graph22 'a 'd 'e5)
(add-edge! graph22 'b 'd 'e6)
(add-edge! graph22 'c 'd 'e7)
 
(define vertices (sort (get-vertices graph22) symbol<?))
(sort (map (λ (v) (degree graph22 v)) vertices) <)

'(3 3 3 5)

語　　句

歩道ほどう, walk

グラフの頂点vから頂点wへの歩道とは、隣り合った頂点と辺が接続しているような頂点と辺の交互列でvから始まりwで終わるもののこと。

始点してん, start vertex

歩道における先頭の頂点のこと。

終点しゅうてん, end vertex

歩道における末尾の頂点のこと。

小道こみち, trail

辺が重複しない歩道のこと。

道みち, path

頂点が重複しない小道のこと。

閉じたとじた, closed

歩道(小道,道)の始点と終点が一致していることの表現。

開いたひらいた, open

歩道(小道,道)の始点と終点が一致していないことの表現。

回路かいろ, circuit

閉じた小道のこと。

閉路へいろ, cycle

閉じた道のこと。

k-閉路 k-へいろ, k-cycle

長さkの閉路のこと。

奇閉路きへいろ, odd cycle

長さが奇数の閉路のこと。

偶閉路ぐうへいろ, even cycle

長さが偶数の閉路のこと。

連結れんけつ, connected

グラフGにおいて二つの頂点v,wが連結であるとは、vからwへの歩道が存在することである。

連結れんけつ, connected

グラフGが連結であるとは、Gの任意の二頂点が連結であることをいう。

連結成分れんけつせいぶん, connected component

グラフHがグラフGの部分グラフであるとは、V(H)⊆V(G), E(H)⊆E(G)であり、Hの辺の端点がHの頂点であるようなもののことである。

オイラー小道おいらーこみち, Eulerian trail

グラフGのオイラー小道とはGのすべての辺を含む小道のこと。

オイラー回路おいらーかいろ, Eulerian circuit

グラフGのオイラー回路とはGのすべての辺を含む回路のこと。

準オイラーグラフじゅんおいらーぐらふ, semi-Eulerian graph

オイラー小道をもつグラフのこと。

オイラーグラフおいらーぐらふ, Eulerian graph

オイラー回路をもつグラフのこと。

オイラー Euler, Leonhard, 1707-1783

スイス・バーゼルに生まれ、バーゼル大学でヨハン・ベルヌーイに数学を学ぶ。1723年哲学修士号取得。1726年ヨハンの息子ニコラウス・ベルヌーイの後任としてサンクトペテルブルクのロシア帝国科学アカデミーに職を得る。1741～1766年ベルリン・アカデミー在職。1766年サンクトペテルブルクに戻り、1783年そこで生涯を終える。18世紀数学の中心人物で、数学の全部門に数多くの業績を残した。特に数学解析の形式を整備し、物理学や工学へ応用がし易いようにし、これにより19世紀に数学・物理学・工学が飛躍的に発展することとなった。但し、論証の厳密性への関心は薄かった。

This document is licensed under the MIT License.
Copyright (C) 2024 Takeshi Umetani