1. 定義と可視化
著者:梅谷 武
グラフ理論に関する基本的な用語を定義し、グラフのコンピューター上での表現方法について述べる。
作成:2023-04-07
更新:2024-10-25
更新:2024-10-25
定義1.1 グラフ
グラフぐらふ, graph(graph)Gとは頂点ちょうてん, vertex, node(vertex, node)の集合V、辺へん, edge(edge)の集合E、各辺にその端点たんてん, endpoint(endpoint)を対応させる写像φの組G = (V,E,φ)のことである。グラフGの頂点集合をV(G)、辺集合をE(G)と書くことがある。グラフの頂点集合の濃度を位数いすう, order(order)といい、|G|と書く。グラフが有限、無限、可算であるとは、|G|が有限、無限、可算であることをいう。特に断らないときは頂点集合も辺集合も有限であると仮定する。
頂点集合が空のグラフを空グラフくうぐらふ, empty graph(empty graph)という。空グラフの位数は0である。位数が0あるいは1のグラフを自明なグラフじめいなぐらふ, trivial graph(trivial graph)という。特に断らないときはグラフは空でないと仮定する。
辺には有向ゆうこう, directed(directed)と無向むこう, undirected(undirected)の二種類がある。すべての辺に向きがあるグラフを有向グラフゆうこうぐらふ, directed graph(directed graph)といい、すべての辺に向きがないグラフを無向グラフむこうぐらふ, undirected graph(undirected graph)という。有向辺と無向辺が混在するグラフを考える場合もあるがここでは考えない。グラフは有向グラフか無向グラフのどちらかで、単にグラフというときは文脈で有向か無向かを判断する。
無向グラフの写像φはVの冪集合をP(V)で表わすと
| φ : E → P(V), e ↦ φ(e)={v0, v1} |
| φ : E → V×V, e ↦ φ(e)=(v0, v1) |
ループや多重辺をもたないグラフを単純グラフたんじゅんぐらふ, simple graph(simple graph)といい、ループや多重辺をもつグラフを多重グラフたじゅうぐらふ, multigraph(multigraph)という。
辺はその端点に接続せつぞく, connect, incident(connect, incident)するという。辺に接続する二つの端点は隣接りんせつ, adjacent(adjacent)するという。ループの端点は自分自身に隣接する。一つの端点に接続する二つの辺は隣接しているという。
グラフGの各頂点v∈V(G)に対し、それに隣接する頂点集合N(v)⊂V(G)、あるいはそれに誘導されるGの部分グラフG[N(v)]をvの近傍きんぼう, neighbourhood(neighbourhood)という(部分グラフの定義は1.7節参照)。
辺が接続していない頂点を孤立こりつ, isolated(isolated)しているという。
有向グラフは写像φを
に変えれば無向グラフとなる。
| φ' : E → V×V → P(V), e ↦ φ(e)=(v0, v1) ↦ φ'(e)={v0, v1} |
上の定義において写像φの代わりに辺集合をV×VあるいはP(V)の部分集合として定義にすればいいように思えるが、そうすると多重グラフを表現することができない。
第Ⅳ部においてはグラフを可視化するためにGraphvizを用いる。
このため次のように準備しておく。
$ sudo apt update
$ sudo apt upgrade
$ sudo apt install graphviz
頂点集合V = {v1, v2, v3, v4}、辺集合E = {e1, e2, e3, e4}と写像φが次のように与えられる無向グラフ。
| φ(e1) = (v1, v2), φ(e2) = (v1, v2), φ(e3) = (v1, v3), φ(e4) = (v3, v3) |
これをGraphvizで描画するためのdot形式ファイルは次のようになる。
graph11.dot:
graph graph11 {
v1;
v2;
v3;
v4;
v1 -- v2 [label="e1"];
v1 -- v2 [label="e2"];
v1 -- v3 [label="e3"];
v3 -- v3 [label="e4"];
}
dot形式ファイルをpng形式に変換する。
$ dot -Tpng graph11.dot -o graph11.png
graph11.png:
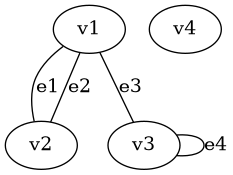

この例においてv1とv2、v1とv3は隣接しており、v3は自分自身に隣接している。v4は孤立している。
v1はe1, e2, e3と接続しており、v2はe1, e2、v3はe3, e4と接続している。
e1, e2, e3とe3, e4は隣接している。
ループをもつ多重グラフである。
頂点集合V = {v1, v2, v3, v4, v5}、辺集合E = {e1, e2, e3, e4}と写像φが次のように与えられる有向グラフ。
| φ(e1) = (v1, v2), φ(e2) = (v1, v3), φ(e3) = (v3, v4), φ(e3) = (v3, v5) |
これをGraphvizで描画するためのdot形式ファイルは次のようになる。
graph12.dot:
digraph graph12 {
v1;
v2;
v3;
v4;
v5;
v1 -> v2 [label="e1"];
v1 -> v3 [label="e2"];
v3 -> v4 [label="e3"];
v3 -> v5 [label="e4"];
}
dot形式ファイルをpng形式に変換する。
$ dot -Tpng graph12.dot -o graph12.png
graph12.png:
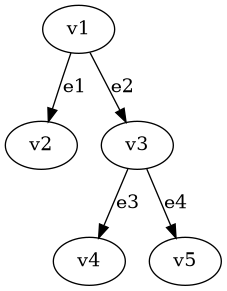

この例においてv1はv2, v3、v3はv1, v4, v5と隣接している。
v1はe1, e2と接続しており、v2はe1、v3はe2, e3, e4、v4はe3、v5はe4と接続している。
e1とe2、e2とe3とe4は隣接している。
ループと多重辺をもたない単純グラフである。
グラフは次の可変構造体graphで表現する。頂点と辺はシンボルで表わす。
- vertices:頂点集合を表わすリスト
- edges:辺集合から頂点対への写像φを表わすハッシュ表
- fibers:写像φの逆像を表わすハッシュ表
グラフアルゴリズムのプロトタイピングにはRacketを用いる。第Ⅳ部において使う機能をライブラリとしてまとめて次に示す。
graph.rkt:
#lang racket
(provide make-graph add-vertex! add-edge! add-weighted-edge!
weight weighted? edge? make-key
get-vertices get-edges get-fibers get-weight get-type
neighbors outdegree indegree degree
incidence-matrix adjacency-matrix adjacency-list
print-graph graph-to-dot)
; type = 'directed or 'undirected
(struct graph (vertices edges fibers weight type) #:mutable)
(define (make-graph type)
(graph '() (make-hash) (make-hash) (make-hash) type))
(define (get-vertices g) (graph-vertices g))
(define (get-edges g) (graph-edges g))
(define (get-fibers g) (graph-fibers g))
(define (get-weight g) (graph-weight g))
(define (get-type g) (graph-type g))
(define (make-key v1 v2 type)
(if (eq? type 'undirected)
(if (symbol<? v1 v2)
(cons v1 v2)
(cons v2 v1))
(cons v1 v2)))
(define (add-vertex! g vertex)
(set-graph-vertices! g (cons vertex (graph-vertices g))))
(define (add-edge! g v1 v2 edge)
(hash-set! (graph-edges g) edge (cons v1 v2))
(let ([type (graph-type g)])
(let* ([key (make-key v1 v2 type)]
[tmp-edges (hash-ref (graph-fibers g) key '())])
(hash-set! (graph-fibers g) key (cons edge tmp-edges)))))
(define (add-weighted-edge! g v1 v2 edge w)
(hash-set! (graph-edges g) edge (cons v1 v2))
(hash-set! (graph-weight g) edge w)
(let ([type (graph-type g)])
(let* ([key (make-key v1 v2 type)]
[tmp-edges (hash-ref (graph-fibers g) key '())])
(hash-set! (graph-fibers g) key (cons edge tmp-edges)))))
(define (weight g edge)
(hash-ref (graph-weight g) edge #f))
(define (weighted? g)
(not (hash-empty? (graph-weight g))))
(define (edge? g v1 v2)
(let ([key (make-key v1 v2 (graph-type g))])
(if (eq? (hash-ref (graph-fibers g) key '()) '())
#f
#t)))
(define (edge-count g v1 v2)
(let ([key (make-key v1 v2 (graph-type g))])
(length (hash-ref (graph-fibers g) key '()))))
(define (neighbors g v)
(let ([type (graph-type g)])
(remove-duplicates (filter (λ (x) x)
(for/list ([key (hash-keys (graph-fibers g))])
(cond
[(eq? type 'directed)
(if (equal? (car key) v)
(cdr key)
#f)]
[(eq? type 'undirected)
(cond
[(equal? (car key) v) (cdr key)]
[(equal? (cdr key) v) (car key)]
[else #f])]))))))
(define (outdegree g v)
(for/sum ([key (hash-keys (graph-fibers g))])
(let* ([edge-list (hash-ref (graph-fibers g) key '())])
(if (equal? (car key) v)
(length edge-list)
0))))
(define (indegree g v)
(for/sum ([key (hash-keys (graph-fibers g))])
(let* ([edge-list (hash-ref (graph-fibers g) key '())])
(if (equal? (cdr key) v)
(length edge-list)
0))))
(define (degree g v)
(let ([type (graph-type g)])
(cond
[(eq? type 'directed)
(+ (outdegree g v) (indegree g v))]
[(eq? type 'undirected)
(for/sum ([key (hash-keys (graph-fibers g))])
(let* ((edge-list (hash-ref (graph-fibers g) key '())))
(cond
[(equal? (car key) v)
(if (equal? (cdr key) v)
(* 2 (length edge-list))
(length edge-list))]
[(equal? (cdr key) v) (length edge-list)]
[else 0])))])))
(define (print-graph g)
(printf "Graph Type: ~a\n" (graph-type g))
(printf "Vertices: ~a\n" (graph-vertices g))
(define arr
(if (eq? (graph-type g) 'undirected)
"--"
"->"))
(printf "Edges:\n")
(if (weighted? g)
(for-each (λ (key)
(printf "~a : ~a ~a ~a : ~a\n"
key
(car (hash-ref (graph-edges g) key))
arr
(cdr (hash-ref (graph-edges g) key))
(hash-ref (graph-weight g) key)))
(hash-keys (graph-edges g)))
(for-each (λ (key)
(printf "~a : ~a ~a ~a\n"
key
(car (hash-ref (graph-edges g) key))
arr
(cdr (hash-ref (graph-edges g) key))))
(hash-keys (graph-edges g))))
(printf "Fibers:\n")
(for-each (λ (key)
(printf "~a ~a ~a : ~a\n"
(car key)
arr
(cdr key)
(hash-ref (graph-fibers g) key)))
(hash-keys (graph-fibers g))))
(define (incidence-matrix g)
(let* ([vertices (sort (get-vertices g) symbol<?)]
[edges (sort (hash-keys (graph-edges g)) symbol<?)]
[rows (length vertices)]
[cols (length edges)])
(define matrix (for/vector ([i rows]) (make-vector cols 0)))
(for ([i rows] [v vertices])
(for ([j cols] [e edges])
(define pair (hash-ref (graph-edges g) e))
(when (or (equal? v (car pair))
(equal? v (cdr pair)))
(vector-set! (vector-ref matrix i) j 1))))
matrix))
(define (adjacency-matrix g)
(let* ([vertices (sort (get-vertices g) symbol<?)]
[n (length vertices)])
(define matrix (for/vector ([i n]) (make-vector n 0)))
(for ([i n] [v1 vertices])
(for ([j n] [v2 vertices])
(define val (edge-count g v1 v2))
(vector-set! (vector-ref matrix i) j val)))
matrix))
(define (adjacency-list g)
(let ([vertices (sort (get-vertices g) symbol<?)])
(for/list ([v vertices])
(cons v (neighbors g v)))))
(define (graph-to-dot g filename)
(call-with-output-file filename
(λ (out)
(define graph-label
(if (eq? (get-type g) 'undirected) "graph" "digraph"))
(define edge-connector
(if (eq? (get-type g) 'undirected) "--" "->"))
(fprintf out "~a G {\n" graph-label)
(for-each
(λ (v)
(fprintf out " ~a [shape=circle];\n" v))
(get-vertices g))
(for-each
(λ (e)
(define edge (hash-ref (get-edges g) e))
(define v1 (car edge))
(define v2 (cdr edge))
(define label (if (weighted? g)
(number->string (weight g e))
(symbol->string e)))
(fprintf out " ~a ~a ~a [label=\"~a\"];\n"
v1 edge-connector v2 label))
(hash-keys (get-edges g)))
(fprintf out "}\n"))
#:exists 'replace))
ソースを見やすくするためにエラー処理は省いている。
頂点集合V = {v1, v2, v3, v4}、辺集合E = {e1, e2, e3, e4}と写像φが次のように与えられる無向グラフ。
| φ(e1) = (v1, v2), φ(e2) = (v1, v2), φ(e3) = (v1, v3), φ(e4) = (v3, v3) |
この無向グラフのデータを作成するには次のようにする。
graph11.rkt:
#lang racket
(require "graph.rkt")
(define graph11 (make-graph 'undirected))
(add-vertex! graph11 'v1)
(add-vertex! graph11 'v2)
(add-vertex! graph11 'v3)
(add-vertex! graph11 'v4)
(add-edge! graph11 'v1 'v2 'e1)
(add-edge! graph11 'v1 'v2 'e2)
(add-edge! graph11 'v1 'v3 'e3)
(add-edge! graph11 'v3 'v3 'e4)
(print-graph graph11)
これを実行するとprint-graphによりグラフ型、頂点リスト、辺-頂点対表、頂点対-辺表が表示される。無向グラフのときは表に書き込むときに頂点対が左項≦右項となるように変換している。
$ racket graph11.rkt
Graph Type: undirected
Vertices: (v4 v3 v2 v1)
Edges:
e1 : v1 -- v2
e4 : v3 -- v3
e2 : v1 -- v2
e3 : v1 -- v3
Fibers:
v1 -- v3 : (e3)
v3 -- v3 : (e4)
v1 -- v2 : (e2 e1)
頂点集合V = {v1, v2, v3, v4, v5}、辺集合E = {e1, e2, e3, e4}と写像φが次のように与えられる有向グラフ。
| φ(e1) = (v1, v2), φ(e2) = (v1, v3), φ(e3) = (v3, v4), φ(e3) = (v3, v5) |
graph12.rkt:
#lang racket
(require "graph.rkt")
(define graph12 (make-graph 'directed))
(add-vertex! graph12 'v1)
(add-vertex! graph12 'v2)
(add-vertex! graph12 'v3)
(add-vertex! graph12 'v4)
(add-vertex! graph12 'v5)
(add-edge! graph12 'v1 'v2 'e1)
(add-edge! graph12 'v1 'v3 'e2)
(add-edge! graph12 'v3 'v4 'e3)
(add-edge! graph12 'v3 'v5 'e4)
(print-graph graph12)
これを実行するとprint-graphによりグラフ型、頂点リスト、辺-頂点対表、頂点対-辺表が表示される。
$ racket graph12.rkt
Graph Type: directed
Vertices: (v5 v4 v3 v2 v1)
Edges:
e1 : v1 -> v2
e4 : v3 -> v5
e2 : v1 -> v3
e3 : v3 -> v4
Fibers:
v1 -> v3 : (e2)
v3 -> v4 : (e3)
v3 -> v5 : (e4)
v1 -> v2 : (e1)
グラフG = (V(G),E(G),φG)とH = (V(H),E(H),φH)が等しいとは
が成り立つことである。しかし、通常はグラフが等しいということを形や名称が違っていても本質的には同じであるというような意味で使っている。これに相当するのがグラフの同型概念である。
| V(G) = V(H), E(G) = E(H), φG = φH |
定義1.2 グラフ同型
グラフG = (V(G),E(G),φG)とH = (V(H),E(H),φH)が同型どうけい, isomorphic(isomorphic)であるとは全単射f:V(G)→V(H), g:E(G)→E(H)| φG(e) = (u,v) ⇔ φH(g(e)) = (f(u),f(v)) |
| G ≅ H |
例えば次の無向グラフは上のgraph11と同型である。
graph11a.dot:
graph graph11a {
0;
1;
2;
3;
0 -- 1 [label="e0"];
0 -- 1 [label="e1"];
0 -- 2 [label="e2"];
2 -- 2 [label="e3"];
}
graph11a.png:
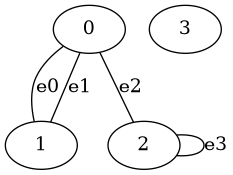

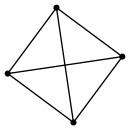
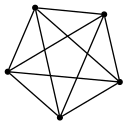
定義1.3 完全グラフ
単純グラフにおいて任意の相異なる二つの頂点が辺で結ばれているとき、これを完全グラフかんぜんぐらふ, complete graph(complete graph)という。位数n(>0)の完全グラフは同型を除いて一意的に定まる。これをKnと書くことにする。 K1からK5までをGraphvizで描いてみる。各頂点を正多角形の頂点に配置するためにneatoレイアウトを指定し、各頂点のrankを同じにする。例えばK3は次のようになる。
k3.dot:
graph K3 {
layout=neato;
node [shape=point];
0 -- 1;
1 -- 2;
2 -- 0;
{ rank=same; 0; 1; 2; }
}

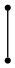

定義1.4 二部グラフ
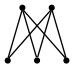
単純グラフG = (V,E,φ)において頂点集合Vが| V = X ∪ Y, X ∩ Y = ∅, X ≠ ∅, Y ≠ ∅ |
| Km,n ≅ Kn,m, n,m>0 |
K2,3をGraphvizで描いてみる。dotレイアウトを指定し、頂点集合を上側と下側に分ける。
k2_3.dot:
graph K2_3 {
layout=dot;
node [shape=point];
0 -- 2;
0 -- 3;
0 -- 4;
1 -- 2;
1 -- 3;
1 -- 4;
rankdir=TB;
{ rank=same; 0; 1; }
{ rank=same; 2; 3; 4; }
}
定義1.5 接続行列
有向グラフGの頂点集合{v1,⋯,vn}と辺集合{e1,⋯,em}について、| mij = |
|
| M(G) := |
|
接続行列の定義は用途により上記と異なる場合がある。
定理1.6 接続行列による同型判定
二つのグラフが同型であることとそれらの頂点リストと辺リストを適当に並べ替えたとき接続行列が一致することは同値である。証明
演習とする。■定義1.7 隣接行列
有向グラフGの頂点集合{v1,⋯,vn}について、| aij := viからvjへ向かう辺の数 |
| A(G) := |
|
無向グラフの隣接行列は各辺が双方向性をもつとしたときの有向グラフとしての隣接行列と定義する。無向グラフの隣接行列は対称行列である。
隣接行列の定義は用途により上記と異なる場合がある。
定理1.8 隣接行列による同型判定
二つのグラフが同型であることとそれらの頂点リストと辺リストを適当に並べ替えたとき隣接行列が一致することは同値である。これは二つのグラフG, Hが同型であることとそれらの隣接行列A(G), A(H)がある置換行列Pにより| A(H) = P∙A(G)∙Pt |
証明
演習とする。■定義1.9 隣接リスト
有向グラフGの頂点集合{v1,⋯,vn}の各頂点viについて、頂点リスト(v1 ⋯ vn)とviを始点とする有向辺の終点リスト(vi1 ⋯)のリスト| ((v11 ⋯) ⋯ (vn1 ⋯)) |
無向グラフの隣接リストは各辺が双方向性をもつとしたときの有向グラフとしての隣接リストと定義する。
定理1.10 隣接リストによる同型判定
二つのグラフが同型であることとそれらの頂点リストと辺リストを適当に並べ替えたとき隣接リストが一致することは同値である。証明
演習とする。■ 接続行列、隣接行列、隣接リストは同型の意味でグラフ構造を決定する情報の異なる表現である。
(incidence-matrix graph11)
(adjacency-matrix graph11)
(adjacency-list graph11)
'#(#(1 1 1 0) #(1 1 0 0) #(0 0 1 1) #(0 0 0 0))
'#(#(0 2 1 0) #(2 0 0 0) #(1 0 1 0) #(0 0 0 0))
'((v1 v3 v2) (v2 v1) (v3 v1 v3) (v4))
(incidence-matrix graph12)
(adjacency-matrix graph12)
(adjacency-list graph12)
'#(#(1 1 0 0) #(1 0 0 0) #(0 1 1 1) #(0 0 1 0) #(0 0 0 1))
'#(#(0 1 1 0 0) #(0 0 0 0 0) #(0 0 0 1 1) #(0 0 0 0 0) #(0 0 0 0 0))
'((v1 v3 v2) (v2) (v3 v4 v5) (v4) (v5))
定義1.12 次数
無向グラフGの頂点vの次数じすう, degree(degree)とはvに接続する辺の数のことである。但しループは二回数えるものとする。vの次数をdeg(v)と書く。有向グラフの次数は方向性を無視したときの無向グラフの次数として定義する。
有向グラフGの頂点vの入次数いりじすう, indegree(indegree)とはvに入る辺の数、出次数でじすう, outdegree(outdegree)とはvから出る辺の数のことである。vの入次数をindeg(v)、出次数をoutdeg(v)と書く。
多重グラフGの頂点vについて|N(v)|とdeg(v)は異なる。
証明
演習とする。■証明
演習とする。■ 例1.1において
| deg(v1) = 3, deg(v2) = 2, deg(v3) = 3, deg(v4) = 0. |
(define vertices (sort (get-vertices graph11) symbol<?))
(map (λ (v) (cons v (degree graph11 v))) vertices)
'((v1 . 3) (v2 . 2) (v3 . 3) (v4 . 0))
例1.2において
| deg(v1) = 2, deg(v2) = 1, deg(v3) = 3, deg(v4) = 1, deg(v5) = 1. |
(define vertices (sort (get-vertices graph12) symbol<?))
(map (λ (v) (cons v (degree graph12 v))) vertices)
'((v1 . 2) (v2 . 1) (v3 . 3) (v4 . 1) (v5 . 1))
次の公式は任意のグラフで成り立つ。
証明
演習とする。■系1.16 奇数次数の頂点数
任意のグラフの奇数次数の頂点数は偶数である。証明
グラフG = (V,E)の辺数|E| = mとし、奇数次数の頂点集合をV1、偶数次数の頂点集合をV2とすると| 2m = |
| = |
| + |
|
定義1.17 正則グラフ
グラフGが正則せいそく, regular(regular)であるとはすべての頂点の次数が等しいことである。グラフGがk-正則k-せいそく, k-regular(k-regular)であるとはすべての頂点の次数がkに等しいことである。 完全グラフKnはn-正則であり、完全二部グラフKm,mはm-正則である。
定義1.18 部分グラフ
グラフG = (V(G),E(G),φG)とH = (V(H),E(H),φH)においてHがGの部分グラフぶぶんぐらふ, subgraph(subgraph)とはV(H)⊆V(G), E(H)⊆E(G)であり、φHがφGのE(H)への制限になっていることであり、H ⊆ Gと書く。H ⊆ GかつH ≠ Gのとき、HはGの真部分グラフしんぶぶんぐらふ, proper subgraph(subgraph)という。H ⊆ Gのとき、GはHの拡大グラフかくだいぐらふ, supergraph(supergraph)であるという。特にH ⊆ GかつV(H) = V(G)のとき、HはGの全域部分グラフぜんいきぶぶんぐらふ, spanning subgraph(spanning subgraph)であるという。
定義1.19 誘導部分グラフ
グラフGの頂点集合Vの空でない部分集合Uに対して、頂点集合をU、辺集合をGの辺で端点がVに含まれるものの集合E(U)とするとG[U] = (U, E(U))はGの部分グラフとなる。これをUから誘導されたGの誘導部分グラフゆうどうぶぶんぐらふ, induced subgraph(induced subgraph)という。[2] J.A.Bondy, U.S.R.Murty, Graph Theory with Applications, NORTH-HOLLAND, 1976
[3] 高橋磐郎, 藤重悟, 離散数学(岩波講座情報数学17), 岩波書店, 1981
[5] 杉原厚吉, データ構造とアルゴリズム, 共立出版, 2001
[6] Susanna S. Epp, Discrete Mathematics with Applications, CENGAGE, 2018
[7] Wikipedia, Glossary of graph theory, Wikimedia Foundation, Inc., 2024
[8] 秋葉拓哉, 岩田陽一, 北川宜稔, プログラミングコンテストチャレンジブック, マイナビ出版, 2012
[9] 安藤清, 土屋守正, 松井泰子, 例題で学ぶグラフ理論, 森北出版, 2013
[10] 宮崎修一, グラフ理論入門 基本とアルゴリズム, 森北出版, 2015
語 句
グラフ ぐらふ, graph頂点と辺から構成される図形。
頂点 ちょうてん, vertex, nodeグラフを構成する要素。
辺 へん, edgeグラフを構成する要素。
端点 たんてん, endpoint辺の両端の点のこと。
位数 いすう, orderグラフの頂点集合の濃度のこと。
空グラフ くうぐらふ, empty graph頂点集合が空のグラフのこと。
自明なグラフ じめいなぐらふ, trivial graph位数が0あるいは1のグラフのこと。
有向 ゆうこう, directed向きがあること。
無向 むこう, undirected向きがないこと。
有向グラフ ゆうこうぐらふ, directed graphすべての辺に向きがあるグラフのこと。
無向グラフ むこうぐらふ, undirected graphすべての辺に向きがないグラフのこと。
ループ るーぷ, loop両端点が一致する辺のこと。
平行 へいこう, parallel同じ端点対に対応する異なる辺の関係性の表現。
多重辺 たじゅうへん, multiple edges同じ端点対に対応する異なる辺のこと。
単純グラフ たんじゅんぐらふ, simple graphループや多重辺をもたないグラフのこと。
多重グラフ たじゅうぐらふ, multigraphループや多重辺をもつグラフのこと。
接続 せつぞく, connect, incident辺とその端点との関係性を表わす表現。
隣接 りんせつ, adjacent辺と辺、頂点と頂点の関係性を表わす表現。
近傍 きんぼう, neighbourhoodグラフのある頂点に隣接する頂点集合、あるいはそれに誘導される部分グラフのこと。
孤立 こりつ, isolated頂点に辺が接続していないこと。
同型 どうけい, isomorphic二つの数学的対象の間に同型写像が存在すること。
同型写像 どうけいしゃぞう, isomorphism二つの数学的対象間の写像で、その存在によりがそれら二つが同型となるようなもの。
完全グラフ かんぜんぐらふ, complete graph任意の相異なる二頂点が辺で結ばれているような単純グラフのこと。
二部グラフ にぶぐらふ, bipartite graph頂点集合を二分割し各部分の頂点は互いに隣接しないようなグラフのこと。
完全二部グラフ かんぜんにぶぐらふ, complete bipartite graph二分割された頂点集合のそれぞれから任意に選んだ頂点対を端点とする辺が存在するような二部グラフのこと。
接続行列 せつぞくぎょうれつ, incidence matrix頂点と辺が隣接しているか否かを示す行列。
隣接行列 りんせつぎょうれつ, adjacency matrix頂点対が隣接しているか否かを示す行列。
隣接リスト りんせつりすと, adjacency list各頂点にそれに隣接している頂点を対応させるリストのこと。
近傍 きんぼう, neighbourhoodグラフのある頂点に隣接する頂点集合のこと。
次数 じすう, degreeグラフの頂点に接続する辺の数のこと。但しループは二回数える。
入次数 いりじすう, indegreeグラフの頂点に入る辺の数のこと。
出次数 でじすう, outdegreeグラフの頂点から出る辺の数のこと。
正則 せいそく, regularすべての頂点の次数が等しいグラフのこと。
k-正則 k-せいそく, k-regularすべての頂点の次数がkに等しいグラフのこと。
部分グラフ ぶぶんぐらふ, subgraphグラフHがグラフGの部分グラフであるとは、Hの頂点はGの頂点、Hの辺はGの辺であるようなもののことである。
真部分グラフ しんぶぶんぐらふ, proper subgraphグラフHがグラフGの真部分グラフであるとはH⊆GかつH≠Gであることをいう。
拡大グラフ かくだいぐらふ, supergraphグラフGがグラフHの拡大グラフであるとは、HがGの部分グラフであることをいう。
全域部分グラフ ぜんいきぶぶんぐらふ, spanning subgraphグラフHがグラフGの全域部分グラフであるとはH⊆GかつV(H)=V(G)であることをいう。
誘導部分グラフ ゆうどうぶぶんぐらふ, induced subgraphグラフGの頂点集合Vの部分集合Uについて、端点がUに属する辺を辺集合とするGの部分グラフG[U]のことをいう。
This document is licensed under the MIT License.
Copyright (C) 2024 Takeshi Umetani